相关试卷
-
1、某考试有20道三项选择题.某同学通过某种手段提前知道了这20道选择题的答案中没有连续相同的选项.试卷下发后,更是发现自己一题也不会做.于是他按照“没有连续相同的选项”猜答案.设其答对第n题的概率是 . 则下列说法正确的是( )A、P(猜对第n+1题|猜对第n题) B、P(猜对第n+1题|猜错第n题) C、 D、全部猜对的概率为
-
2、已知函数的定义域为 , 且在定义域内连续.则下列说法正确的是( )A、设的定义域为D,则D B、设的定义域为D,则D C、若单调,则单调 D、一定存在定义域为的偶函数与奇函数 , 使
-
3、已知在四面体中,为等边三角形,且 , 则与平面所成角正切值的最大值为( )A、 B、 C、 D、
-
4、已知在△ABC中, . P是其内部一点,满足最小.设 . 则t的最小值为( )A、7 B、6 C、 D、
-
5、在函数中,其定义域内每一个x都有一个确定的y值与之对应.而在绘制其反函数或的图象时可能会出现一个x对应多个y值的情况.此时取|y|最小时所对应的y值,并且在此条件下优先取正数.已知函数 , 则其定义域为( )A、 B、 C、 D、
-
6、在等腰直角三角形ABC中, . P为其内部一点,满足 , , 则的正切值为( )A、 B、 C、 D、
-
7、已知椭圆 , 双曲线 . A,B分别为的左,右顶点.过A作直线l与及的右支分别交于点P,Q.若 , 则Q点的横坐标为( )A、 B、 C、5 D、
-
8、现有某个运算器,输入x后有的概率输出 , 有的概率输出 . 将5个这样的运算器串联在一起,初始输入有的概率为1,有的概率为0.则在最后输出为0的条件下,初始输入为1的概率是( )A、 B、 C、 D、
-
9、已知虚数数列 , 则其前4n项和为( )A、 B、 C、 D、
-
10、已知集合A,B,C均为非空集合.若是的充分不必要条件,是的充分不必要条件,则是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
11、某高一学生在周末发展数学兴趣,研究平面向量和解三角形的相关内容时,学习了以下定理,尝试解决一些问题.
塞瓦定理:如图1,设P 为△ABC 三边所在直线外任一点,直线AP,BP,CP 分别交对边所在直线于点D,E,F,则 .
塞瓦定理逆定理:如图1,在△ABC 的三边所在直线BC,CA,AB 上分别各取一点D,E,F,若有 , 则AD,BE,CF 三线共点.
角元塞瓦定理:如图1,设P 为△ABC 三边所在直线外任一点,直线AP,BP,CP 分别交对边所在直线于点D,E,F,则 .
角元塞瓦定理逆定理:如图1,在△ABC 的三边所在直线BC,CA,AB上分别各取一点D,E,F,若有则 , 则AD,BE,CF 三线共点.
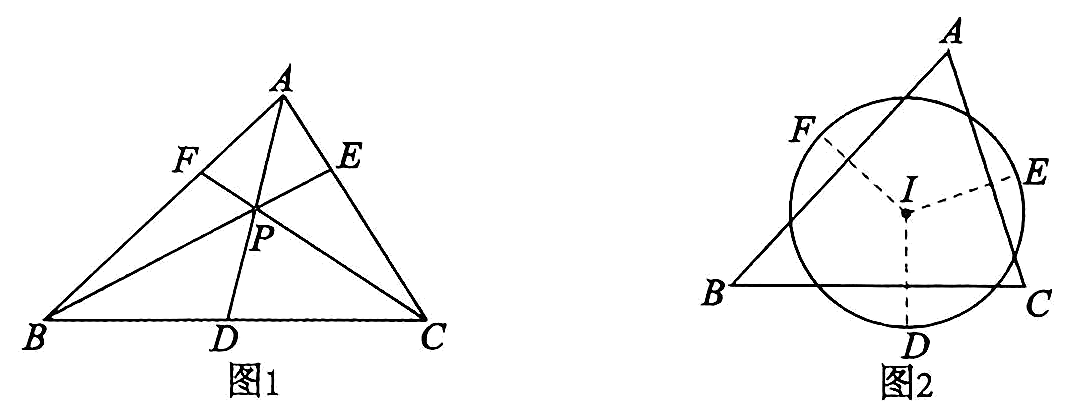 (1)、如图1,在△ABC中,直线AP,BP,CP 分别交对边所在直线于点D,E,F,其中F,D满足 利用塞瓦定理,求点 E 在线段CA 上的位置;若 求(2)、利用塞瓦定理证明角元塞瓦定理;(3)、如图2,过△ABC的内心Ⅰ分别作BC,CA,AB 的垂线,交以Ⅰ为圆心的圆于点D,E,F,利用角元塞瓦定理逆定理证明AD,BE,CF 三线共点.
(1)、如图1,在△ABC中,直线AP,BP,CP 分别交对边所在直线于点D,E,F,其中F,D满足 利用塞瓦定理,求点 E 在线段CA 上的位置;若 求(2)、利用塞瓦定理证明角元塞瓦定理;(3)、如图2,过△ABC的内心Ⅰ分别作BC,CA,AB 的垂线,交以Ⅰ为圆心的圆于点D,E,F,利用角元塞瓦定理逆定理证明AD,BE,CF 三线共点. -
12、如图,在四棱锥中,四边形是边长为4的菱形, , 为等边三角形, , E,F分别是棱 , 的中点.
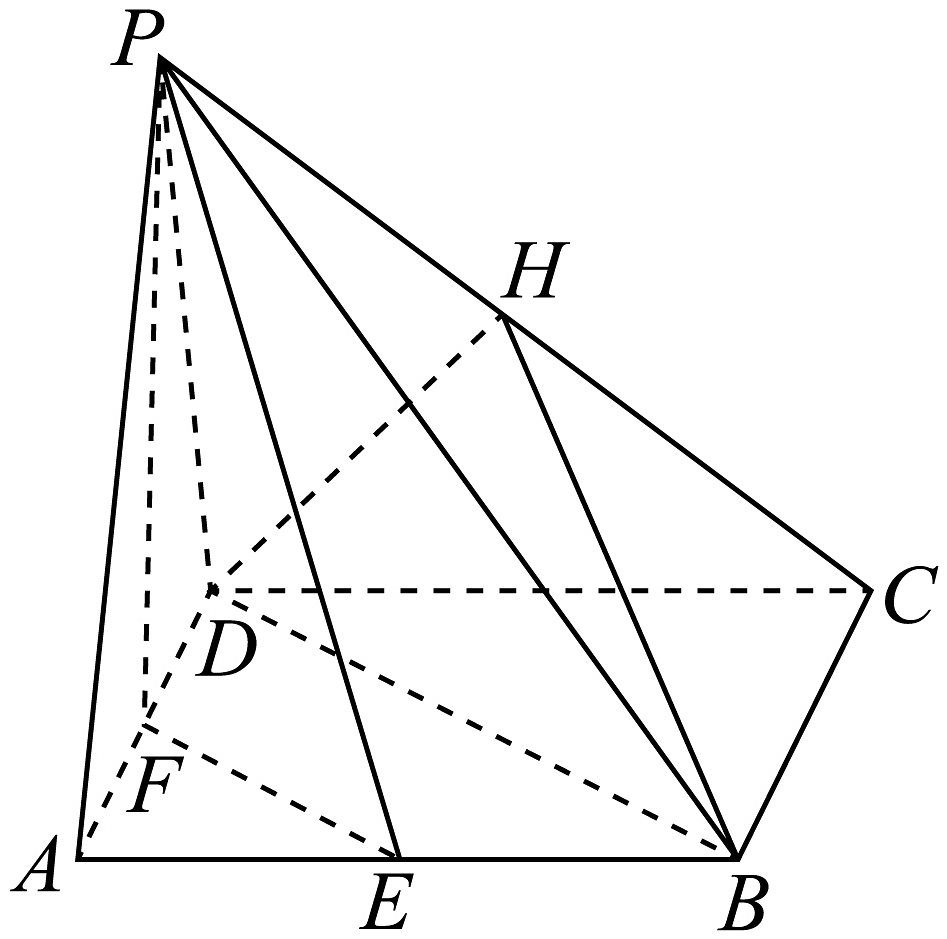 (1)、求四棱锥的体积.(2)、在棱上是否存在点G,使得平面平面?若点G存在,求出的值;若不存在,请说明理由.(3)、若H是棱的中点,求二面角的正弦值.
(1)、求四棱锥的体积.(2)、在棱上是否存在点G,使得平面平面?若点G存在,求出的值;若不存在,请说明理由.(3)、若H是棱的中点,求二面角的正弦值. -
13、在中,内角所对的边分别为 , 且.(1)、求角的大小;(2)、已知为边上一点,若 , 求的长.
-
14、为调查学生体能状况,现从某校高一年级参加体能测试的学生中随机抽取100名学生的体能测试成绩,这组数据均在区间 , 其频率分布直方图如图所示.
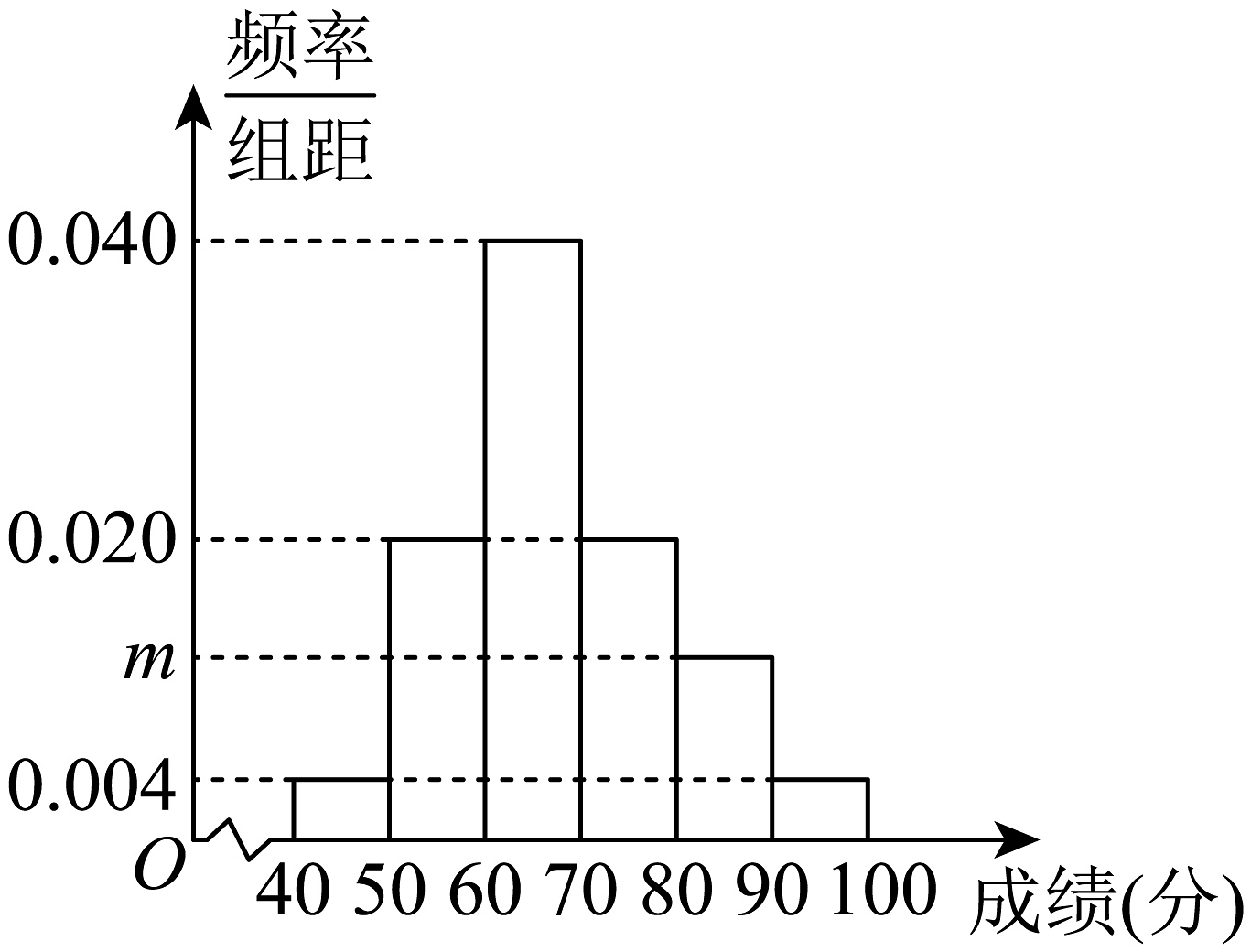 (1)、求m的值;(2)、用组中值估计该校高一学生的平均体能测试成绩;(3)、现用分层抽样的方法从区间 , , 抽取5人,再从抽取的5人中随机抽取2人,求这2人体能测试成绩在的概率.
(1)、求m的值;(2)、用组中值估计该校高一学生的平均体能测试成绩;(3)、现用分层抽样的方法从区间 , , 抽取5人,再从抽取的5人中随机抽取2人,求这2人体能测试成绩在的概率. -
15、已知函数(其中)的最小正周期为.(1)、若 , 求的值;(2)、已知 , 求的值.
-
16、已知一组数据的方差为 , 则数据、、……、的方差为.
-
17、盒子里有2个红球和2个白球,从中不放回地依次取出2个球,设事件“两个球颜色相同”,“第1次取出的是红球”,“第2次取出的是红球”,“两个球颜色不同”.则( )A、与互为对立事件 B、与互斥 C、与相互独立 D、
-
18、设m,n为直线,α,β为平面,则下列结论正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
19、如图1,在等腰梯形中, , 将沿折起,使得点落在点的位置,得到三棱锥 , 如图2所示.则当二面角的平面角的大小为时,三棱锥的外接球的表面积为( )
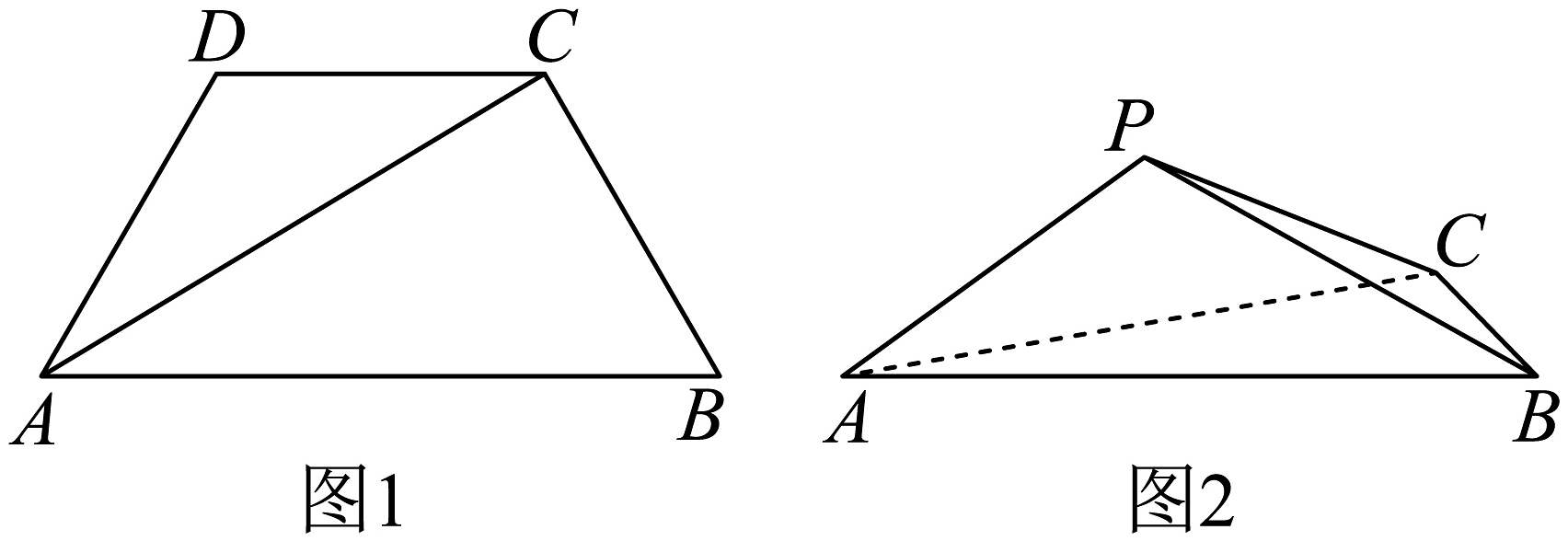 A、 B、 C、 D、
A、 B、 C、 D、 -
20、如图,某实心零部件的形状是正四棱台,已知 , , 棱台的高为 , 现需要对该零部件的表面进行防腐处理,若每平方厘米的防腐处理费用为0.5元,则该零部件的防腐处理费用是( )
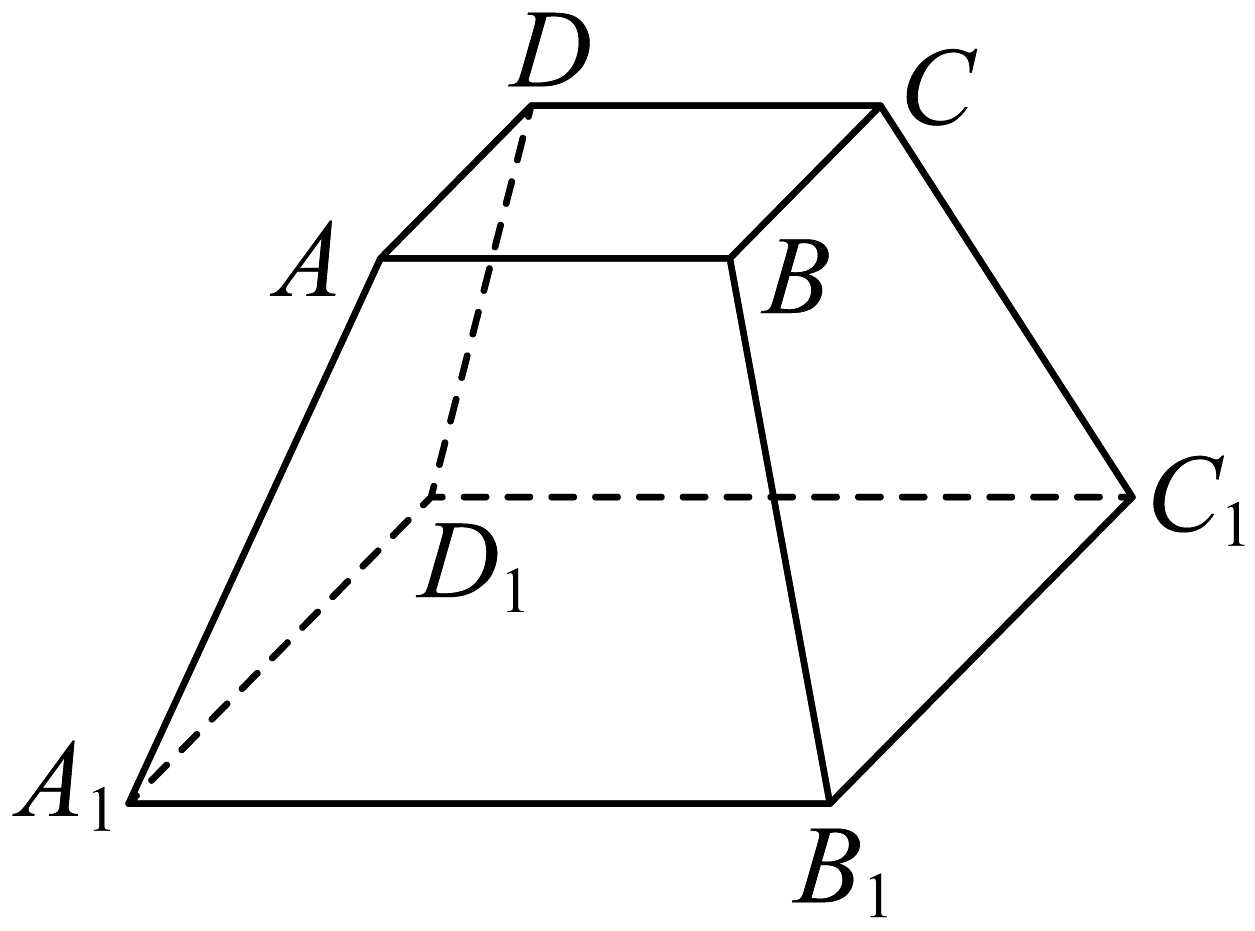 A、160元 B、128元 C、97.5元 D、86.875元
A、160元 B、128元 C、97.5元 D、86.875元