相关试卷
-
1、在三棱锥中,和均是边长为的等边三角形,若 , 则三棱锥的体积为( )A、 B、4 C、 D、
-
2、牛顿冷却定律,即温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的规律.如果物体的初始温度为 , 则经过一定时间t分钟后的温度T满足 , 其中是环境温度,h为常数.现有一个105℃的物体,放在室温15℃的环境中,该物体温度降至75℃大约用时1分钟,那么再经过m分钟后,该物体的温度降至30℃,则m的值约为( )(参考数据: , )A、2.9 B、3.4 C、3.9 D、4.4
-
3、已知是边长为1的正三角形,为中点,且 , 则( )A、 B、 C、 D、
-
4、下列说法不正确的是( )A、对具有线性相关关系的变量 , , 且回归方程为 , 若样本点的中心为 , 则实数的值是 B、若随机变量服从正态分布 , 且 , 则 C、若线性相关系数越接近1,则两个变量的线性相关程度越高 D、一组数据10,10,11,12,12,14,16,19,21,21的第80百分位数为19
-
5、已知函数 , 曲线在点处的切线与直线平行,则实数的值为( )A、 B、 C、 D、1
-
6、设等差数列的前项和为 , 若 , , 则( )A、20 B、18 C、16 D、15
-
7、已知函数.
(1)讨论的单调性;
(2)若 , 且函数只有一个零点,求的最小值.
-
8、在中,点的坐标为 , 边上的中线所在直线的方程为 , 直线的倾斜角为 .(1)、求点的坐标;(2)、过点的直线与轴的正半轴、轴的正半轴分别交于 , 两点,求(为坐标原点)面积的最小值.
-
9、已知函数( , 且)的部分图象如图示.
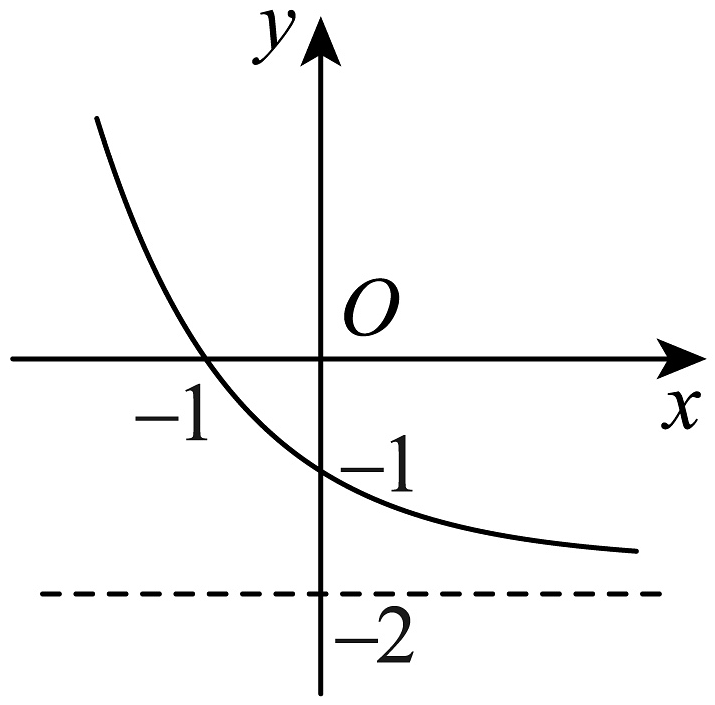 (1)、求的解析式;(2)、若关于x的不等式在上有解,求实数m的取值范围.
(1)、求的解析式;(2)、若关于x的不等式在上有解,求实数m的取值范围. -
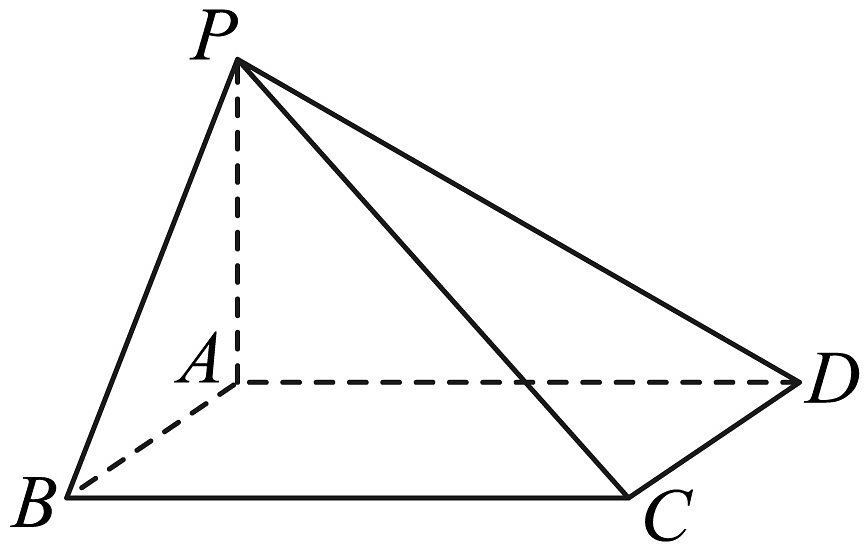
10、在《九章算术》中,将底面为矩形且有一条侧棱与底面垂直的四棱锥称之为阳马.如图,若四棱锥为阳马,侧棱底面 , 且 , , 设该阳马的外接球半径为 , 内切球半径为 , 则 .
-
11、若函数的零点在区间 , 内,则 .
-
12、已知集合 , 则( )A、 B、 C、 D、
-
13、甲、乙、丙、丁、戊5名学生站成一排,记“甲、乙相邻”为事件 , “甲不站在两端”为事件 , 则( )A、 B、 C、 D、
-
14、已知椭圆(且)的焦点为为上的一点,若的周长为18,则椭圆的离心率为 .
-
15、设 , 对任意 , 成立,则该函数称为“级函数”,其中为函数的导数.(1)、判断函数和 , 是否为“级函数”,并说明理由;(2)、记(1)中的“级函数”为 .
①若 , , 使得 , 证明:;
②若 , , 求实数的取值范围.
-
16、某旅游景点统计今年五一期间进入景区的游客人数(单位:千人)如下:
日期
5月1日
5月2日
5月3日
5月4日
5月5日
第天
1
2
3
4
5
参观人数
2.2
2.6
3.1
5.2
6.9
(1)、根据上表数据,判断成对样本数据的线性相关程度,请用样本相关系数加以说明;(若 , 则认为与的线性相关性很强),如果与的线性相关性很强,那么求出关于的经验回归方程;(2)、五一期间景区开放南门、东门和北门供游客出入,游客从南门、东门和北门进入景区的概率分别为 , 且出景区与入景区选择相同门的概率为 , 选择与入景区不同两门的概率各为 . 假设游客从南门、东门、北门出入景点互不影响,现有甲、乙、丙、丁4名游客于5月1日游玩景点,设为4人中从东门出景区的人数,求的分布列、期望及方差.附:参考数据: , , , , .
参考公式:经验回归方程 , 其中 , .
样本相关系数 .
-
17、函数的定义域为 , 如果 , 都有恒成立,那么的图象关于对称.已知 .(1)、讨论的单调性;(2)、当时,
①证明:函数图象关于对称;
②求的值.
-
18、为调查学生喜欢在食堂就餐是否和性别有关,学校随机调研了男女生各100人,经统计得到如下列联表:
男
女
喜欢
80
40
不喜欢
20
60
(1)、依据的独立性检验,判断学生喜欢在食堂就餐是否与性别有关?(2)、为听取学生对食堂的建议,从学生中抽取9人召开座谈会,并给其中3名同学赠送礼品,每人1份(其余人员仅赠送餐券).已知参加座谈会的学生中有且只有4名学生来自高一,求高一这4名学生中得到礼品的人数的分布列和数学期望.0.010
0.005
0.001
6.635
7.879
10.828
附: , 其中
-
19、如图,四棱锥的底面是矩形,平面 , , 为的中点.
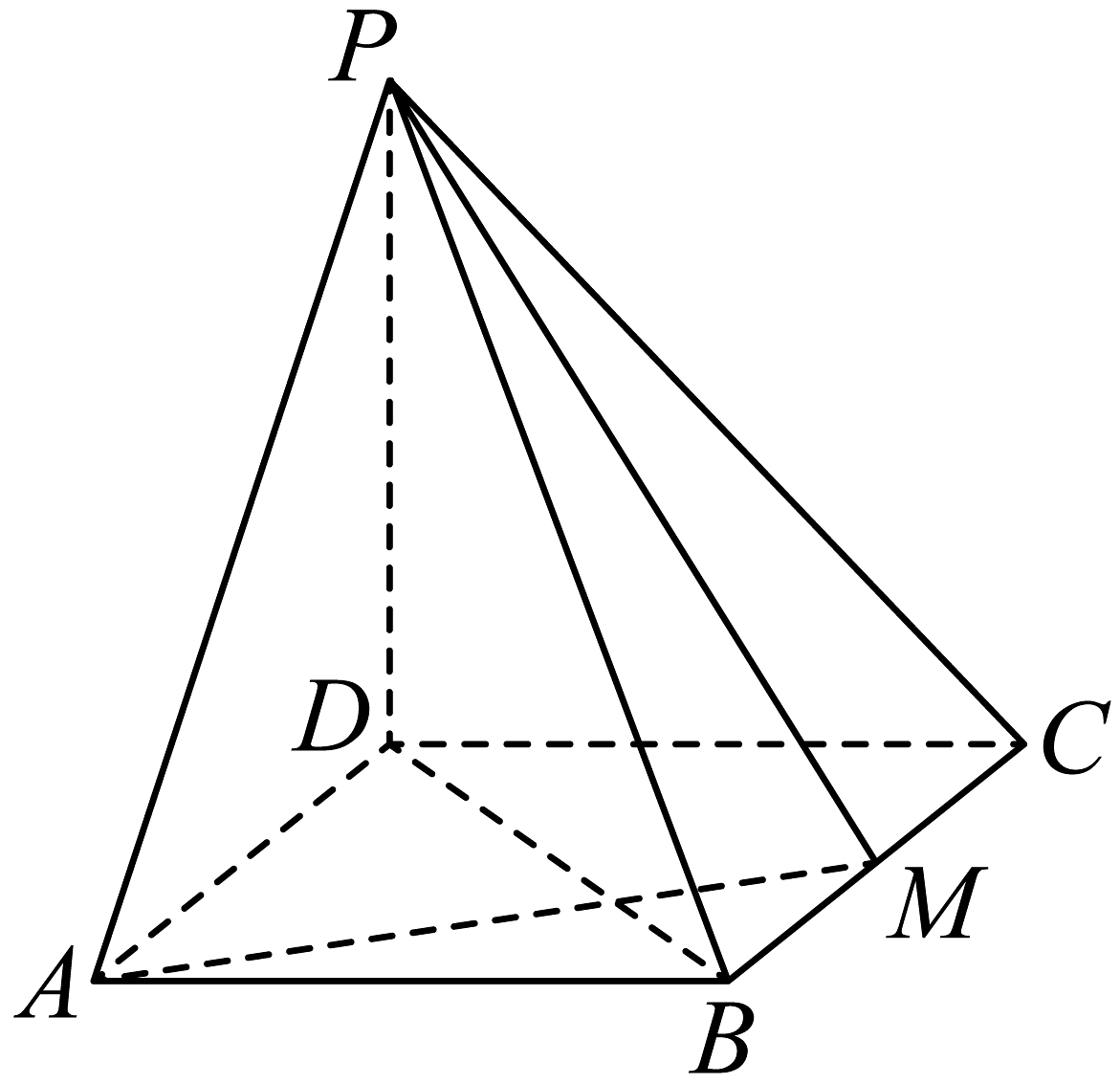 (1)、求证:平面;(2)、求平面与平面夹角的余弦值.
(1)、求证:平面;(2)、求平面与平面夹角的余弦值. -
20、已知 , , 且 . 则满足条件的集合共有个.