相关试卷
-
1、已知函数 , 则下列说法正确的是( )A、是的一个周期 B、的最小值是 C、存在唯一实数 , 使得是偶函数 D、在上有3个极大值点
-
2、已知数列:1,1,2,1,3,5,1,4,7,10,…,其中第1项为1,接下来的2项为1,2,接下来的3项为1,3,5,再接下来的4项为1,4,7,10,依此类推,则( )A、 B、 C、存在正整数m,使得 , , 成等比数列 D、有且仅有4个不同的正整数m,使得
-
3、已知抛物线的焦点为 , 点在上,.若直线与交于另一点 , 则的值是A、 B、 C、 D、
-
4、在直角梯形中, , , , , 是的中点,则
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、如图,在圆柱内有一个球O,该球与圆柱的上,下底面及母线均相切.若 , 则圆柱的表面积为( )
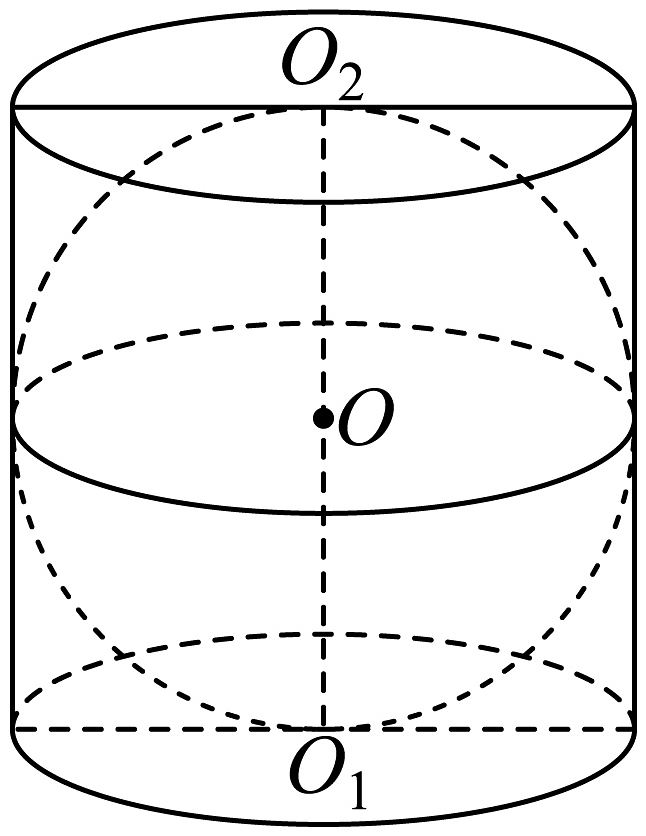 A、 B、 C、 D、
A、 B、 C、 D、 -
6、马林·梅森(MarinMersenne,1588-1648)是17世纪法国著名的数学家和修道士,也是当时欧洲科学界一位独特的中心人物.梅森在欧几里得、费马等人研究的基础上对作了大量的计算、验证工作,人们为纪念梅森在数论方面的这一贡献,将形如(其中是素数)的素数,称为梅森素数.在不超过40的素数中,随机选取两个不同的数,至少有一个为梅森素数的概率是( )A、 B、 C、 D、
-
7、设集合 , 集合 , 则( )A、 B、 C、 D、
-
8、如图,在四棱锥中,底面是边长为1的正方形,底面 , , 点为线段上的动点(不包括端点),则下列结论正确的是( )
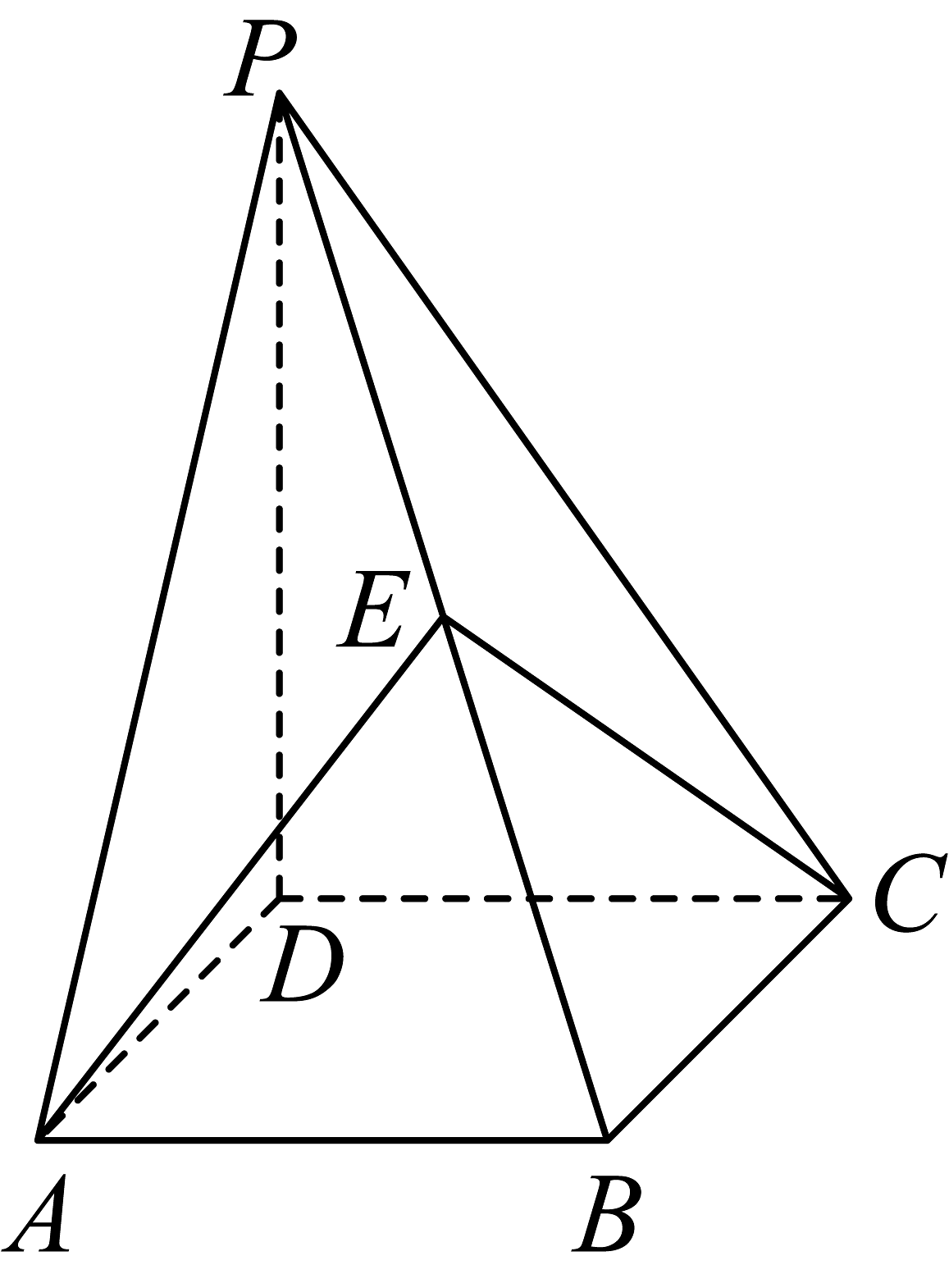 A、该四棱锥的体积为 B、一定存在点 , 使平面 C、一定存在点 , 使平面 D、的最小值为
A、该四棱锥的体积为 B、一定存在点 , 使平面 C、一定存在点 , 使平面 D、的最小值为 -
9、甲、乙、丙三人相互做传球训练,第1次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人.(1)、求次传球后球在甲手中的概率;(2)、求次传球后球在乙手中的概率;(3)、已知:若随机变量服从两点分布,且 , , 则 , 记前n次传球后(即从第1次传球到第次传球后)球在甲手中的次数为 , 求.
-
10、如图,和所在平面垂直,且 , , 求:
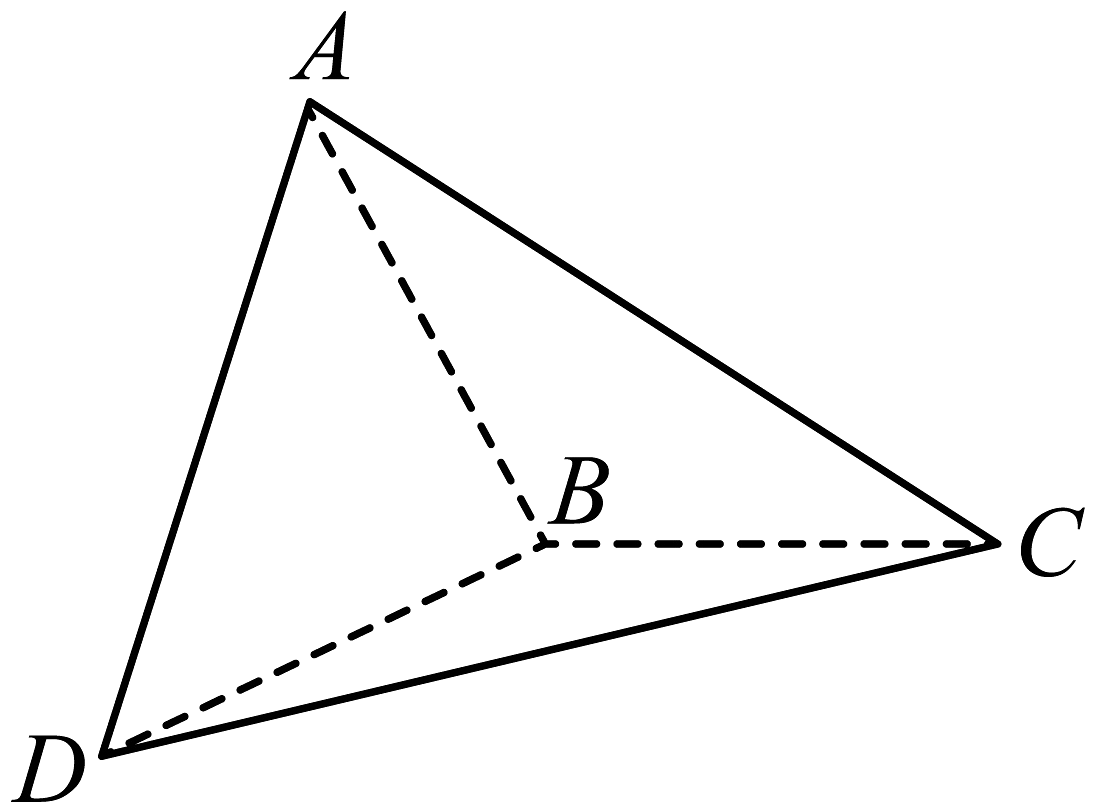 (1)、直线与平面所成角的大小;(2)、平面和平面夹角的余弦值.
(1)、直线与平面所成角的大小;(2)、平面和平面夹角的余弦值. -
11、已知某商品进价为a元/件,根据以往经验,当售价是元/件时,可卖出c件,市场调查表明,当售价下降10%时,销量可增加40%.现决定一次性降价,为获得最大利润,售价应定为元/件.(用含a,b的式子表示)
-
12、已知定义在上的函数满足:对 , 都有 , 则对于 , , 下式成立的有( )A、 B、 C、 D、
-
13、设随机变量 , 记 , , 下列说法正确的是( )A、当k由0增大到n时,先增后减,在某一个(或两个)k值处达到最大.二项分布当时是对称的,当时向右偏倚,当时向左偏倚 B、如果为正整数,当且仅当时,取最大值 C、如果为非整数,当且仅当k取的整数部分时,取最大值 D、
-
14、展开式中第4项的二项式系数为( )A、 B、1120 C、56 D、70
-
15、已知函数有两个极值点.(1)、求实数的取值范围;(2)、记两个极值点分别为 , , 证明:.
-
16、为数列的前n项和,已知 .(1)、求的通项公式;(2)、设 , 求数列的前n项和 .
-
17、2022年北京冬奥会开幕式中,当《雪花》这个节目开始后,一片巨大的“雪花”呈现在舞台中央,十分壮观.理论上,一片雪花的周长可以无限长,围成雪花的曲线称作“雪花曲线”,又称“科赫曲线”,是瑞典数学家科赫在1904年研究的一种分形曲线.如图是“雪花曲线”的一种形成过程:从一个正三角形开始,把每条边分成三等份,然后以各边的中间一段为底边分别向外作正三角形,再去掉底边,重复进行这一过程
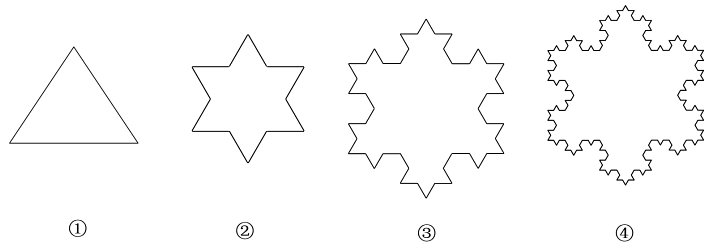
若第1个图中的三角形的周长为1,则第n个图形的周长为;若第1个图中的三角形的面积为1,则第n个图形的面积为.
-
18、为弘扬志愿者精神,某校举行“乐于助人”服务活动,现安排甲,乙等4人到三个不同地方参加活动,每个地方至少1人,若甲和乙不能去同一个地方,则不同的安排方式有种.
-
19、已知则( )A、 B、 C、 D、
-
20、已知双曲线C:的左、右焦点分别为 , , 直线经过 , 且与C交于A,B两点,若 , , 则的离心率为( )A、 B、 C、 D、