相关试卷
-
1、已知集合 , , 则( )A、 B、 C、 D、
-
2、椭圆 , 椭圆 , 若 , 则椭圆与椭圆为相似椭圆,其中为相似比.已知椭圆的长轴长为4,且过点为椭圆上异于其左,右顶点的任意一点.(1)、若 , 求椭圆的标准方程;(2)、在(1)的条件下,若与椭圆有且只有一个公共点的直线恰好相交于点 , 直线的斜率分别为 , 求的值;(3)、若 , 设直线与椭圆交于点 , 直线与椭圆交于点 , 求的值.
-
3、如图,在四棱锥中,平面平面 , 底面为直角梯形,//.在平面内过作// , 交于 , 连.
 (1)、求证:平面平面;(2)、求平面与平面所成角的余弦值;(3)、点是平面上的动点,若直线与平面所成的角为30°,求的最小值.
(1)、求证:平面平面;(2)、求平面与平面所成角的余弦值;(3)、点是平面上的动点,若直线与平面所成的角为30°,求的最小值. -
4、已知双曲线 , 直线与双曲线交于两点.(1)、若关于点对称,求直线的方程;(2)、若直线过 , 且都在双曲线的左支,求直线的斜率的取值范围.
-
5、如图,在三棱柱中, , , , 、分别是、的中点.
 (1)、求的长;(2)、求与所成角的余弦值.
(1)、求的长;(2)、求与所成角的余弦值. -
6、古希腊著名数学家阿波罗尼斯发现:若动点与两个定点的距离之比为常数且 , 则点的轨迹是圆.后来,人们以他的名字命名这个圆,称为阿波罗尼斯圆,简称阿氏圆.已知 , 圆上的点满足.(1)、求圆的标准方程;(2)、若直线过原点,且直线与圆相切,求直线的方程.
-
7、如图,在正四棱柱中, , 顶点在平面内,其余顶点在的同侧,顶点到平面的距离分别为、 , 则顶点到平面的距离为.

-
8、直线的倾斜角为.
-
9、在空间直角坐标系中,已知点 , 则下列结论正确的是( )A、若 , 则 B、是直线的一个方向向量 C、 D、在上的投影向量为
-
10、自19世纪之后,折纸艺术与自然科学结合到了一起,它开始在西方成为教育教学和科学研究的工具.随着折纸过程中的数学之迷被解开,折纸发展成为了现代几何学的一个分支.现有一张半径为 , 圆心为的圆形纸片,在圆内选定一点且.将圆形纸片翻折一角,使圆周正好过点 , 把纸片展开后,留下一条折痕,折痕上到两点距离之和最小的点为.如此反复,就能得到越来越多的折痕,设点的轨迹为曲线 , 线段的中点为 , 在上任取一点 , 则的最小值是( )A、 B、 C、 D、
-
11、已知二面角 , 、两点在棱上,直线分别在这个二面角的两个半平面内,且都垂直于.已知 , 则二面角的大小是( )A、30° B、60° C、120° D、150°
-
12、对于方程 , 表示的曲线 , 下列说法正确的是 ( )A、曲线只能表示圆、椭圆或双曲线 B、若为负角,则曲线为双曲线 C、若为正角,则曲线为椭圆 D、若为椭圆,则曲线的焦点在轴上
-
13、已知直线 , 直线 , 则下列结论正确的是( )A、直线的斜率 B、直线过定点 C、若 , 则或 D、若 , 则或
-
14、设圆和圆交于两点,则弦的长度为( )A、4 B、 C、2 D、1
-
15、设为空间的一个基底,若向量 , 则向量在基底下的坐标为.若向量以为基底时的坐标为 , 则可以为基底时的坐标为( )A、 B、 C、 D、
-
16、双曲线的渐近线方程为( )A、 B、 C、 D、
-
17、设是直线的方向向量,是平面的法向量,则( )A、或 B、或 C、 D、
-
18、已知椭圆上有两个不同点 , 关于直线对称.(1)、记直线与线段的交点为.
(i)求证:为定值;
(ii)求的坐标(用来表示).
(2)、求面积的最大值(为坐标原点). -
19、如图,已知四棱锥的底面为矩形, , , 顶点在底面的正投影为的中点.
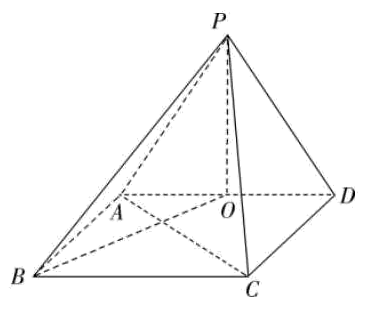 (1)、求证:直线平面;(2)、若平面与平面的交线为 , ,
(1)、求证:直线平面;(2)、若平面与平面的交线为 , ,(i)求证:直线;
(ii)求与平面所成角的大小.
-
20、已知圆过点 , , 且圆心在直线上.(1)、求圆的标准方程;(2)、问是否存在满足以下两个条件的直线:
①斜率为1;②直线被圆截得的弦为 , 以为直径的圆过原点.若存在这样的直线,请求出其方程;若不存在,请说明理由.