相关试卷
-
1、如图,在四棱锥中,底面 , 平面 , .
 (1)、证明:平面.(2)、若 , , 且直线与直线所成角的正切值为 , 求二面角的余弦值.
(1)、证明:平面.(2)、若 , , 且直线与直线所成角的正切值为 , 求二面角的余弦值. -
2、函数的部分图象如图所示,则下列说法正确的是( )
 A、 B、的一个单调递增区间为 C、函数的图象关于点对称 D、若函数在上没有零点,则
A、 B、的一个单调递增区间为 C、函数的图象关于点对称 D、若函数在上没有零点,则 -
3、下列命题说法正确的有( )A、已知直线:与直线: , 若 , 则或 B、点关于直线的对称点的坐标为 C、直线过定点 D、过点且在轴,轴上的截距相等的直线方程为
-
4、在中,点是边上一点,若 , 则的最小值为( )A、 B、 C、 D、7
-
5、已知直线恒过点 , 圆 , 则“直线的斜率为”是“直线与圆相切”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件
-
6、为了研究我市甲、乙两个智能手机专卖店的销售状况,厂家统计了去年4月到9月甲、乙两店每月的营业额(单位:万元),得到如图所示的折线图.根据两店的营业额折线图可知,下列说法错误的是( )
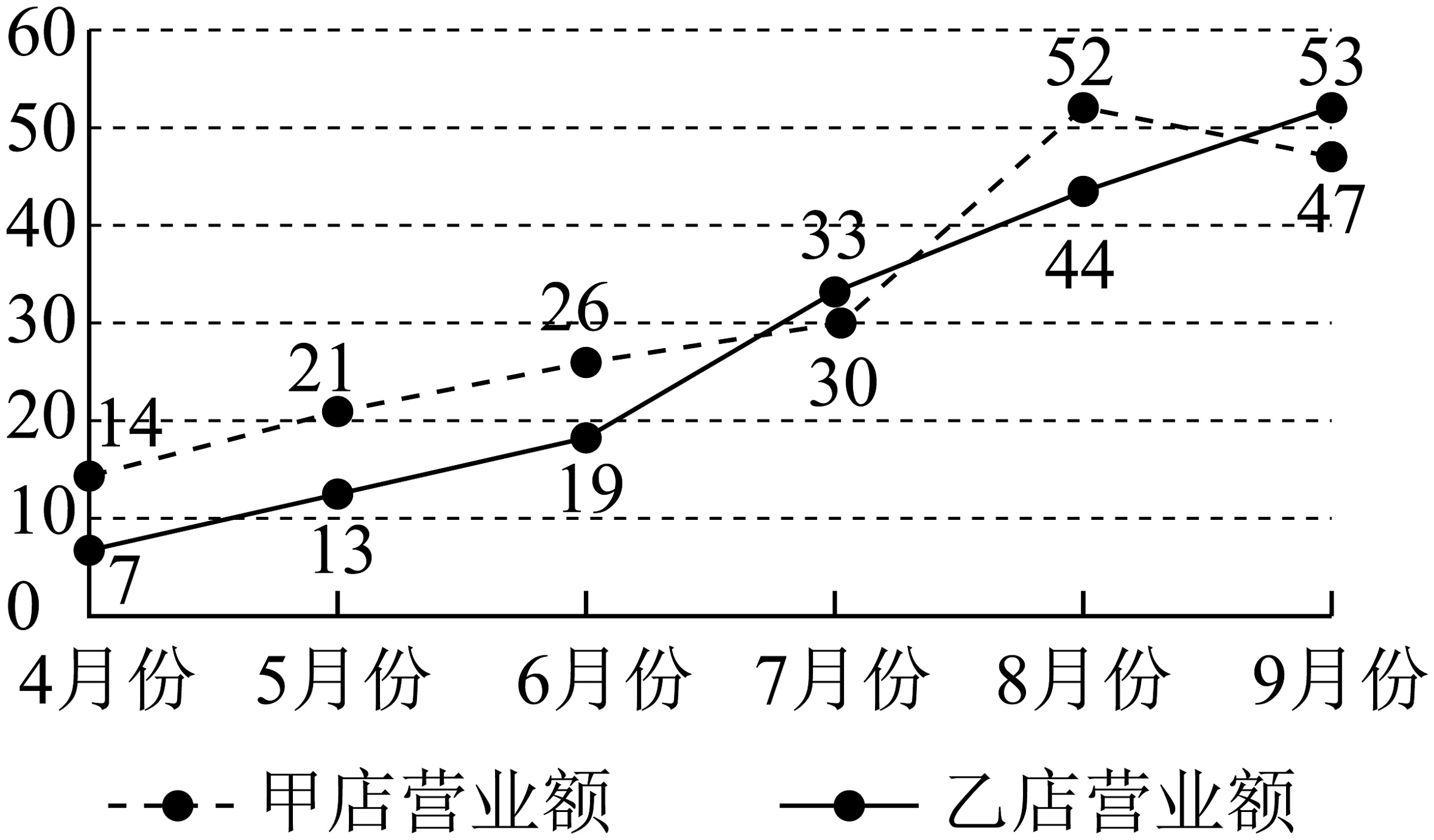 A、甲店月营业额的平均值在内 B、乙店月营业额总体呈上升趋势 C、7、8、9月份的总营业额甲店比乙店少 D、乙店的月营业额极差小于甲店的月营业额极差
A、甲店月营业额的平均值在内 B、乙店月营业额总体呈上升趋势 C、7、8、9月份的总营业额甲店比乙店少 D、乙店的月营业额极差小于甲店的月营业额极差 -
7、已知圆的面积被直线平分,圆 , 则圆与圆的位置关系是( )A、外离 B、相交 C、内切 D、外切
-
8、在三棱柱中,分别是的中点, , 则( )A、 B、 C、 D、
-
9、已知直线与垂直,则( )A、0 B、0或 C、 D、0或
-
10、已知集合 , 则( )A、 B、 C、 D、
-
11、已知函数(为常数,).(1)、讨论函数的奇偶性;(2)、若方程在上有实根,求实数的取值范围.
-
12、已知幂函数 , 且.(1)、求函数的解析式;(2)、若均为正数且 , 求的最小值.
-
13、(1)解不等式
(2)解不等式
-
14、已知关于x的不等式(ax﹣a2﹣4)(x﹣4)>0的解集为A,且A中共含有n个整数,则当n最小时实数a的值为 .
-
15、已知f(x+)=x2+ , 则函数f(x)= .
-
16、若函数(且)经过的定点是P,则P点的坐标是 .
-
17、已知函数的定义域为R, , 则( )A、 B、 C、是奇函数 D、是偶函数
-
18、(多选)以下关于数的大小的结论正确的是( )A、 B、 C、 D、
-
19、下列函数中,既是偶函数又在区间单调递增的是( )A、 B、 C、 D、
-
20、已知不等式的解集为 , 则实数( )A、 B、0 C、1 D、2