相关试卷
-
1、函数为定义在上的偶函数,则实数等于( )A、 B、1 C、0 D、无法确定
-
2、已知 , 则函数的最小值为A、﹣1 B、0 C、1 D、2
-
3、命题: , , 则为( )A、 , B、 , C、 , D、 ,
-
4、已知直线及圆.(1)、求证:直线过定点,并求出圆心到直线距离最大时的值;(2)、若直线与圆相交于、两点,且弦的长为 , 求的值.
-
5、如图所示,在几何体中,四边形和均为边长为的正方形, , 底面 , 、分别为、的中点,.
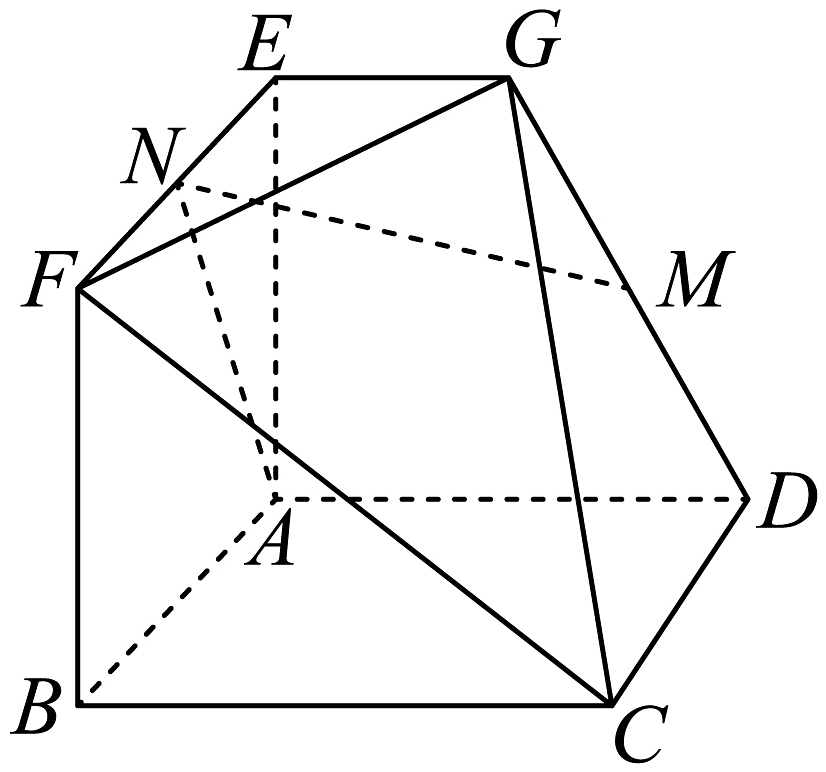 (1)、求证:平面;(2)、求点到平面的距离.
(1)、求证:平面;(2)、求点到平面的距离. -
6、求经过直线与直线的交点 , 且分别满足下列条件的直线方程:(1)、与直线平行;(2)、与直线垂直.
-
7、已知实数、满足 , 则的取值范围为.
-
8、直线关于直线对称的直线的方程为.
-
9、已知椭圆的标准方程为 , 则椭圆的离心率是.
-
10、已知直线与圆相交于、两点,下列说法正确的是( )A、若圆关于直线对称,则 B、的最小值为 C、若、、、(为坐标原点)四点共圆,则 D、当时,对任意 , 曲线恒过直线与圆的交点
-
11、已知直线的倾斜角等于 , 且经过点 , 则下列结论中正确的是( )A、的一个方向向量为 B、在轴上的截距等于 C、与直线垂直 D、点到直线上的点的最短距离是1
-
12、在空间直角坐标系中,点 , , , 下列结论正确的有( )A、 B、向量与的夹角的余弦值为 C、点关于轴的对称点坐标为 D、直线的一个方向向量
-
13、已知是椭圆的两个焦点,是椭圆上任意一点,过引的外角平分线的垂线,垂足为 , 则与短轴端点的最近距离为( )A、 B、 C、 D、
-
14、如图所示,正方体的棱长为1,点 , , 分别为 , , 的中点,则下列说法正确的是( )
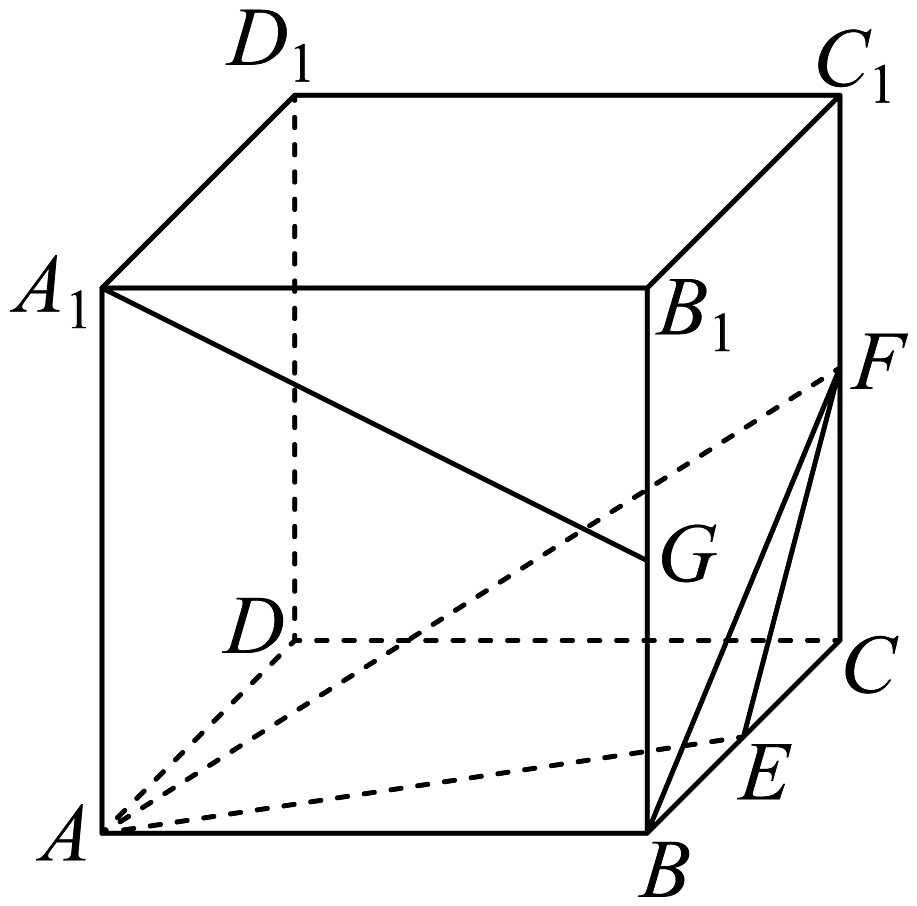 A、直线与直线垂直 B、三棱锥的体积为 C、直线与平面平行 D、直线与平面所成的角为
A、直线与直线垂直 B、三棱锥的体积为 C、直线与平面平行 D、直线与平面所成的角为 -
15、方程表示椭圆的充要条件是( )A、 B、 C、 D、或
-
16、空间四边形中, , , , 点在上,且为中点,为中点,则等于( )A、 B、 C、 D、
-
17、若点在圆的内部,则实数的取值范围是( )A、 B、 C、 D、
-
18、已知函数(1)、若 , 判断的奇偶性,求的最大值;(2)、若的最大值为 , 求的最小值.
-
19、某租赁公司,购买了一辆小型挖掘机进行租赁.据市场分析,该小型挖掘机的租赁利润(单位:万元)与租赁年数的关系为.(1)、该挖掘机租赁到哪几年时,租赁的利润超过万元?(2)、该挖掘机租赁到哪一年时,租赁的年平均利润最大?
-
20、设函数 , 其图像过点(1)、求出的解析式;(2)、判断函数在上的单调性,并用定义证明.