相关试卷
-
1、记的内角的对边分别为.已知为边的中点,且.(1)、求证:;(2)、若 , 求的面积.
-
2、已知函数 , 则下列结论正确的是( )A、是周期为的奇函数 B、的图象关于点对称 C、在上单调递增 D、的值域是
-
3、已知是奇函数.(1)、求实数a的值;(2)、判断函数的单调性,并用定义证明之;(3)、解关于t的不等式 .
-
4、某租赁公司有750辆电动汽车供租赁使用,管理这些电动汽车的费用是每日元.根据调查发现,若每辆电动汽车的日租金不超过90元,则电动汽车可以全部租出;若超过90元,则每超过1元,租不出去的电动汽车就增加3辆.设每辆电动汽车的日租金为元(),用(单位:元)表示出租电动汽车的日净收入.(日净收入等于日出租电动汽车的总收入减去日管理费用)
(1)求关于的函数解析式;
(2)试问当每辆电动汽车的日租金为多少元时?才能使日净收入最多,并求出日净收入的最大值.
-
5、已知集合 , , 全集 .(1)、当时,求;(2)、若是成立的充分不必要条件,求实数的取值范围.
-
6、函数的定义域为 .
-
7、已知不等式的解集为 , 下列说法正确的是( )A、; B、 , 2是方程的两个实数根; C、; D、不等式的解集为或 .
-
8、已知幂函数的图象过点 , 若 , 则的取值范围为( )A、 B、 C、 D、
-
9、设 , 且 , 则的最小值为( )A、4 B、5 C、 D、
-
10、函数的零点所在的区间是( )A、 B、 C、 D、
-
11、命题“”的否定是( )A、 B、 C、 D、
-
12、设全集是实数集 , , , 则等于 ( )A、 B、 C、 D、
-
13、类似平面解析几何中的曲线与方程,在空间直角坐标系中,可以定义曲面(含平面)的方程,若曲面和三元方程之间满足:①曲面上任意一点的坐标均为三元方程的解;②以三元方程的任意解为坐标的点均在曲面上,则称曲面的方程为 , 方程的曲面为 . 已知曲面的方程为 . 如图,该曲面可视为平面中某一支曲线绕轴旋转一周所得的旋转面.
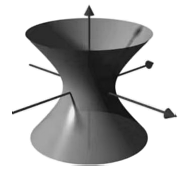 (1)、请写出平面截曲面所得交线是什么曲线;(2)、已知过曲面上任意一点,有且仅有两条直线,使得它们均在曲面上.若直线过曲面上一点 , 以为方向向量.
(1)、请写出平面截曲面所得交线是什么曲线;(2)、已知过曲面上任意一点,有且仅有两条直线,使得它们均在曲面上.若直线过曲面上一点 , 以为方向向量.①求证:直线在曲面上;
②若直线在曲面上,且过点 , 求异面直线与所成角的余弦值.
-
14、在如图所示的试验装置中,两个正方形框架 , 的边长都是1,且它们所在平面互相垂直,活动弹子分别在正方形对角线和上移动,且和的长度保持相等,记 , 活动弹子在上移动.
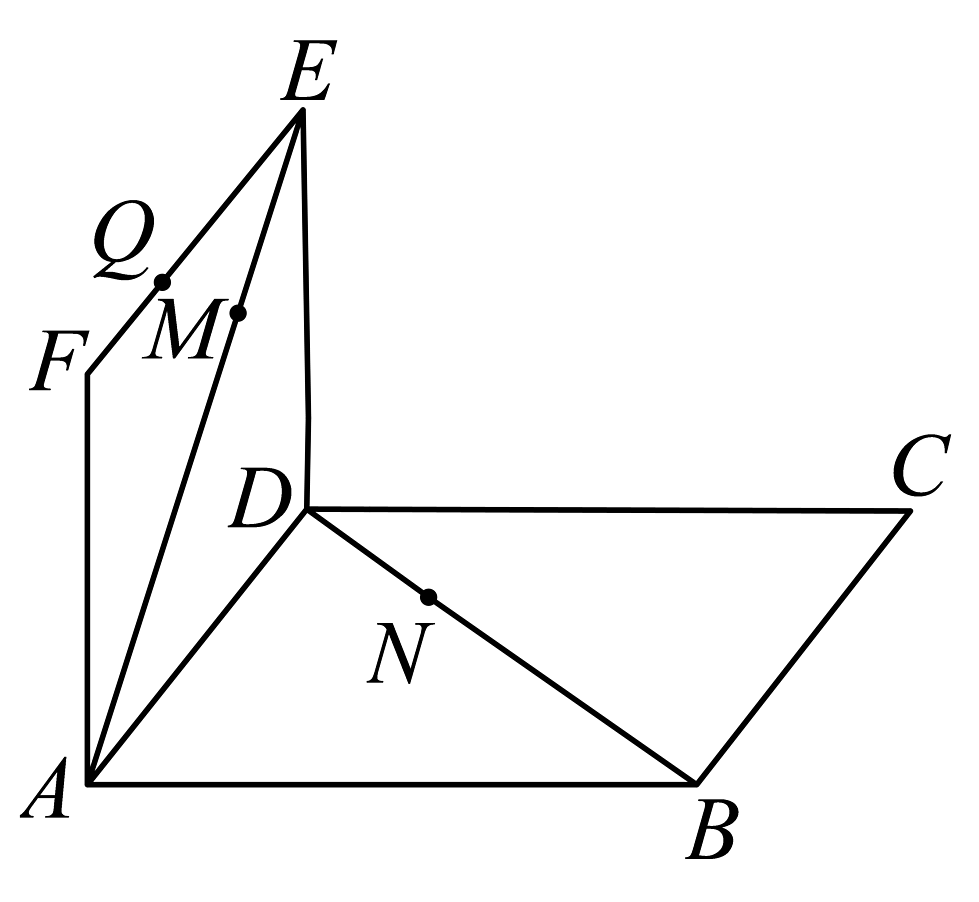 (1)、求证:直线平面;(2)、a为何值时,的长最小?(3)、为上的点,求与平面所成角的正弦值的最大值.
(1)、求证:直线平面;(2)、a为何值时,的长最小?(3)、为上的点,求与平面所成角的正弦值的最大值. -
15、记的内角的对边分别为 , 已知 , 外接圆的半径为R.(1)、求外接圆的面积;(2)、圆经过 , 且与圆关于直线对称,圆被直线截得弦长为8,求直线的方程.
-
16、设直线l的方程为(1)、求证:无论a为何值,直线l必过一定点P;(2)、若直线l分别与x轴正半轴,y轴正半轴交于A,B,当面积最小时,求的周长;(3)、当直线l在两坐标轴上的截距均为整数且斜率为正值时,求直线l的方程.
-
17、已知点 , 设 .(1)、求在方向上的投影向量(用坐标表示);(2)、求 .
-
18、已知P为上的点,过点P作圆O:的切线,切点为M、N,若使得的点P有8个,则m的取值范围是.
-
19、设直线经过点是它的一个方向向量,是直线上任意一点,则向量与共线,根据向量共线的充要条件,存在唯一的实数 , 使 , 即 , 所以 , 我们把上式称为直线的参数方程.若直线的参数方程为(为参数),则其倾斜角为 .
-
20、已知空间向量 , , 共面,则实数的值为 .