相关试卷
-
1、已知单位向量 , 的夹角为 , 则下列结论正确的有( )A、 B、在方向上的投影向量为 C、若 , 则 D、若 , 则
-
2、已知 , 则=( )A、 B、 C、 D、
-
3、设 , 都是不等于1的正数,则“”是“”的( )A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件
-
4、在复平面内,复数对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
5、已知集合 , , 则的真子集的个数为( )A、8 B、7 C、16 D、15
-
6、已知线段是圆的一条动弦, , 直线与直线相交于点 , 下列说法正确的是( )A、直线恒过定点 B、直线与圆恒相交 C、直线 , 的交点在定圆上 D、若为中点,则的最小值为
-
7、已知 , 及两直线: , : , 作直线垂直于 , , 且垂足分别为C、D,则 , 的最小值为
-
8、已知正三棱锥的高为 ,且各顶点都在同一球面上. 若该球的体积为 ,则三棱锥体积的最大值是( )A、 B、 C、 D、
-
9、已知定义:函数的导函数为 , 我们称函数的导函数为函数的二阶导函数,如果一个连续函数在区间I上的二阶导函数 , 则称为I上的凹函数;二阶导函数 , 则称为I上的凸函数.若是区间I上的凹函数,则对任意的 , 有不等式恒成立(当且仅当时等号成立).若是区间I上的凸函数,则对任意的 , 有不等式恒成立(当且仅当时等号成立).已知函数 , .(1)、试判断在为凹函数还是凸函数?(2)、设 , , , , 且 , 求的最大值;(3)、已知 , 且当 , 都有恒成立,求实数a的所有可能取值.
-
10、已知函数 .(1)、当时,求函数的最小值;(2)、设方程的所有根之和为T,且 , 求整数n的值;(3)、若关于x的不等式恒成立,求实数a的取值范围.
-
11、如图所示的几何体中,四边形为矩形,平面 , , , , 点为棱的中点.
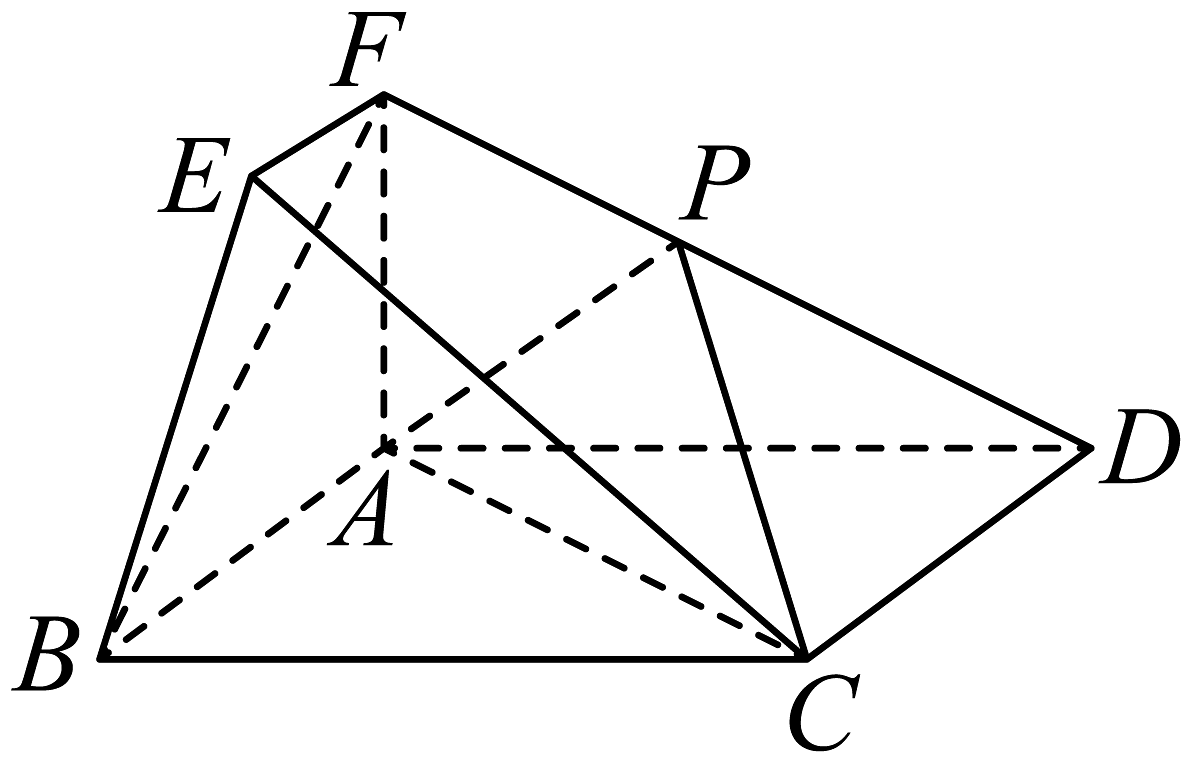 (1)、求证:平面;(2)、求平面与平面的夹角的余弦值;(3)、求点到平面的距离.
(1)、求证:平面;(2)、求平面与平面的夹角的余弦值;(3)、求点到平面的距离. -
12、在中,角A, , 所对的边分别为 , , , 且满足 , 的外接圆的半径为.(1)、求角的值;(2)、如果 , 求的面积;(3)、求内切圆半径的最大值.
-
13、已知函数 , 若对任意 , 有 , 则正整数的最小值为 .
(参考值: , )
-
14、已知正四面体中, , 、 , …,在线段上,且 , 过点(、、…、)作平行于直线、的平面,截面面积为 , 则所有截面积之和为.

-
15、如图,在正方体中,为线段的中点,为线段上的动点(不包括端点),则( )
 A、存在点 , 使得 B、存在点 , 使得平面 C、对于任意点Q,均不成立 D、三棱锥的体积是定值
A、存在点 , 使得 B、存在点 , 使得平面 C、对于任意点Q,均不成立 D、三棱锥的体积是定值 -
16、无穷等比数列的首项为公比为q,下列条件能使既有最大值,又有最小值的有( )A、 , B、 , C、 , D、 ,
-
17、在锐角中,已知 , 则 , 的大小关系为( )A、 B、 C、 D、无法确定
-
18、在1和15之间插入个数,使得这个数成等差数列.若这个数中第1个为 , 第个为 , 则的最小值是( )A、 B、2 C、 D、3
-
19、甲、乙、丙、丁四位同学在玩一个猜数字游戏.甲、乙、丙共同写出三个集合A,B,C,然后他们三人各用一句话来正确描述集合中“”表示的数字,并让丁同学猜出该数字.已知集合 , , . 甲、乙、丙三位同学描述如下.甲:此数为小于5的正整数;乙:是的必要不充分条件;丙:是的充分不必要条件.则“”表示的数字是( )A、1或2 B、2或3 C、3或4 D、1或3
-
20、正方体中,与的交点称为正方体的中心,若平面经过该正方体的中心 , 且顶点 , 到平面的距离相等,则符合条件的平面的个数为( )A、1个 B、2个 C、12个 D、无数个