相关试卷
-
1、已知 , , 则是的( )条件A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件
-
2、若复数满足 , 则( ).A、 B、 C、 D、
-
3、已知集合 , , 则( )A、 B、 C、 D、
-
4、下列命题中,不正确的命题是( )A、空间中任意两个向量一定共面 B、若 , 则存在唯一的实数 , 使得 C、对空间中任一点O和不共线的三点A,B,C,若 , 则P,A,B,C四点共面 D、若是空间的一个基底, , 则也是空间的一个基底
-
5、已知抛物线 , 直线交抛物线于两点,(1)、若线段中点的纵坐标为2,求直线的方程;(2)、若抛物线上存在两点关于直线轴对称,求的取值范围.(3)、若存在定点 , 使以为直径的圆上的任意点 , 都满足(为原点),求定点的坐标和的值.
-
6、设 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
7、已知动点到直线的距离比它到定点的距离多1(1)、求的方程;(2)、若过点的直线与相交于A,B两点,且 , 求直线的方程.
-
8、已知函数 , 且在上的最小值为0.(1)、求实数的取值范围;(2)、设函数在区间上的导函数为 , 若对任意实数恒成立,则称函数在区间上具有性质.
(i)求证:函数在上具有性质;
(ii)记 , 其中 , 求证:.
-
9、如图,广东省某机器人比赛设计了一个矩形场地ABCD(含边界和内部,A为坐标原点),AD长10米,在AB边上距离A点4米的F处放一只电子狗,在距A点2米的E处放一个机器人,机器人行走速度为v,电子狗行走速度为2v,若电子狗和机器人在场地内沿直线方向同时到达场地内某点M,那么电子狗将被机器人捕获,点M叫“成功点”.
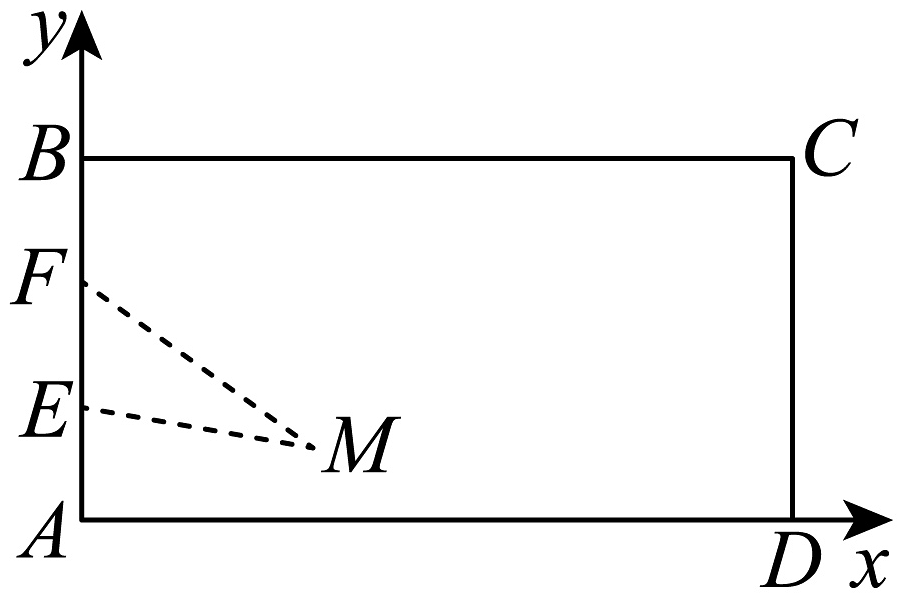 (1)、求在这个矩形场地内“成功点”M的轨迹方程;(2)、若P为矩形场地AD边上的一点,电子狗在线段FP上总能逃脱,求|AP|的取值范围.
(1)、求在这个矩形场地内“成功点”M的轨迹方程;(2)、若P为矩形场地AD边上的一点,电子狗在线段FP上总能逃脱,求|AP|的取值范围. -
10、已知直三棱柱中, , 分别为和的中点,为棱上的动点,.
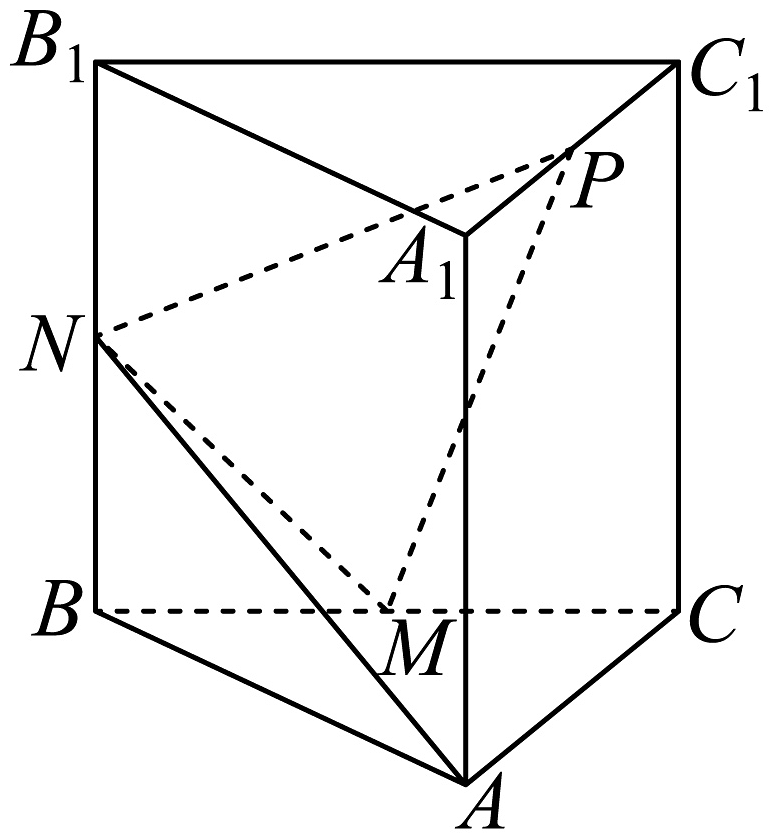 (1)、证明:平面平面;(2)、设 , 是否存在实数 , 使得平面与平面所成的角的余弦值为?
(1)、证明:平面平面;(2)、设 , 是否存在实数 , 使得平面与平面所成的角的余弦值为? -
11、已知数列中 , ,(1)、证明数列 是等比数列;(2)、若数列 的通项公式为 , 求数列 的前n项和.
-
12、已知的内角、、的对边分别为、、 , 且 .(1)、求;(2)、若 , 则面积为 , 求、的值.
-
13、若存在实数m,使得对于任意的 , 不等式恒成立,则取得最大值时, .
-
14、已知的外心为 , 内角的对边分别为 , 且.若 , 则.
-
15、已知函数 , 若 , , 且 , 则的最小值是 .
-
16、已知函数及其导函数的定义域均为 , 若是偶函数,且 , 令 , 则下列说法正确的是( )A、函数是奇函数 B、 C、函数的图象关于点对称 D、
-
17、已知数列的前项和为 , 则下列结论正确的是( )A、若是等差数列,且 , 则 B、若是等比数列,且 , 则 C、若 , 则是等差数列 D、若是公比大于1的等比数列,则
-
18、已知函数 , , 则( )A、与的值域相同 B、与的最小正周期相同 C、曲线与有相同的对称轴 D、曲线与有相同的对称中心
-
19、已知函数是定义在上的奇函数,当时, , 则下列说法正确的是( )A、函数有两个零点 B、当时, C、的解集是 D、都有
-
20、已知数列的前项和为 , 其中 , 且 , 则( )A、 B、 C、 D、