相关试卷
-
1、在正方体中,取为基,若点为平面的中心,且 , 则 .
-
2、已知向量 , , , 则( )A、 B、 C、 D、
-
3、已知直线l: , 则下列选项中正确的有( )A、直线l在y轴上的截距是2 B、直线l的斜率为 C、直线l不经过第三象限 D、直线l的一个方向向量为
-
4、如图,在三棱锥中, , , 平面 , 为的中点,则直线与平面所成角的余弦值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、过点且斜率为1的直线方程是( )A、 B、 C、 D、
-
6、已知点 , 则直线的斜率是( )A、 B、 C、 D、
-
7、若函数在区间上的值域恰为 , 则称区间为的一个“倒域区间”.已知定义在上的奇函数 , 当时,.(1)、求的解析式;(2)、若关于的方程在上恰有两个不相等的根,求的取值范围;(3)、求函数在定义域内的所有“倒域区间”.
-
8、2023年初,某品牌手机公司上市了一款新型大众智能手机.通过市场分析,生产此款手机每年需投入固定成本800万元,每生产x(千部)手机,需另投入成本万元,且已知此款手机售价0.7万元,且全年内生产的手机当年能全部销售完.(1)、求年利润(万元)关于年产量x(千部)的表达式;(2)、2023年年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
-
9、已知集合 , .(1)、若成立的一个必要条件是 , 求实数的取值范围;(2)、若 , 求实数的取值范围.
-
10、求值.
(1)且;
(2)
-
11、已知函数的定义域为 , 满足 , 且当时, , 若对任意 , 都有 , 则的最大值是.
-
12、函数是定义在上的偶函数,且当时, , 那么.
-
13、函数的定义域为.
-
14、已知定义在上的函数同时满足以下三个条件:①;②;③在区间上单调递增,则下列关于的表述中,正确的是( )A、 B、恰有三个零点 C、在上单调递增 D、存在最大值和最小值
-
15、下列命题,其中正确的命题是( )A、函数的最大值为 B、若 , 则的值为 C、函数的减区间是 D、已知在上是增函数,若 , 则
-
16、下列函数中为奇函数的是( )A、 B、 C、 D、
-
17、已知函数且的图象恒过定点 , 且点在直线上,则的最小值是( )A、 B、 C、 D、
-
18、已知函数在上是单调的函数,则实数a的取值范围是( ).A、 B、 C、 D、
-
19、函数()的图象大致为A、
 B、
B、 C、
C、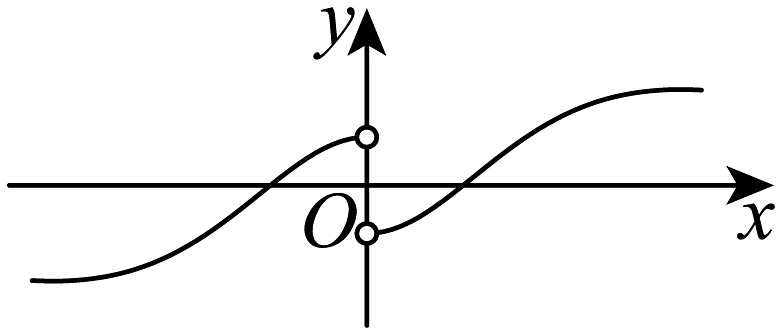 D、
D、
-
20、“是函数且)的图象经过第三象限”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件