相关试卷
-
1、对于集合A,B,定义集合且 , 已知集合 , , , 则( )A、 B、 C、 D、
-
2、函数f(x)=|x2﹣2x|,x1、x2、x3、x4满足:f(x1)=f(x2)=f(x3)=f(x4)=m,x1<x2<x3<x4且x2﹣x1=x3﹣x2=x4﹣x3 , 则m=( )
 A、 B、 C、1 D、
A、 B、 C、1 D、 -
3、黎曼猜想是解析数论里的一个重要猜想,它被很多数学家视为是最重要的数学猜想之一.它与函数(为常数)密切相关,请解决下列问题:(1)、当时,求在点处的切线方程;(2)、当时,证明有唯一极值点.
-
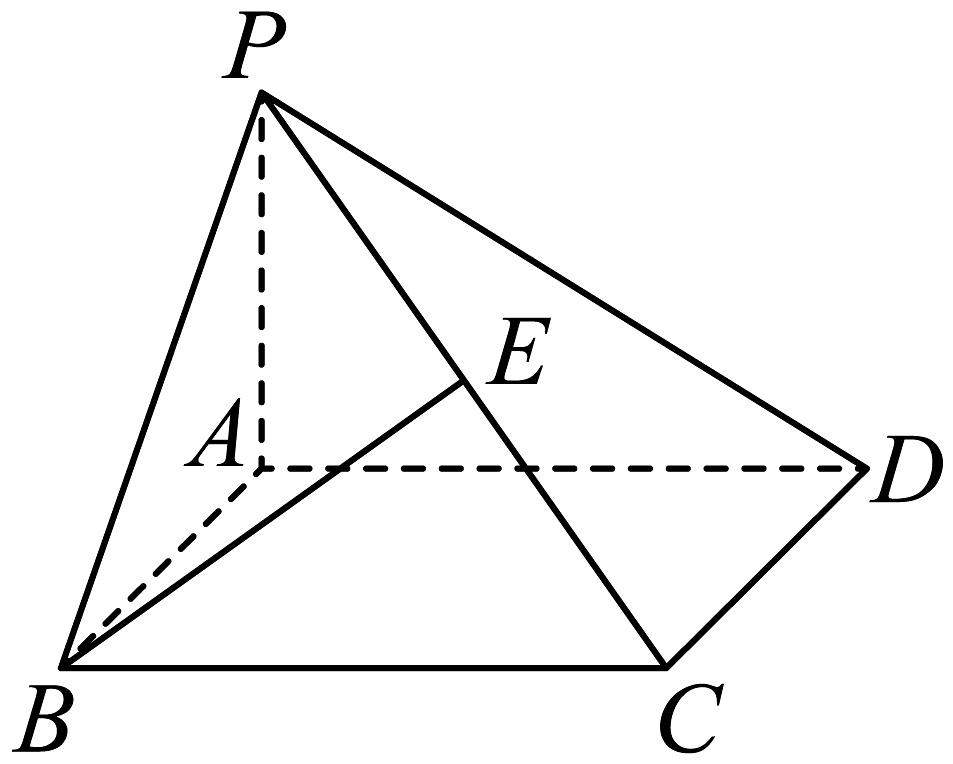
4、如图,在三棱锥中,底面为上一点,且平面平面 , 三棱锥的体积为.
 (1)、求证:为的中点;(2)、求直线与平面所成角的正弦值.
(1)、求证:为的中点;(2)、求直线与平面所成角的正弦值. -
5、一款便携式行李箱的密码是由数字1,2,3组成的一个五位数,这三个数字的每个数字在密码中至少出现一次,且它们出现的概率相等.(1)、求该款行李箱密码的不同种数;(2)、记X表示该款行李箱密码中数字1出现的次数,求X的分布列和数学期望.
-
6、在△中,角的对边分别为 , 已知(1)、求 ;(2)、若 分别为边 上的中点,为 的重心,求 的余弦值.
-
7、若 , 则 .
-
8、已知等差数列的首项 , 公差 , 求第10项的值为.
-
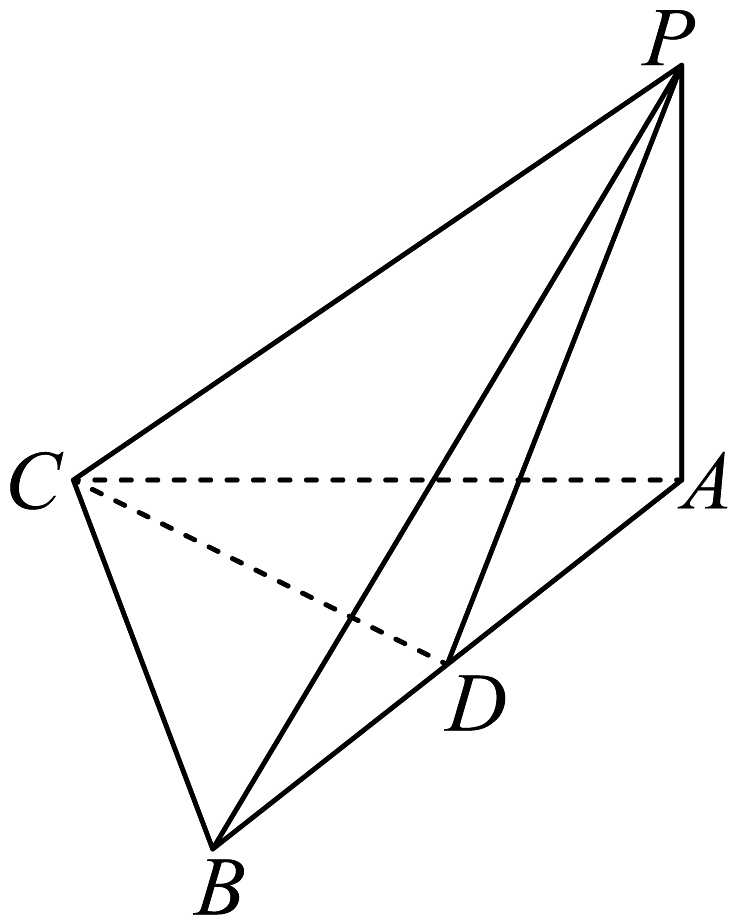
9、已知函数是定义在R上的奇函数,且 , 则 .
-
10、关于函数 , 下列说法正确的是( )A、当时,有两个零点 B、当时,在上单调递增 C、若关于的方程有两个不等实根,则 D、对任意两个正实数 , 且 , 若 , 则
-
11、对于定义在上的函数 , 若是奇函数,是偶函数,且在上单调递减,则( )A、 B、 C、 D、在上单调递减
-
12、已知等比数列 为递增数列,. 记 分别为数列 的前项和,若 , 则 ( )A、 B、 C、 D、
-
13、已知函数满足 , 则下列结论中正确的是( )A、 B、 C、 D、
-
14、蒙古包是我国蒙古族牧民居住的房子,适于牧业生产和游牧生活.如图所示的蒙古包由圆柱和圆锥组合而成,其中圆柱的高为 , 底面半径为是圆柱下底面的圆心.若圆锥的侧面与以为球心,半径为的球相切,则圆锥的侧面积为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
15、已知 , 是两个虚数,则“ , 均为纯虚数”是“为实数”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
16、已知集合 , 则( )A、 B、 C、 D、
-
17、已知直线 , 直线.(1)、若 , 求实数的值;(2)、若 , 求实数的值.
-
18、如图,在直四棱柱中, , , , 分别为棱 , , 的中点,建立如图所示的空间直角坐标系.
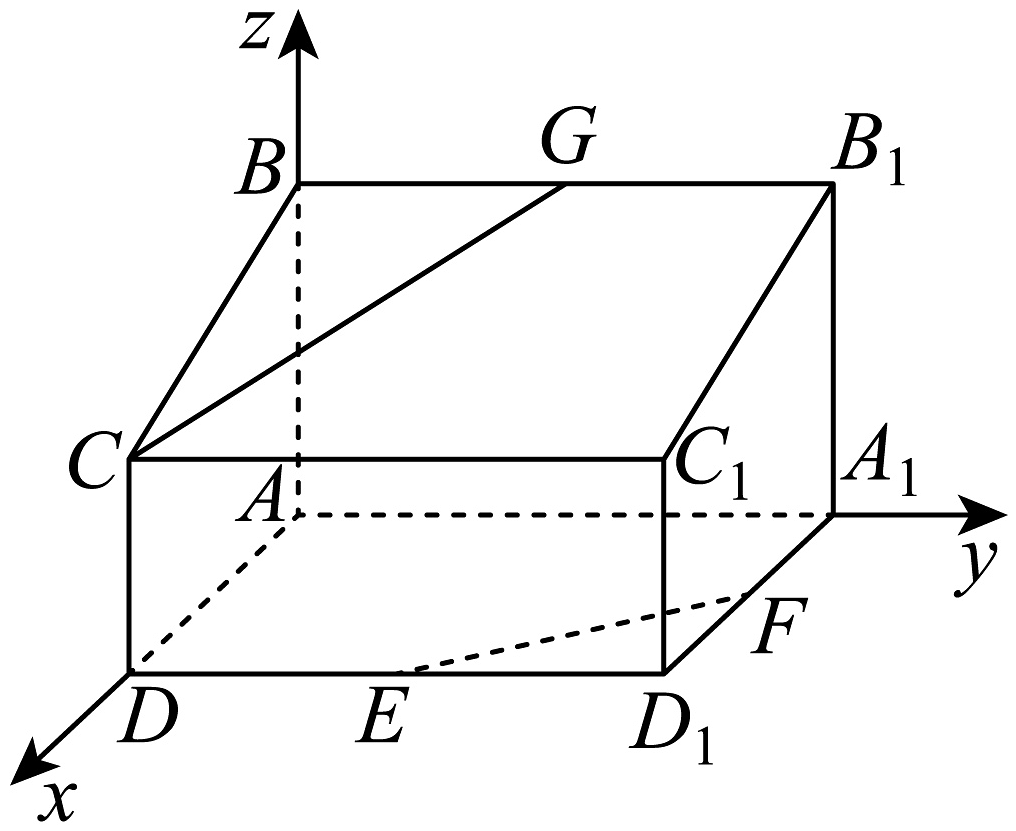 (1)、求的坐标;(2)、求的值
(1)、求的坐标;(2)、求的值 -
19、直线过点 , 则直线与轴正半轴、轴正半轴围成三角形面积的最小值为 .
-
20、如图,在四棱锥中,底面为矩形,底面 , , , 为的中点,则异面直线与所成角的余弦值为.