相关试卷
-
1、关于空间向量,以下说法不正确的是( )A、若两个不同平面α,β的法向量分别是 , 且 , 则 B、若直线l的方向向量为 , 平面α的法向量为 , 则直线l//α C、若对空间中任意一点O,有 , 则P,A,B,C四点共面 D、两个非零向量与任何一个向量都不能构成空间的一个基底,则这两个向量共线
-
2、在空间直角坐标系下,点关于平面的对称点的坐标为( )A、 B、 C、 D、
-
3、已知直线 , 下列结论正确的是( )A、直线的倾斜角为 B、直线的法向量为 C、直线的方向向量为 D、直线的斜率为
-
4、已知且 , 则下列不等式恒成立的是( )A、的最小值为2 B、的最小值为 C、ab的最大值为 1 D、的最大值为2
-
5、某公司携高端智能产品亮相展会,宣布将大举进军贵阳市场.该产品年固定研发成本为50万,每台产品生产成本为60元,展现了公司对技术创新的坚定投入与市场拓展的雄心壮志.贵阳市场将成为其展示智能科技魅力、引领生活新风尚的重要舞台.设该公司一年内生产该产品x万台且全部售完,每万台的销售收入为万元,.(1)、求年利润s(万元)关于年产量x(万台)的函数解析式;(利润销售收入成本)(2)、当年产量为多少万台时,该公司获得的利润最大?并求出最大利润.
-
6、设正实数x,y满足 , 则下列选项正确的有( )A、的最小值是 B、的最小值是4 C、的最小值为 D、的最大值为2
-
7、如图中的图象所表示的函数的解析式为( )
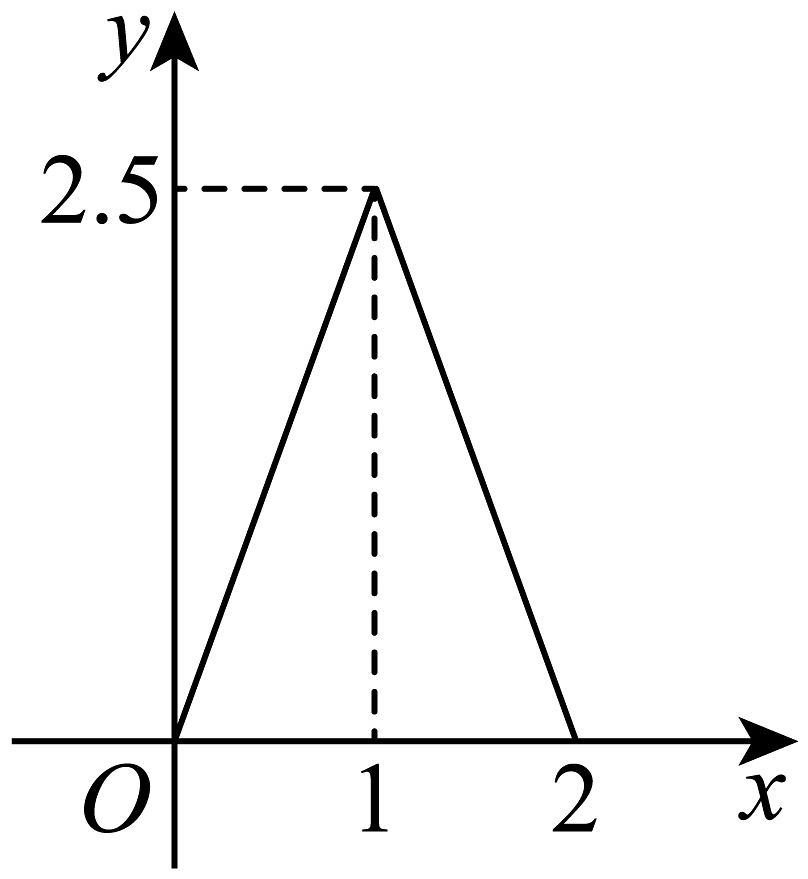 A、 B、 C、 D、
A、 B、 C、 D、 -
8、如图所示,平行六面体中, .
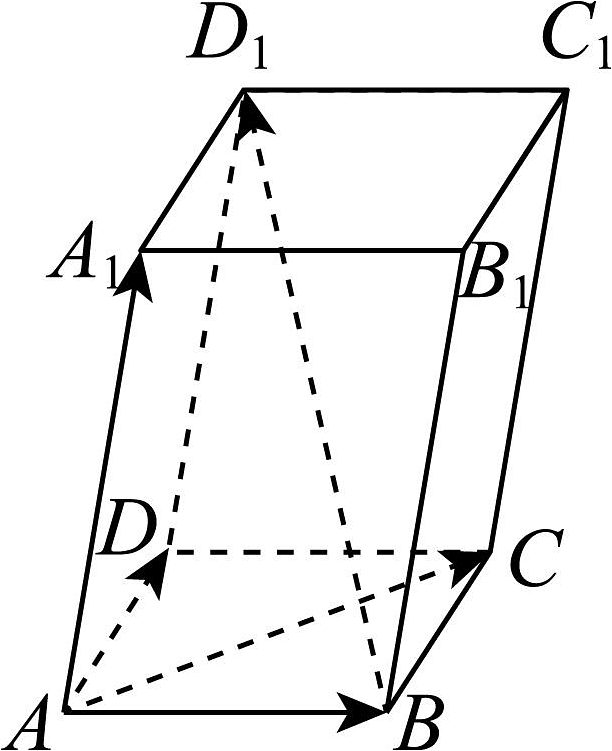 (1)、用向量表示向量 , 并求;(2)、求 .
(1)、用向量表示向量 , 并求;(2)、求 . -
9、如图,在三棱锥中,设 , 若 , , 则( )
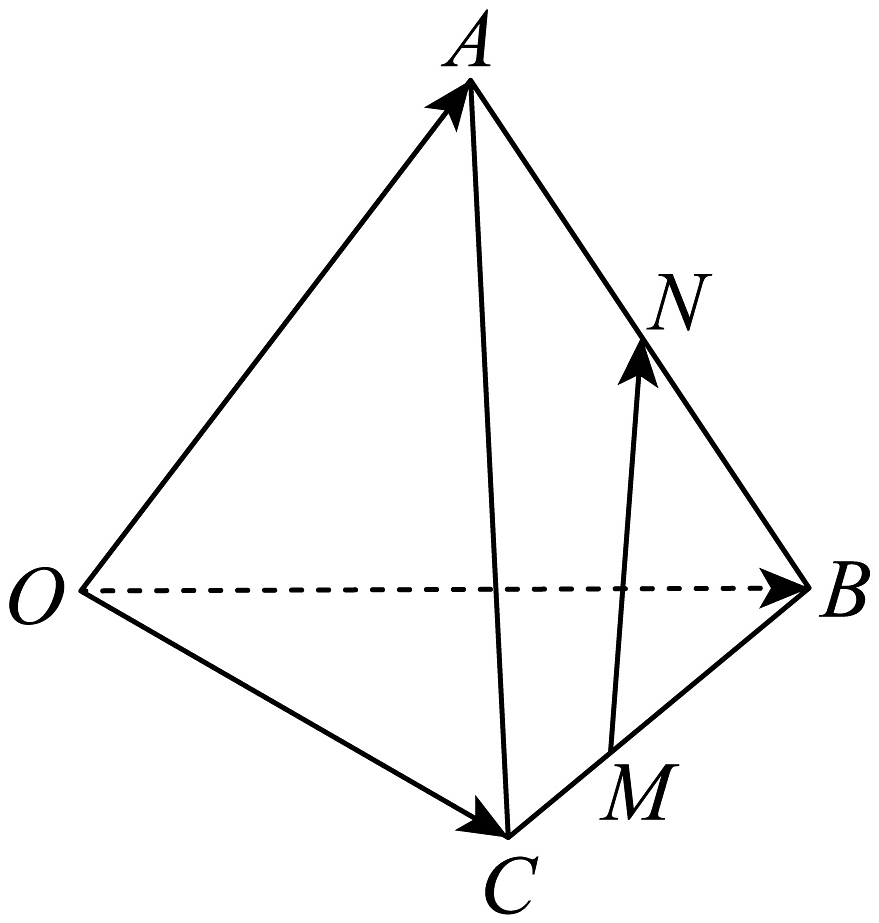 A、 B、 C、 D、
A、 B、 C、 D、 -
10、以下一些说法,其中正确的有( )A、一年按365天计算,两名学生的生日相同的概率是 B、买彩票中奖的概率是0.001,那么买1000张彩票一定能中奖 C、乒乓球比赛前,用抽签来决定谁先发球,抽签方法是从1~10共10个数中各抽取1个,再比较大小,这种抽签方法是公平的 D、昨天没有下雨,则说明关于气象局预报昨天“降水的概率为90%”是错误的
-
11、已知全集 , 集合或.(1)、求;(2)、求.
-
12、已知是二次函数,且满足 , .(1)、求函数的解析式;(2)、设函数 , 求在区间上的最小值的表达式;(3)、在(2)的条件下,对任意的 , 存在 , 使得不等式成立,求的取值范围.
-
13、函数且 过定点 , 则________
-
14、已知函数 , 则下列关于函数的结论错误的是( )A、 B、若 , 则的值是 C、的解集为 D、的值域为
-
15、已知正四棱柱中, , .
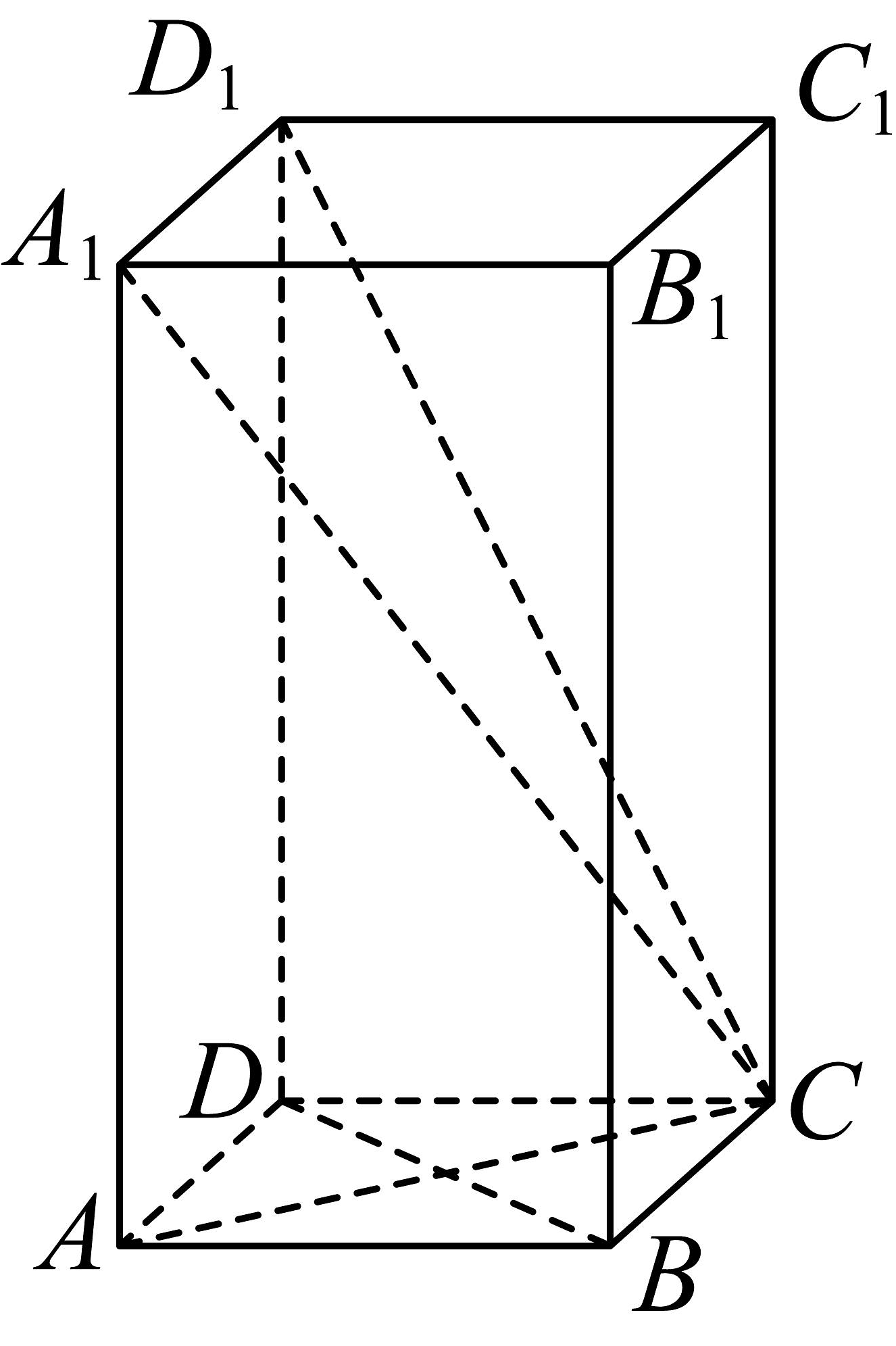 (1)、求异面直线与所成角的余弦值;(2)、求二面角的余弦值;(3)、在线段上是否存在点 , 使得平面平面 , 若存在,求出的值;若不存在,请说明理由.
(1)、求异面直线与所成角的余弦值;(2)、求二面角的余弦值;(3)、在线段上是否存在点 , 使得平面平面 , 若存在,求出的值;若不存在,请说明理由. -
16、如图,在四棱锥中,底面为矩形且 , 侧面底面 , 且侧面是正三角形,、分别是 , 的中点.
 (1)、求证:平面;(2)、求直线与平面所成角的余弦值.
(1)、求证:平面;(2)、求直线与平面所成角的余弦值. -
17、某中学为了组建一支业余足球队,在高一年级随机选取50名男生测量身高,发现被测男生的身高全部在到之间,将测量结果按如下方式分成六组:第1组 , 第2组 , …,第6组 , 如图是按上述分组得到的频率分布直方图,以频率近似概率.

(1)若学校要从中选1名男生担任足球队长,求被选取的男生恰好在第5组或第6组的概率;
(2)试估计该校高一年级全体男生身高的平均数(同一组中的数据用该组区间的中点值代表)与中位数;
(3)现在从第5与第6组男生中选取两名同学担任守门员,求选取的两人中最多有1名男生来自第5组的概率.
-
18、如图,在底面为菱形的平行六面体中,分别在棱上,且 , 且 .
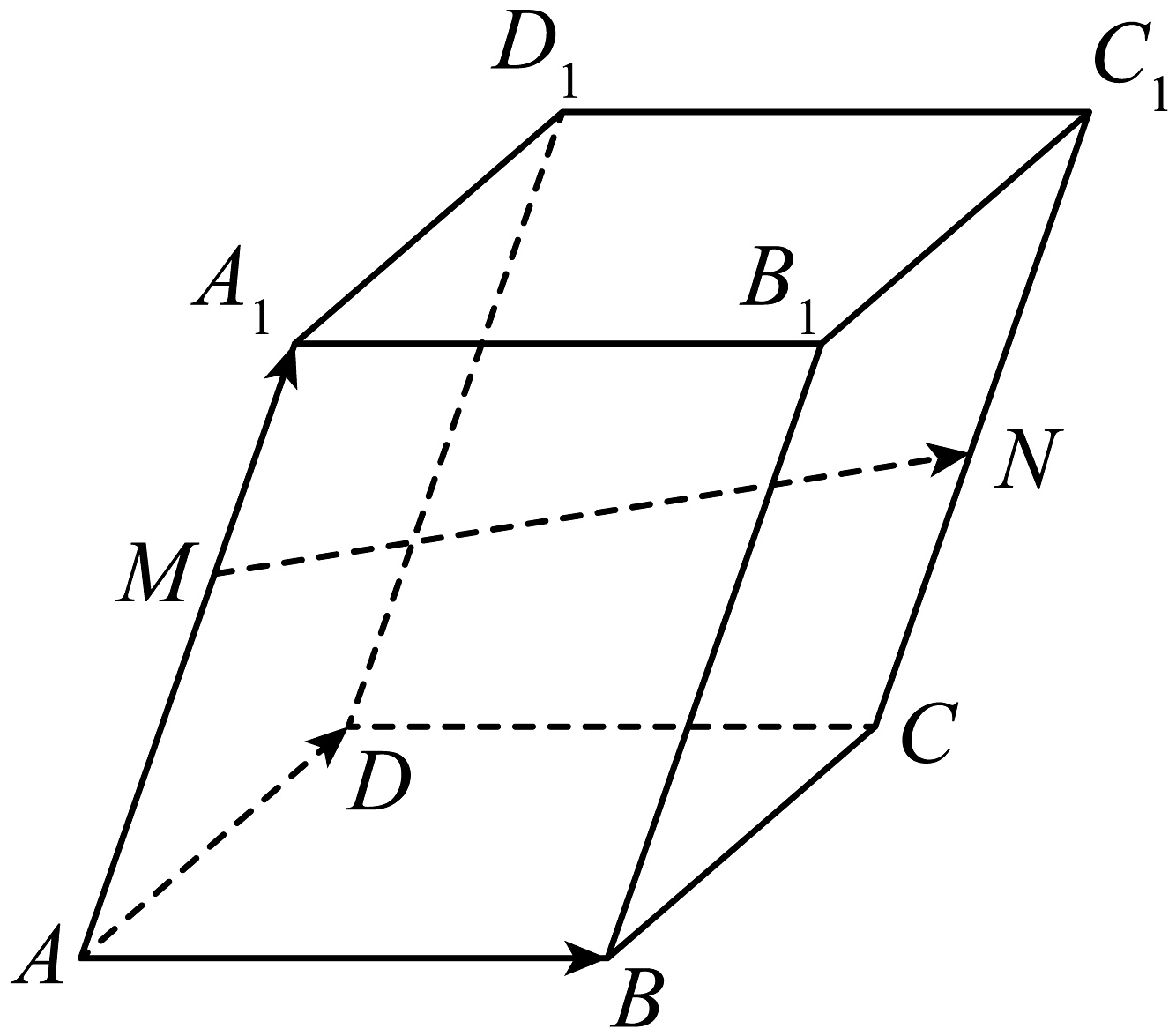 (1)、用向量表示向量;(2)、求证:共面;(3)、当为何值时, .
(1)、用向量表示向量;(2)、求证:共面;(3)、当为何值时, . -
19、某同学参加科普知识竞赛,需回答3个问题,竞赛规则规定:答对第一、二、三问题分别得100分、100分、200分,答错得零分,假设这名同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6,且各题答对与否相互之间没有影响.(1)、求这名同学得200分的概率;(2)、求这名同学至少得300分的概率.
-
20、如图,在直四棱柱中,底面是边长为1的菱形,高为2, , 则点到截面的距离为 .
