-
1、《瀑布》(图1)是最为人所知的作品之一,图中的瀑布会源源不断地落下,落下的水又逆流而上,荒唐至极,但又会让你百看不腻,画面下方还有一位饶有兴致的观察者,似乎他没发现什么不对劲.此时,他既是画外的观看者,也是埃舍尔自己.画面两座高塔各有一个几何体,左塔上方是著名的“三立方体合体”由三个正方体构成,右塔上的几何体是首次出现,后称“埃舍尔多面体”(图2)

埃舍尔多面体可以用两两垂直且中心重合的三个正方形构造,设边长均为2,定义正方形 , 的顶点为“框架点”,定义两正方形交线为“极轴”,其端点为“极点”,记为 , 将极点 , 分别与正方形的顶点连线,取其中点记为 , , , 如(图3).埃舍尔多面体可视部分是由12个四棱锥构成,这些四棱锥顶点均为“框架点”,底面四边形由两个“极点”与两个“中点”构成,为了便于理解,图4我们构造了其中两个四棱锥与
 (1)、求异面直线与成角余弦值;(2)、求平面与平面的夹角正弦值;(3)、求埃舍尔体的表面积与体积(直接写出答案).
(1)、求异面直线与成角余弦值;(2)、求平面与平面的夹角正弦值;(3)、求埃舍尔体的表面积与体积(直接写出答案). -
2、从出游方式看,春节期间是家庭旅游好时机.某地区消费者协会调查了部分2024年春节以家庭为单位出游支出情况,统计得到家庭旅游总支出(单位:百元)频率分布直方图,如图所示.(同一组中的数据用该组区间的中点值为代表)
 (1)、求的值;(2)、估计家庭消费总支出的第75百分位数.(3)、从和两组中用分层抽样的方法共抽取了6人,再从这6人中随机抽取2人,求所抽取的2人来自同一组的概率.
(1)、求的值;(2)、估计家庭消费总支出的第75百分位数.(3)、从和两组中用分层抽样的方法共抽取了6人,再从这6人中随机抽取2人,求所抽取的2人来自同一组的概率. -
3、对于任意实数 , 表示不超过的最大整数,如 , , 定义在上的函数 , 若 , , 则中所有元素的和为 .
-
4、甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若末命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为0.6,乙每次投篮的命中率均为0.8.由抽签确定第1次投篮的人选,第1次投篮的人是甲、乙的概率各为0.5.(1)、求第2次投篮的人是乙的概率;(2)、求第次投篮的人是甲的概率;(3)、已知:若随机变量服从两点分布,且 , 则 . 记前次(即从第1次到第次投篮)中甲投篮的次数为 , 求 .
-
5、已知空间向量 , , 且 , 则的值为( )A、 B、 C、 D、
-
6、判断下列各组直线是否平行,并说明理由.(1)、经过点 , 经过点;(2)、的斜率为 , 经过点.
-
7、如图,正方体的棱长为2,则下列说法正确的是( )
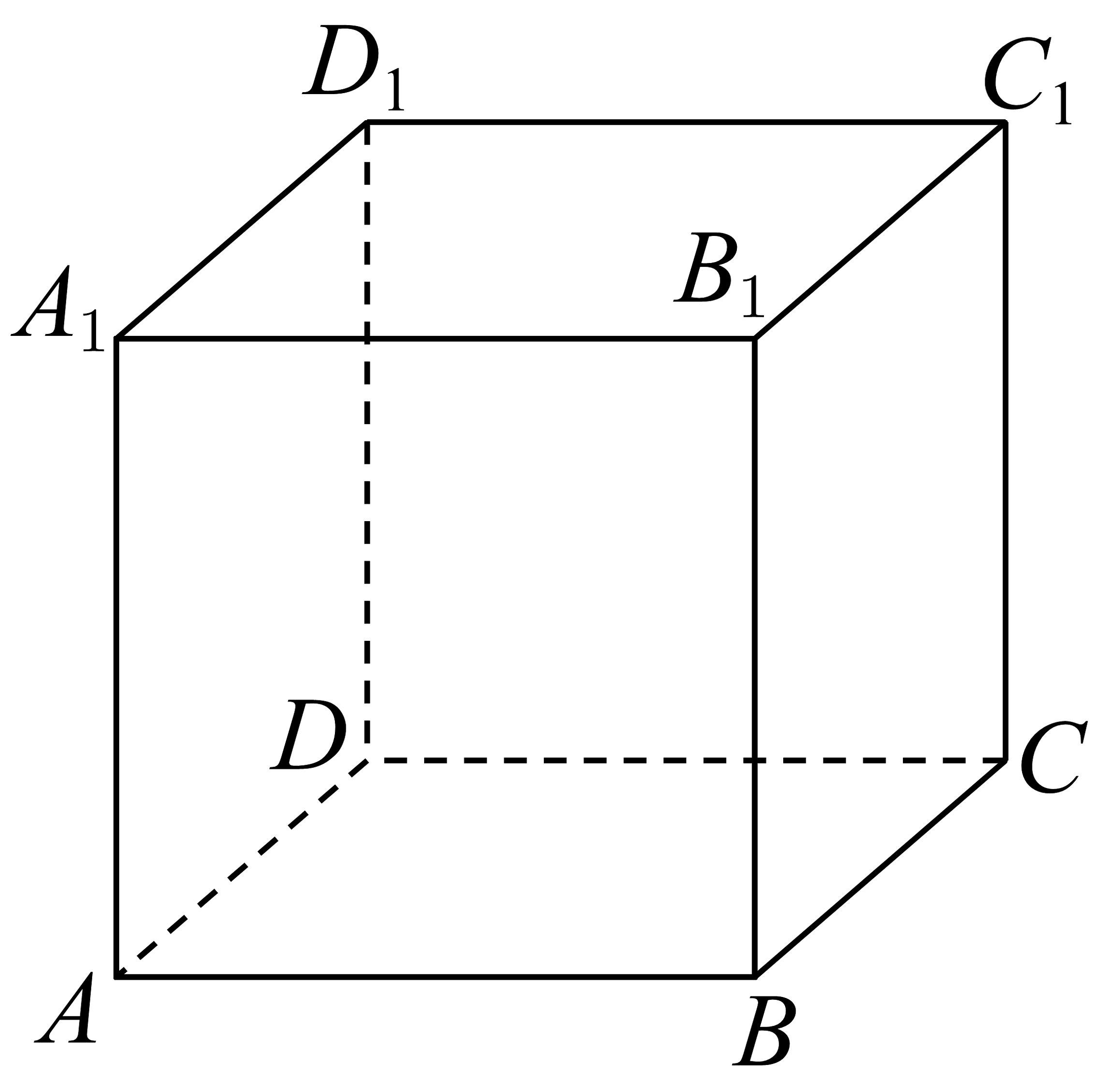 A、直线和所成的角为 B、四面体的体积是 C、点到平面的距离为 D、平面与平面夹角的正弦值为
A、直线和所成的角为 B、四面体的体积是 C、点到平面的距离为 D、平面与平面夹角的正弦值为 -
8、已知非零向量 , , 则“”是“向量”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
9、已知矩形的长为2,宽为1.(如图所示)
 (1)、若E为DC的中点,将矩形沿BE折起,使得平面平面 , 分别求到AB和AD的距离.(2)、在矩形ABCD中,点M是AD的中点、点N是AB的三等分点(靠近A点).沿折痕MN将翻折成 , 使平面平面.又点G,H分别在线段NB,CD上,若沿折痕GH将四边形向上翻折,使C与重合,求线段NG的长.
(1)、若E为DC的中点,将矩形沿BE折起,使得平面平面 , 分别求到AB和AD的距离.(2)、在矩形ABCD中,点M是AD的中点、点N是AB的三等分点(靠近A点).沿折痕MN将翻折成 , 使平面平面.又点G,H分别在线段NB,CD上,若沿折痕GH将四边形向上翻折,使C与重合,求线段NG的长. -
10、已知 , 则等于( )A、 B、 C、 D、
-
11、如图①所示,矩形中, , , 点M是边CD的中点,将沿AM翻折到 , 连接PB,PC,得到图②的四棱锥 , N为PB中点.
 (1)、求证:平面;(2)、若平面平面 , 求直线BC与平面所成角的大小;(3)、设的大小为θ,若 , 求平面和平面夹角余弦值的最小值.
(1)、求证:平面;(2)、若平面平面 , 求直线BC与平面所成角的大小;(3)、设的大小为θ,若 , 求平面和平面夹角余弦值的最小值. -
12、若函数满足:对任意正数 , 都有 , 则称函数为“H函数”.(1)、试判断函数与是否为“H函数”,并说明理由;(2)、若函数是“H函数”,求实数a的取值范围;(3)、若函数为“H函数”, , 对任意正数s、t,都有 , , 证明:对任意 , 都有 .
-
13、象棋是中国棋文化之一,也是中华民族的文化瑰宝,源远流长,雅俗共赏.某地举办象棋比赛,规定:每一局比赛中胜方得1分,负方得0分,没有平局.(1)、若甲、乙两名选手进行象棋比赛冠亚军的激烈角逐,每局比赛甲获胜的概率是 , 乙获胜的概率是 , 先得3分者夺冠,比赛结束.
(i)求比赛结束时,恰好进行了3局的概率;
(ii)若前两局甲、乙各胜一局,记表示到比赛结束还需要进行的局数,求的分布列及数学期望;
(2)、统计发现,本赛季参赛选手总得分近似地服从正态分布.若 , 则参赛选手可获得“参赛纪念证书”;若 , 则参赛选手可获得“优秀参赛选手证书”.若共有200名选手参加本次比赛,试估计获得“参赛纪念证书”的选手人数.(结果保留整数)附:若 , 则 , .
-
14、已知数列满足: , .(1)、求数列的通项公式;(2)、对任意 . 将数列中落入区间内的项的个数记为 , 求数列的前m项和 .
-
15、已知函数.
(1)若函数在区间上单调递增,求的取值范围;
(2)设函数 , 若存在 , 使不等式成立,求实数的取值范围.
-
16、如图,四边形为平行四边形, , 若 , 则的值为 .

-
17、如图,点是棱长为2的正方体的表面上一个动点,是线段的中点,则( )
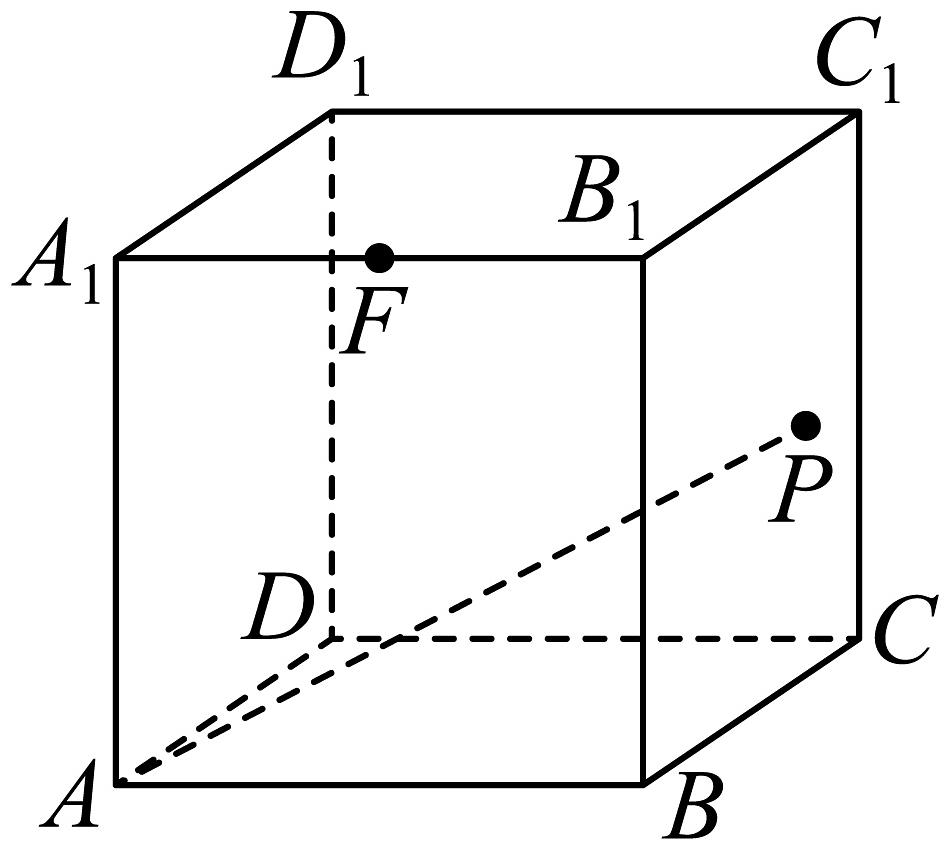 A、若点满足 , 则动点的轨迹长度为 B、三棱锥体积的最大值为 C、当直线与所成的角为时,点的轨迹长度为 D、当在底面上运动,且满足平面时,线段长度最大值为
A、若点满足 , 则动点的轨迹长度为 B、三棱锥体积的最大值为 C、当直线与所成的角为时,点的轨迹长度为 D、当在底面上运动,且满足平面时,线段长度最大值为 -
18、已知函数的定义域为R,且 , , 则( )A、 B、有最小值 C、 D、是奇函数
-
19、定义运算 . 在中,角A,B,C的对边分别为a,b,c,若a,b,c满足 , 则下列结论正确的是( )A、 B、 C、角B的最大值为 D、若 , 则为钝角三角形
-
20、已知函数 , 若当时,恒成立,则实数的取值范围是( )A、 B、 C、 D、