-
1、一般地,任何一个复数(a,)可以写成 , 其中r是复数的模,是以x轴非负半轴为始边,射线OZ为终边的角,称为复数的辅角.我们规定在范围内的辅角称为辅角主值,通常记作argz,如 , , .发现 , 就是说两个复数相乘,积的模等于各复数模的积,积的辅角等于各复数辅角的和.考虑如下操作:从写有实数0,1,的三张卡片中随机抽取两张,将卡片上的两个数依次作为一个复数的实部和虚部.设n为正整数,重复n次上述操作,可得到n个复数,将它们的乘积记为.(1)、写出一次操作后所有可能的复数;(2)、当 , 记的取值为X,求X的分布列;(3)、求为实数的概率.
-
2、在平面直角坐标系中,圆C的方程为: , 定点 , B是圆C上任意一点,线段BF的垂直平分线l和半径BC相交于点T.(1)、求点T的轨迹W的方程;(2)、已知点 , 过点F的一条直线,斜率不为0,交曲线W于P、Q两点,直线AP,AQ分别与直线交于M,N两点,求证:直线FM与直线FN的斜率之积为常数.
-
3、如图,三棱锥中, , 平面平面 , 平面平面.
 (1)、证明:平面;(2)、若为钝角,且二面角的大小为 , 求.
(1)、证明:平面;(2)、若为钝角,且二面角的大小为 , 求. -
4、已知函数 , 其中.(1)、若曲线在点处的切线垂直于直线 , 求a的值;(2)、讨论函数的单调性.
-
5、已知的内角A,B,C的对边分别为a,b,c,满足.(1)、求角A;(2)、若 , 的面积为 , 求的值.
-
6、一只盒子中装有4个形状大小相同的小球,小球上标有4个不同的数字.摸球人不知最大数字是多少,每次等可能地从中摸出一个球,不放回.摸球人决定放弃前面两次摸出的球,从第3次开始,如果摸出的球上标有的数字大于前面摸出的球上的数字,就把这个球保存下来,摸球结束,否则继续摸球.问摸球人最后保存下来是数字最大的球的概率是.
-
7、已知展开式的二项式系数之和为64,则展开式中项的系数为.(用数字作答)
-
8、如图,是边长为2的正方形, , , , 都垂直于底面 , 且 , 点在线段上,平面交线段于点 , 则( )
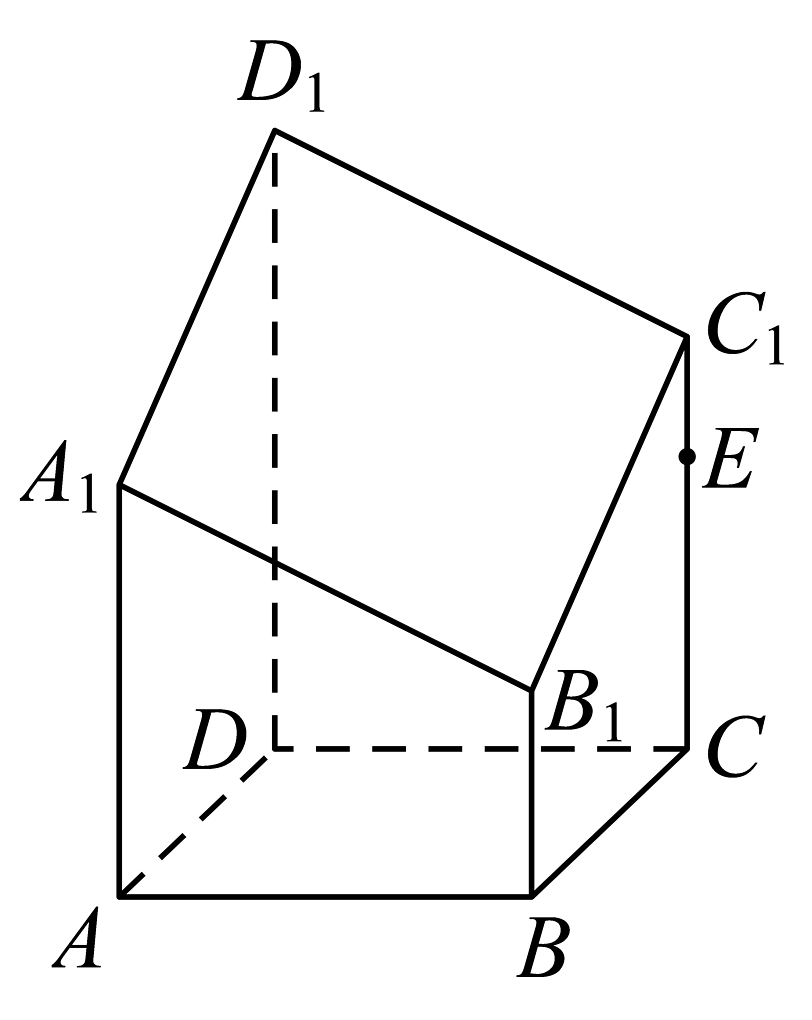 A、 , , , 四点不共面 B、该几何体的体积为8 C、过四点 , , , 四点的外接球表面积为 D、截面四边形的周长的最小值为10
A、 , , , 四点不共面 B、该几何体的体积为8 C、过四点 , , , 四点的外接球表面积为 D、截面四边形的周长的最小值为10 -
9、已知数列的前n项和为 , 满足 , 且 , 则下列结论中正确的是( )A、为等比数列 B、为等比数列 C、 D、
-
10、下列说法正确的是( )A、若随机变量 , 则 B、残差平方和越大,模型的拟合效果越好 C、若随机变量 , 则当减小时,保持不变 D、一组数据的极差不小于该组数据的标准差
-
11、已知是定义在上且不恒为0的连续函数,若 , , 则( )A、 B、为奇函数 C、的周期为2 D、
-
12、某袋子中有大小相同的4个白球和2个红球,甲乙两人先后依次从袋中不放回取球,每次取1球,先取到红球者获胜,则甲获胜的概率( )A、 B、 C、 D、
-
13、已知圆锥的侧面展开图是一个面积为的半圆,则该圆锥的高为( )A、 B、 C、 D、
-
14、“直线与圆有公共点”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
15、已知函数 , 则关于的不等式的解集为( )A、 B、 C、 D、
-
16、下列四个函数中,以为其对称中心,且在区间上单调递增的是( )A、 B、 C、 D、
-
17、已知 , 是不共线的单位向量,若 , , 且 , 则( )A、 B、 C、 D、
-
18、已知全集 , , , 则图中阴影部分对应的集合为( )
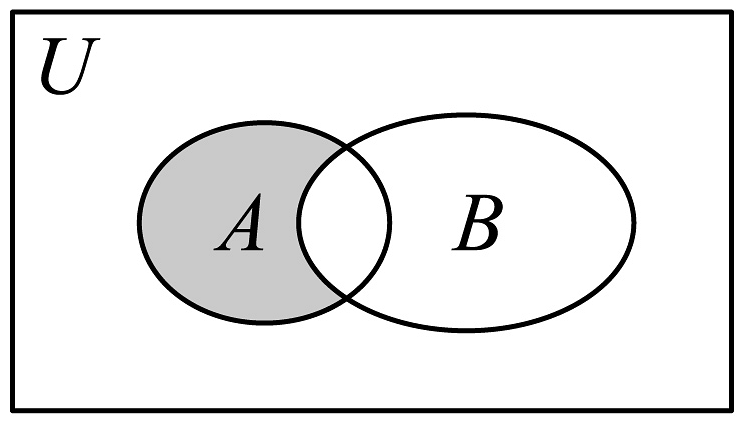 A、 B、 C、 D、
A、 B、 C、 D、 -
19、已知函数.(1)、求的图象的对称中心;(2)、当时,求的最值.
-
20、设函数 , .
(Ⅰ)已知 , 函数关于直线对称,求的值;
(Ⅱ)求函数在上的值域.