版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、定义：由椭圆的一个焦点和长轴的一个顶点（焦点与顶点在同一边）和短轴的一个顶点组成的三角形称为该椭圆的“焦顶三角形”，如果两个椭圆的”焦顶三角形”相似，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比，下列问题中（ $C_{1}$ 对应图1， $C_{2}$ 对应图2）.

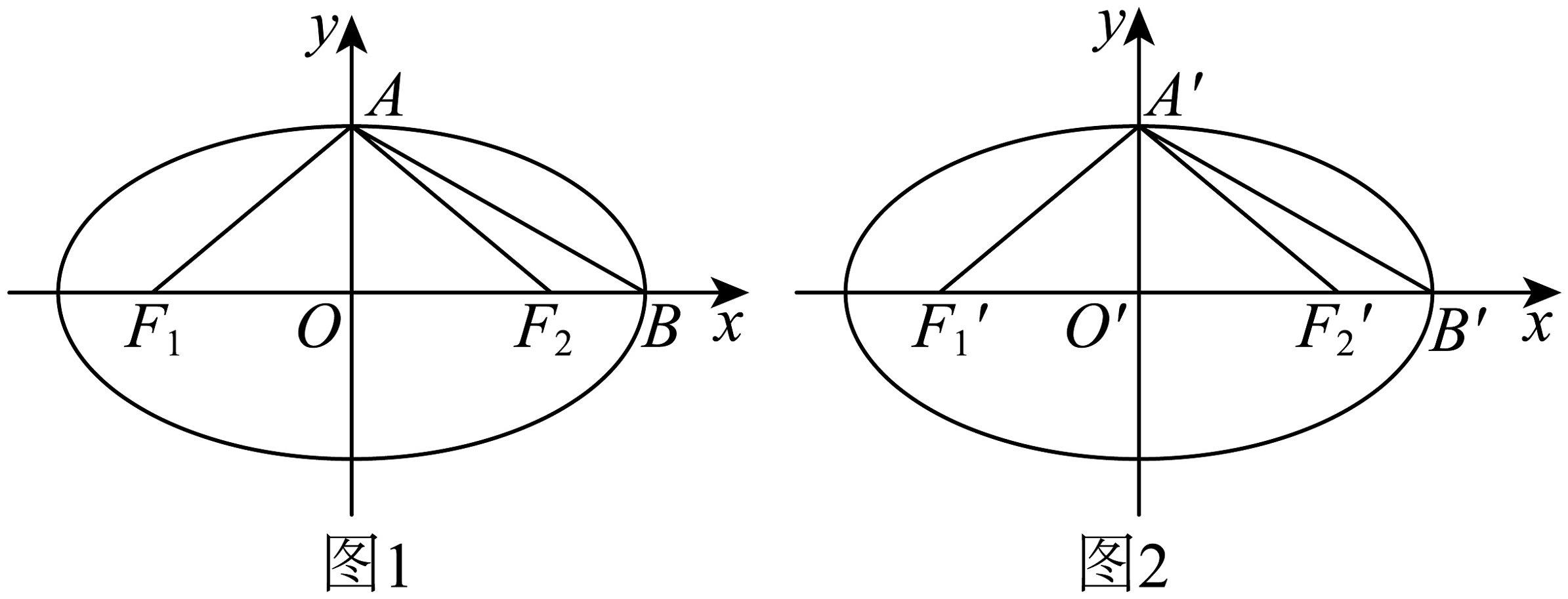(1)、判断椭圆 $C_{1} : \frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ 与椭圆 $C_{2} : \frac{x^{2}}{16} + \frac{y^{2}}{12} = 1$ 是否是“相似椭圆”? 若是，求出相似比；若不是，请说明理由；

(2)、证明：两个椭圆是“相似椭圆”的充要条件是离心率相等；

(3)、已知椭圆 $C_{1} : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 （ a > b > 0 ），$ 椭圆 $C_{2} : \frac{x^{2}}{a'^{2}} + \frac{y^{2}}{b'^{2}} = 1 （ a^{'} > b^{'} > 0 ）$ 的离心率为 $e^{'}$ ， $C_{1}$ 与 $C_{2}$ 是“相似椭圆”，且 $C_{1}$ 与 $C_{2}$ 的相似比为 $k : 1$ ，若 $△ A F_{2} B$ 的面积为 $S$ ，求 $△ A^{'} F_{1}^{'} F_{2}^{'}$ 的面积（用 $e^{'}$ ， $k$ ， $S$ 表示）.

查看解析
2、如图，在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $M$ ， $N$ 分别是棱 $A_{1} B_{1}$ ， $A_{1} D_{1}$ 的中点，点 $E$ 在 $B D$ 上，点 $F$ 在 $B_{1} C$ 上，且 $B E = C F$ ，点 $P$ 在线段 $C M$ 上运动，下列说法正确的有（）

A、当点 $E$ 是 $B D$ 中点时，直线 $E F / /$ 平面 $D C C_{1} D_{1}$ ； B、直线 $B_{1} D_{1}$ 到平面 $C M N$ 的距离是 $\frac{\sqrt{2}}{2}$ ； C、存在点 $P$ ，使得 $∠ B_{1} P D_{1} = 90 °$ ； D、 $△ P D D_{1}$ 面积的最小值是 $\frac{5 \sqrt{5}}{6}$

查看解析
3、连接抛物线上任意四点组成的四边形可能是（）

A、平行四边形 B、梯形 C、有三条边相等的四边形 D、有一组对角相等的四边形

查看解析
4、已知空间中三点 $A (0, 1, 0)$ ， $B (2, 2, 0)$ ， $C (- 1, 3, 1)$ ，则（）

A、 $\overset{⃑}{A B}$ 与 $\overset{⃑}{A C}$ 是共线向量 B、与向量 $\overset{⃑}{A B}$ 方向相同的单位向量坐标是 $(\frac{2 \sqrt{5}}{5}, \frac{\sqrt{5}}{5}, 0)$ C、 $\overset{⃑}{A B}$ 与 $\overset{⃑}{B C}$ 夹角的余弦值是 $\frac{\sqrt{55}}{11}$ D、 $\overset{⃑}{B C}$ 在 $\overset{⃑}{A B}$ 上的投影向量的模为 $\sqrt{5}$

查看解析
5、已知向量 $\vec{a} = (1, 1, 0), \vec{b} = (0, 1, 1), \vec{c} = (1, 2, 1)$ ，则下列结论正确的是（）

A、向量 $\vec{a}$ 与向量 $\vec{b}$ 的夹角为 $\frac{π}{3}$ B、 $\vec{c} ⊥ (\vec{a} - \vec{b})$ C、向量 $\vec{a}$ 在向量 $\vec{b}$ 上的投影向量为 $(\frac{1}{2}, 0, \frac{1}{2})$ D、向量 $\vec{c}$ 与向量 $\vec{a}, \vec{b}$ 共面

查看解析
6、已知函数 $f (x) = \sqrt{3} \sin (ω x + φ)$ （ $ω > 0$ ， $- \frac{π}{2} \leq φ \leq \frac{π}{2}$ ）的图象关于直线 $x = \frac{π}{3}$ 对称，且图象上相邻两个最高点的距离为 $π$ .

(1)、求 $ω$ 和 $φ$ 的值；

(2)、当 $x \in [0, \frac{π}{2}]$ 时，求函数 $y = f (x)$ 的最大值和最小值；

(3)、设 $g (x) = f (c x) (c > 0)$ ，若 $g (x)$ 图象的任意一条对称轴与 $x$ 轴的交点的横坐标不属于区间 $(π, 2 π)$ ，求 $c$ 的取值范围.

查看解析
7、如图所示，下列频率分布直方图显示了三种不同的分布形态.图（1）形成对称形态，图（2）形成“右拖尾”形态，图（3）形成“左拖尾”形态，根据所给图作出以下判断，正确的是（）

A、图（1）的平均数=中位数=众数 B、图（2）的众数<中位数<平均数 C、图（2）的众数<平均数<中位数 D、图（3）的平均数<中位数<众数

查看解析
8、如图，在四棱锥 $S - A B C D$ 中，底面 $A B C D$ 是直角梯形，侧棱 $S A ⊥$ 底面 $A B C D$ ， $A B$ 垂直于 $A D$ 和 $B C$ ， $S A = A B = B C = 2$ ， $A D = 1$ ． $M$ 是棱 $S B$ 的中点．
（1）求证： $A M / /$ 面 $S C D$ ；
（2）求二面角 $S - C D - M$ 的正弦值；
（3）在线段 $D C$ 上是否存在一点 $N$ 使得 $M N$ 与平面 $S A B$ 所成角的正弦值为 $\frac{\sqrt{35}}{7}$ 若存在，请求出 $\frac{D N}{D C}$ 的值，若不存在，请说明理由.

查看解析
9、下列事件中， $A, B$ 是相互独立事件的是（）

A、一枚硬币掷两次， $A =$ “第一次为正面”， $B =$ “第二次为反面” B、袋中有2个白球，2个黑球，不放回地摸两球， $A =$ “第一次摸到白球”， $B =$ “第二次摸到白球” C、掷一枚骰子， $A =$ “出现点数为奇数”， $B =$ “出现点数为3或4” D、掷一枚骰子， $A =$ “出现点数为奇数”， $B =$ “出现点数为偶数”

查看解析
10、下面命题正确的是（）

A、“ $a > 1$ ”是“ $\frac{1}{a} < 1$ ”的充分不必要条件 B、命题“任意 $x < 1$ ，则 $x^{2} < 1$ ”的否定是“存在 $x < 1$ ，则 $x^{2} \geq 1$ ” $.$ C、设 $x ， y \in R$ ，则“ $x \geq 2$ 且 $y \geq 2$ ”是“ $x^{2} + y^{2} \geq 4$ ”的必要而不充分条件 D、设 $a ， b \in R$ ，则“ $a \neq 0$ ”是“ $a b \neq 0$ ”的必要不充分条件

查看解析
11、下列关系中，正确的有（）

A、 $\emptyset$ $\begin{matrix} \subset \\ \neq \end{matrix}$ $\{0\}$ B、 $\frac{1}{3} \in Q$ C、 $Q \subseteq Z$ D、 $\emptyset \in \{0\}$

查看解析
12、已知实数 $a, b$ 满足 $a < b$ ，则下列不等式一定成立的是（）

A、 $\frac{1}{a} > \frac{1}{b}$ B、 $a^{2} < b^{2}$ C、 $a c < b c$ D、 $a - c < b - c$

查看解析
13、已知命题 $p$ ： $\forall x \in R, x^{2} + x + 1 > 0$ ，那么 $\neg p$ 是（）

A、 $\exists x_{0} \in R, {x_{0}}^{2} + x_{0} + 1 > 0$ B、 $\forall x \in R, x^{2} + x + 1 \leq 0$ C、 $\exists x_{0} \in R, {x_{0}}^{2} + x_{0} + 1 \leq 0$ D、 $\forall x \in R, x^{2} + x + 1 < 0$

查看解析
14、下列四个图形中，不是函数图象的是（）

A、 B、 C、 D、

查看解析
15、设全集 $U = R$ ，集合 $M = {- 1, 0, 1, 2, 3}$ ， $N = {x \in R | x > 1}$ ，则下面Venn图中阴影部分表示的集合是（）

A、 $(- \infty, 1)$ B、 $(- \infty, 1]$ C、 ${- 1, 0}$ D、 ${- 1, 0, 1}$

查看解析
16、设函数 $f (x) = x \ln x - a (x^{2} - 1)$ ．

(1)、若曲线 $y = f (x)$ 在点 $(1, 0)$ 处的切线方程为 $x + y - 1 = 0$ ，求a的值；

(2)、当 $x > 1$ 时 $f (x) < 0$ 恒成立，求实数a的取值范围；

(3)、证明： $\sum_{k = 2}^{n} \frac{\ln k}{k - 1} < 2 \sqrt{n} - 2 (n \in N^{*})$ ．

查看解析
17、在平面直角坐标系 $x O y$ 中，已知 $△ A B C$ 的三个顶点 $A (m, n), B (2, 1), C (- 2, 3)$ .

(1)、求 $B C$ 边所在直线的方程；

(2)、若 $△ A B C$ 的面积等于7，且点 $A$ 的坐标满足 $2 m - 3 n + 6 = 0$ ，求点 $A$ 的坐标.

查看解析
18、已知圆 $O : x^{2} + y^{2} = 1$ 和圆 $O_{1} : {(x - 2)}^{2} + y^{2} = 1$ ，过动点 $P$ 分别作圆 $O$ ，圆 $O_{1}$ 的切线 $P A$ ， $P B$ （A， $B$ 为切点），且 $| P A |^{2} + | P B |^{2} = 18$ ，则 $| P A |$ 的最大值为.

查看解析
19、已知直线 $l_{1} : (a + 2) x + 3 y + 4 = 0$ ， $l_{2} : x + a y - 4 = 0$ ，则（）

A、当 $a = 0$ 时，直线 $l_{1}$ 的一个方向向量为 $(2, 3)$ B、若 $l_{1}$ 与 $l_{2}$ 相互平行，则 $a = - 3$ 或 $1$ C、若 $l_{1} ⊥ l_{2}$ ，则 $a = - \frac{1}{2}$ D、若 $l_{1}$ 不经过第二象限，则 $a \leq - 2$

查看解析
20、已知随机事件A，B，C中， $A$ 与 $B$ 相互独立， $B$ 与 $C$ 对立，且 $P (A) = 0.3$ ， $P (C) = 0.6$ ，则 $P (A \cup B) =$ （）

A、0.4 B、0.58 C、0.7 D、0.72

查看解析

上一页 881 882 883 884 885 下一页跳转