-
1、下列结论正确的是( )A、直线的方向向量 , 平面的法向量 , 则 B、两个不同的平面 , 的法向量分别是 , , 则 C、若直线的方向向量 , 平面的法向量 , 若 , 则实数 D、若 , , , 则点在平面内
-
2、已知椭圆的焦点为 , , 是椭圆上一点,且 , 若的内切圆的半径满足 , 则椭圆的离心率为( )A、 B、 C、 D、
-
3、已知 , , , 其中 , 则下列选项正确的是( )A、 B、 C、 D、
-
4、已知离心率为2的双曲线 , 过右焦点且垂直于轴的直线与双曲线交于、两点,设、到双曲线的同一条渐近线的距离分别为和 , 且 , 则双曲线的方程为( )A、 B、 C、 D、
-
5、已知正四棱柱中, , 则到平面的距离为( )A、4 B、2 C、 D、
-
6、空间内有三点 , , , 则点到的中点的距离为( )A、 B、 C、 D、
-
7、已知集合 , 则的非空真子集的个数为( )A、1 B、2 C、3 D、4
-
8、已知圆 , 直线与圆交于 , 两点,过 , 分别作直线的垂线,垂足分别为分别异于.(1)、求实数的取值范围;(2)、若 , 用含的式子表示四边形的面积;(3)、当时,若直线和直线交于点 , 证明点在某条定直线上运动,并求出该定直线的方程.
-
9、在中,顶点 , 点在直线上,点在轴上,则周长的最小值为.
-
10、已知圆的方程是 , 则圆心的坐标是( )A、 B、 C、 D、
-
11、设的三个角A,B,C的对边分别为a,b,c,且(1)、求B;(2)、若 , 求的面积.
-
12、《易经》是中华民族智慧的结晶,易有太极,太极生两仪,两仪生四象,四象生八卦,易经包含了深刻的哲理.如图所示是八卦模型图以及根据八卦图抽象得到的正八边形 , 其中为正八边形的中心,则.

-
13、若点在圆C:的外部,则m的取值可能为( )A、5 B、1 C、 D、
-
14、已知双曲线(a>0,b0)的离心率为2,则该双曲线的渐近线方程为 .
-
15、如图所示的多面体中,四边形ABCD是菱形且 , , 平面ABCD, , 点N为PC上的动点.
 (1)、求证:存在点N,使得.(2)、求二面角的正弦值.
(1)、求证:存在点N,使得.(2)、求二面角的正弦值. -
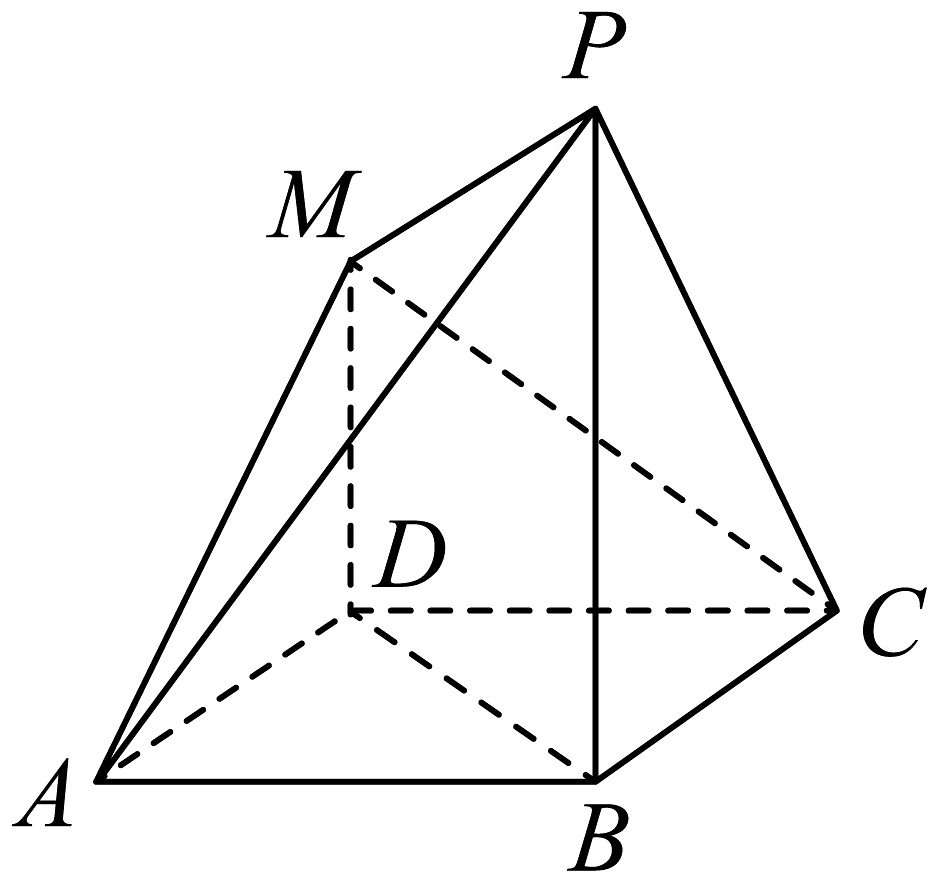
16、已知四棱锥中,底面是矩形, , , 是的中点.
 (1)、证明:;(2)、若 , , 点是上的动点,直线与平面所成角的正弦值为 , 求 .
(1)、证明:;(2)、若 , , 点是上的动点,直线与平面所成角的正弦值为 , 求 . -
17、给出下列命题,其中正确的命题是( )A、若 , 则是钝角 B、若 , 则可知 C、若为直线l的方向向量,则λ也是直线l的方向向量 D、在四面体中,若 , , 则
-
18、已知函数.
(1)若函数为奇函数,求a的值,并求此时函数的值域;
(2)若存在 , 使 , 求实数a的取值范围.
-
19、某摩天轮示意图如图.已知该摩天轮的半径为30米,轮上最低点与地面的距离为2米,沿逆时针方向匀速旋转﹐旋转一周所需时间为分钟.在圆周上均匀分布12个座舱,标号分别为1~12(可视为点).现4号座舱位于圆周最上端,从此时开始计时,旋转时间为t分钟.
 (1)、求1号座舱与地面的距离h与时间t的函数关系的解析式;(2)、在前24分钟内,求1号座舱与地面的距离为17米时t的值;(3)、记1号座舱与5号座舱高度之差的绝对值为H米,若在这段时间内,H恰有三次取得最大值,求的取值范围.
(1)、求1号座舱与地面的距离h与时间t的函数关系的解析式;(2)、在前24分钟内,求1号座舱与地面的距离为17米时t的值;(3)、记1号座舱与5号座舱高度之差的绝对值为H米,若在这段时间内,H恰有三次取得最大值,求的取值范围. -
20、已知函数(且)的图象过点 .(1)、求a的值及的定义域;(2)、求的单调区间;(3)、若 , 比较与的大小.