-
1、某中学新高一经过前期模拟选科摸底情况确定开设物化生,物化政,物化地及政史地四个模块供高一学生选择(物化生,物化政,物化地统称为物理类,政史地称为历史类),下图是该校高一名学生选择各个模块扇形统计图.已知该校学生选择物理类男女比例为 , 选择历史类男女比例为 .

男生
女生
合计
物理类
历史类
合计
1000
完成2×2列联表,并判断能否有99%把握认为“该校学生选择物理类是否与性别有关”?
附: .
0.05
0.01
0.001
k
3.841
6.635
10.828
-
2、在中,设角 , , 的对边分别为 , , .已知向量 , , 且.(1)、求角的大小;(2)、若 , , 求的面积.
-
3、已知函数在区间上没有零点,则实数的取值范围是 .
-
4、 .
-
5、设函数 , 则( )A、当时,是的极小值点 B、当时,有三个零点 C、当时,若在上有最大值,则m的取值范围为 D、若满足 , 则
-
6、若 , 则( )A、 B、 C、 D、
-
7、已知函数有4个不同的零点,则的取值可以为( )A、 B、 C、 D、0
-
8、若 , 恒成立,则实数的取值范围是( )A、 B、 C、 D、
-
9、已知且 , 则的最小值为( )A、12 B、 C、16 D、
-
10、函数的图像大致是( )A、
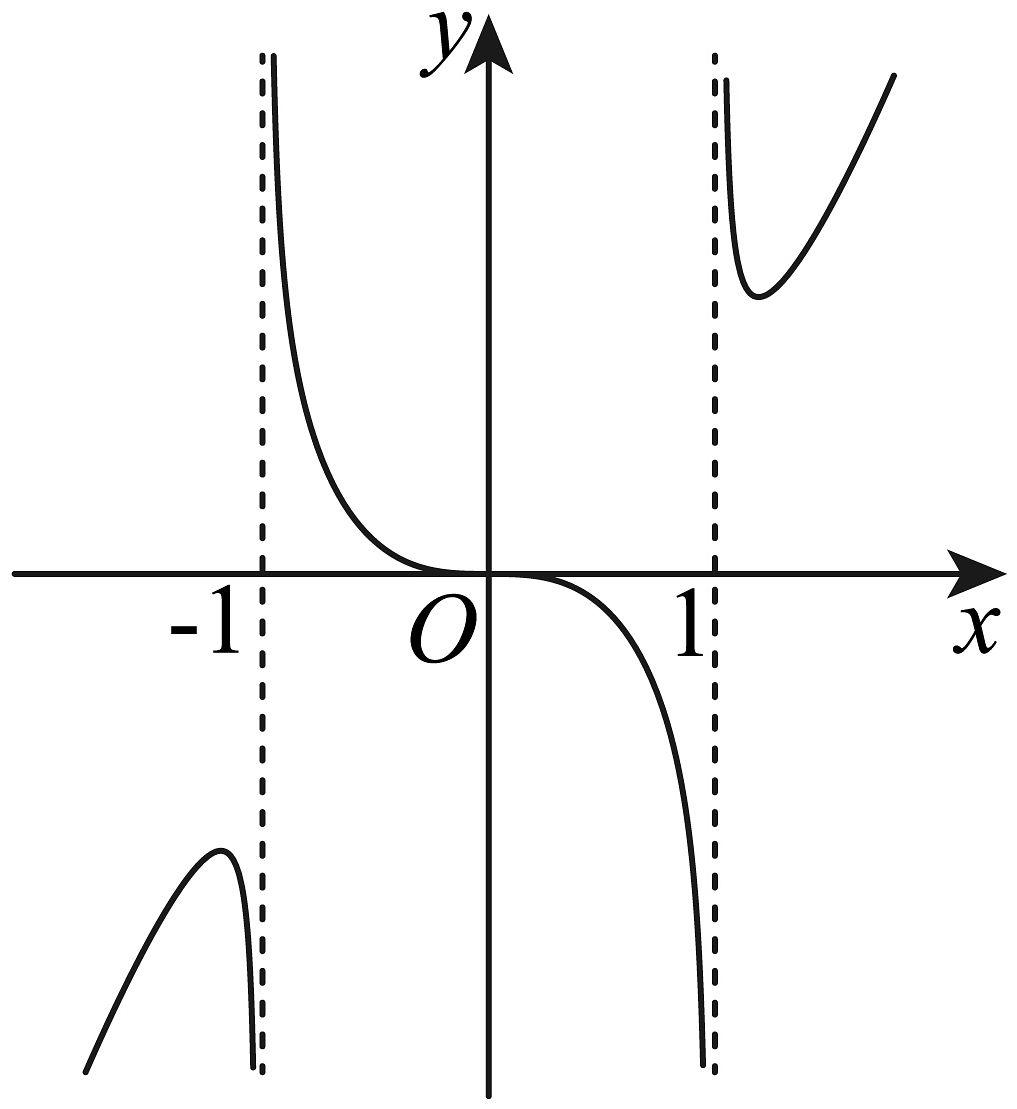 B、
B、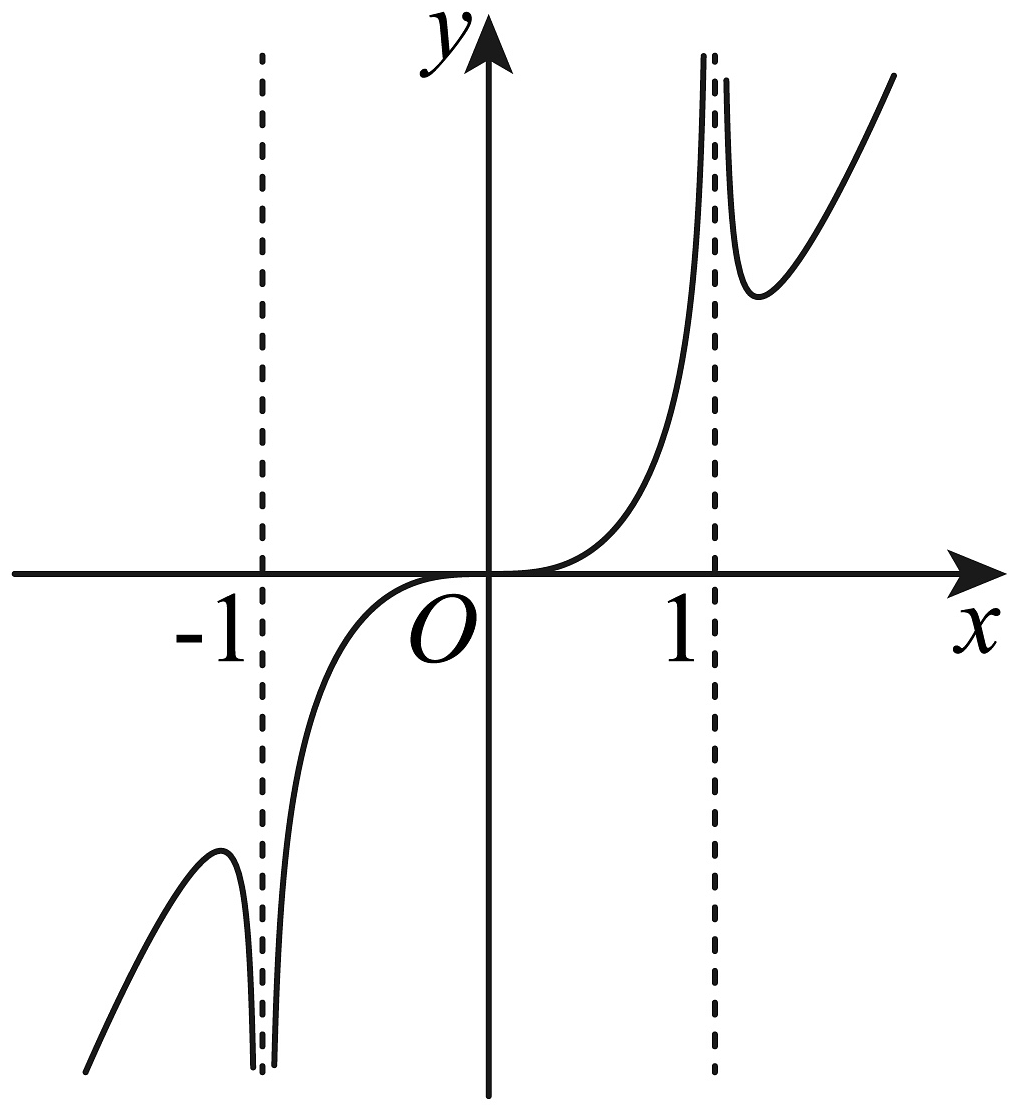 C、
C、 D、
D、
-
11、设 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
12、如图,在四棱锥中,底面 , , , , , 点E为棱PC的中点.证明:
 (1)、平面;(2)、平面平面 .
(1)、平面;(2)、平面平面 . -
13、函数的图象大致为( )A、
 B、
B、 C、
C、 D、
D、
-
14、拉格朗日中值定理是微积分学的基本定理之一,它与导数和函数的零点有关,其表达如下:若函数在区间连续,在区间上可导,则存在 , 使得 , 我们将称为函数在上的“中值点”.已知函数 , , .(1)、求在上的中值点的个数;(2)、若对于区间内任意两个不相等的实数 , , 都有成立,求实数t的取值范围.(3)、当且时,证明: .
-
15、已知椭圆C:()的离心率为 , 且过点 . 直线与椭圆C相切于点P(P在第一象限),直线与椭圆C相交于A,B两点,O为坐标原点.(1)、求椭圆C的方程;(2)、设直线OP的斜率为 , 求证:为定值;(3)、求△PAB面积的最大值.
-
16、已知各项均不为0的数列的前n项和为 , 且 , , , 数列的前n项和为 .(1)、求的通项公式;(2)、求;(3)、若对于任意 , 成立,求实数的取值范围.
-
17、在△ABC中,内角所对的边分别为 , 且 .(1)、证明:;(2)、若外接圆的面积为 , 且 , 求△ABC的面积.
-
18、已知 , .(1)、当时,求的图像在处的切线方程;(2)、若当时, , 求a的取值范围.
-
19、用表示不超过x的最大整数,例如 , , . 已知数列满足 , , 则.
-
20、在中, , , 则面积的最大值为.