-
1、已知定义在上的函数不恒等于 , 且对任意的 , 有 , 则( )A、 B、是偶函数 C、的图象关于点中心对称 D、是的一个周期
-
2、已知 , , 设 , 则关于的说法正确的是( )A、最大值为3,最小值为 B、最大值为 , 无最小值 C、单调递增区间为和 , 单调递减区间为和 D、单调递增区间为和 , 单调递减区间为和
-
3、已知函数的图象如图所示,图象与轴的交点为 , 与轴的交点为 , 最高点 , 且满足 . 若将的图象向左平移1个单位得到的图象对应的函数为 , 则( )
 A、 B、0 C、 D、
A、 B、0 C、 D、 -
4、下列不等式,正确的是( )A、 B、 C、 D、
-
5、设集合 , , 则( )A、 B、 C、 D、
-
6、已知直线 , 䒴 , , 则( )A、或 B、 C、或 D、
-
7、过点 , 倾斜角为的直线方程为( )A、 B、 C、 D、
-
8、直线族是指具有某种共同性质的直线的全体,例如表示过点的直线族(不包括直线轴),直线族的包络曲线定义为:直线族中的每一条直线都是该曲线上某点处的切线,且该曲线上的每一点处的切线都是该直线族中的某条直线.(1)、圆:是直线族的包络曲线,求 , 满足的关系式;(2)、若点不在直线族的任意一条直线上,求的取值范围及直线族的包络曲线的方程;(3)、在(1)(2)的条件下,过曲线上动点向圆做两条切线 , , 交曲线于点 , , 求面积的最小值.
-
9、在中,角对应的三边分别是 , , , 且.(1)、求角的值;(2)、若 , , 求的面积.
-
10、若 , 已知数列中,首项 , , , 则.
-
11、抛物线:的焦点为 , 为上一点且 , 为坐标原点,则.
-
12、如图,在直三棱柱中, , , 是线段的中点,是线段上的动点(含端点),则下列命题正确的是( )
 A、三棱锥的体积为定值 B、在直三棱柱内部能够放入一个表面积为的球 C、直线与所成角的正切值的最小值是 D、的最小值为
A、三棱锥的体积为定值 B、在直三棱柱内部能够放入一个表面积为的球 C、直线与所成角的正切值的最小值是 D、的最小值为 -
13、古代农耕常用水车作为灌溉引水的工具,是人类的一项古老的发明,也是人类改造自然的成果之一.如图是一个半径为的水车,以水车的中心为原点,过水车的中心且平行于水平面的直线为轴,建立平面直角坐标系,一个水斗从点出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过秒后,水斗旋转到点,设点的坐标为 , 其纵坐标满足 , 当秒时,( )
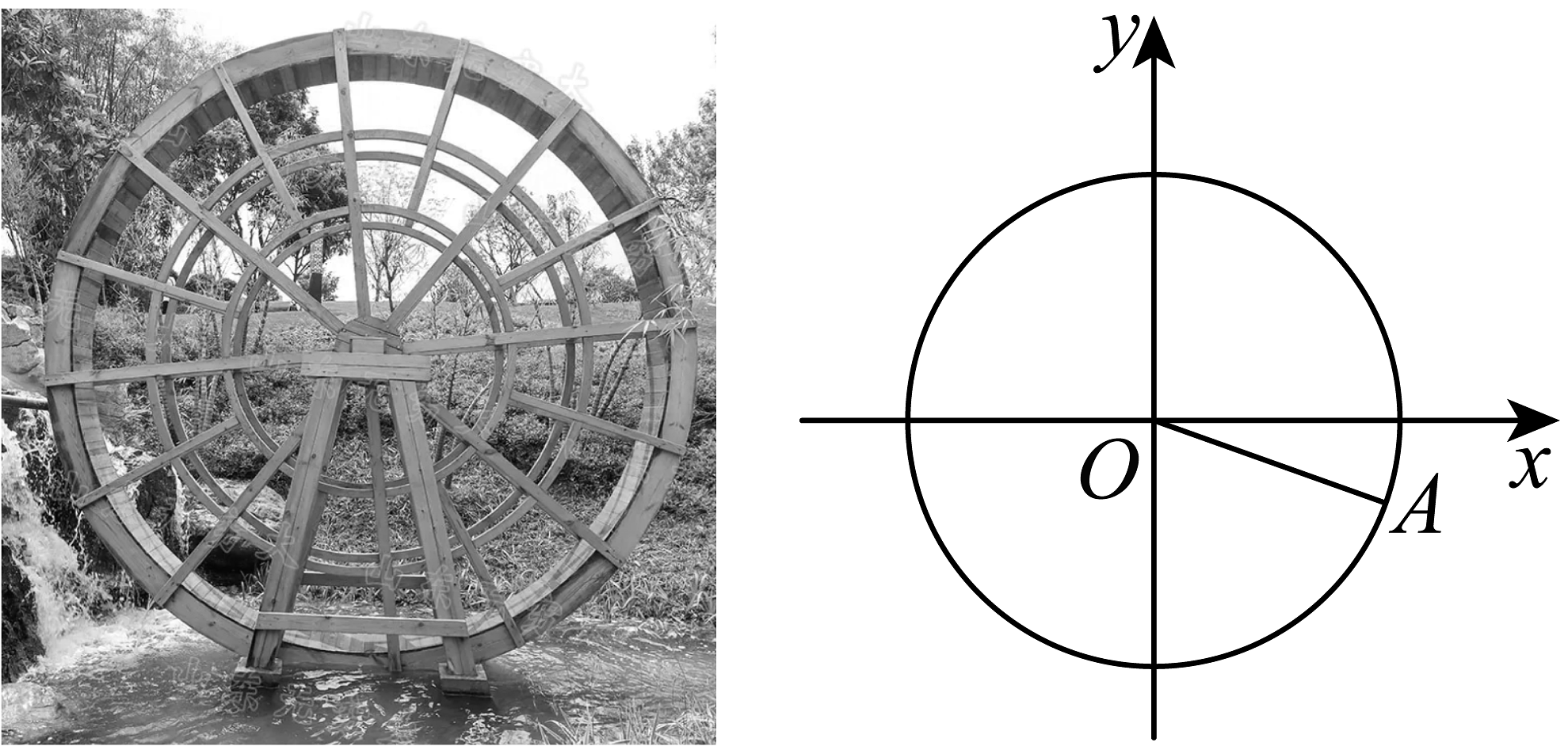 A、 B、 C、 D、4
A、 B、 C、 D、4 -
14、为研究光照时长(小时)和种子发芽数量(颗)之间的关系,某课题研究小组采集了9组数据,绘制散点图如图所示,并对 , 进行线性回归分析.若在此图中加上点后,再次对 , 进行线性回归分析,则下列说法正确的是( )
 A、 , 不具有线性相关性 B、决定系数变大 C、相关系数变小 D、残差平方和变小
A、 , 不具有线性相关性 B、决定系数变大 C、相关系数变小 D、残差平方和变小 -
15、已知复数(其中是虚数单位),则( )A、2 B、1 C、 D、
-
16、在等差数列中,.(1)、求的通项公式;(2)、若数列满足 , 其前项和为 , 证明:数列为等比数列,且(3)、证明:当时, , 数列为正常数)的前项和也为这个数列中的某一项.
-
17、下列说法正确的是( )A、若数列前项和满足 , 则 B、在等差数列中,满足 , 则其前项和中最大 C、在等差数列中,满足 , 则数列的前9项和为定值 D、若等差数列中, , 则使的最大的为15
-
18、已知△ABC是边长为1的正三角形,是BN上一点且 , 则( )A、 B、 C、 D、1
-
19、已知正四棱台的体积为 , 则与底面ABCD所成角的正切值为( )A、 B、 C、 D、4
-
20、已知两个数列和的项数均为 , 且对于数列 , 其中 , 若存在满足:① , 都有;② , 使得 , 则称数列是的单极数列.(1)、已知 , 若的单极数列为 , 求满足条件的的个数.(2)、已知是的单极数列.
(i)若 , 求.
(ii)若 , 当时,证明:.