版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知三棱锥 $P - A B C$ 满足 $A B ⊥ A C, A B ⊥ P B, A C ⊥ P C$ ，且 $A P = 3, B P = \sqrt{5}, B C = 2 \sqrt{2}$ ．

(1)、求证： $A P ⊥ B C$ ；

(2)、求直线 $B C$ 与平面 $A B P$ 所成角的正弦值，

查看解析
2、已知数列 $\{3^{a_{n}}\}$ 是首项为3，公比为9的等比数列，数列 $\{b_{n}\}$ 满足 $b_{1} + \frac{b_{2}}{3} + \frac{b_{3}}{3^{2}} + \dots + \frac{b_{n}}{3^{n - 1}} = 3 n$ .

(1)、求数列 $\{a_{n}\}$ 和 $\{b_{n}\}$ 的通项公式；

(2)、求数列 $\{\frac{a_{n}}{b_{n}}\}$ 的前 $n$ 项和 $S_{n}$ .

查看解析
3、在 $△ A B C$ 中， $∠ A B C = 90 °$ ， $A B = 4$ ， $B C = 3$ ，点 $D$ 在线段 $A C$ 上，若 $∠ B D C = 45 °$ ，则 $B D =$ ； $\cos ∠ A B D =$ .

查看解析
4、设函数 $f (x)$ 与其导函数 $f^{'} (x)$ 的定义域均为 $R$ ，且 $f^{'} (x + 2)$ 为偶函数， $f (1 + x) - f (1 - x) = 0$ ，则（）

A、 $f^{'} (1 + x) = f^{'} (1 - x)$ B、 $f^{'} (3) = 0$ C、 $f^{'} (2025) = 0$ D、 $f (2 + x) + f (2 - x) = 2 f (2)$

查看解析
5、在平行六面体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，已知 $A B = A D = A A_{1} = 1$ ， $∠ A_{1} A B = ∠ A_{1} A D = ∠ B A D = 60 °$ ，则（）

A、直线 $A_{1} C$ 与BD所成的角为90° B、线段 $A_{1} C$ 的长度为 $\sqrt{3}$ C、直线 $A_{1} C$ 与 $B B_{1}$ 所成的角为90° D、直线 $A_{1} C$ 与平面 $A B C D$ 所成角的正弦值为 $\frac{\sqrt{6}}{3}$

查看解析
6、下列说法正确的是（）

A、已知随机变量 $X$ 服从正态分布 $N (μ, σ^{2})$ ， $σ$ 越小，表示随机变量 $X$ 分布越集中 B、数据1，9，4，5，16，7，11，3的第75百分位数为9 C、线性回归分析中，若线性相关系数 $|r|$ 越大，则两个变量的线性相关性越弱 D、已知随机变量 $X ~ B (7, \frac{1}{2})$ ，则 $E (X) = \frac{7}{2}$

查看解析
7、已知函数 $f (x) = \{\begin{array}{l} x e^{x}, x < 1, \\ - x^{2} + 2 x + a, x \geq 1, \end{array}$ 若 $5 f (x) + 1 = 0$ 有3个实数解，则实数 $a$ 的取值范围为（）

A、 $[- \frac{1}{e}, + \infty)$ B、 $[- \frac{6}{5}, + \infty)$ C、 $[- \frac{1}{e}, e]$ D、 $[- \frac{1}{e}, e - 1]$

查看解析
8、已知函数 $f (x) = sin (ω x + φ) (ω > 0, |φ| < \frac{π}{2})$ 满足 $f (\frac{π}{3}) = 1$ ，最小正周期为 $π$ ，函数 $g (x) = sin 2 x$ ，则将 $f (x)$ 的图象向左平移（）个单位长度后可以得到 $g (x)$ 的图象

A、 $\frac{π}{12}$ B、 $\frac{π}{6}$ C、 $\frac{5 π}{6}$ D、 $\frac{11 π}{12}$

查看解析
9、已知等比数列 $\{a_{n}\}$ 的前2项和为12， $a_{1} - a_{3} = 6$ ，则公比 $q$ 的值为（）

A、 $\frac{1}{2}$ B、2 C、 $\frac{1}{3}$ D、3

查看解析
10、已知复数 $z$ 满足 $5 z + 3 \bar{z} = 8 - 2 i$ ，则 $|z| =$ （）

A、1 B、2 C、 $\sqrt{2}$ D、 $2 \sqrt{2}$

查看解析
11、已知集合 $A = \{x |x \geq 1\}$ ， $B = \{x |2 x^{2} - 5 x - 3 < 0\}$ ，则 $A \cup B =$ （）

A、 $\{x |x \geq 1\}$ B、 $\{x |x > - \frac{1}{2}\}$ C、 $\{x |1 < x < \frac{3}{2}\}$ D、 $\{x |1 \leq x < 3\}$

查看解析
12、已知函数 $g (x) = \ln x - a x^{2} + (2 - a) x$ （ $a \in R$ ）．

(1)、求 $g (x)$ 的单调区间；

(2)、若函数 $f (x) = g (x) + a x^{2} - (2 + a) x$ ， $x_{1}, x_{2} (0 < x_{1} < x_{2})$ 是函数 $f (x)$ 的两个零点，证明： $f^{'} (\frac{x_{1} + x_{2}}{2}) < 0$ ．

查看解析
13、设各项非零的数列 $\{a_{n}\}$ 的前n项和记为 $S_{n}$ ，记 $T_{n} = S_{1} \cdot S_{2} \cdot S_{3} \cdot \cdot \cdot \cdot \cdot S_{n}$ ，且满足 $2 S_{n} T_{n} - S_{n} - 2 T_{n} = 0$ ，

(1)、求 $T_{1}$ ， $T_{2}$ 的值，并求数列 $\{T_{n}\}$ 的通项公式；

(2)、设 $c_{n} = a_{n} + \frac{{(- 1)}^{n}}{n a_{n}}$ ，求数列 $\{c_{n}\}$ 的前n项和 $K_{n}$ ．

查看解析
14、随着5G网络信号的不断完善，5G手机已经成为手机销售市场的明星．某地区手机专卖商场对已售出的1000部5G手机的价格数据进行分析得到如图所示的频率分布直方图：

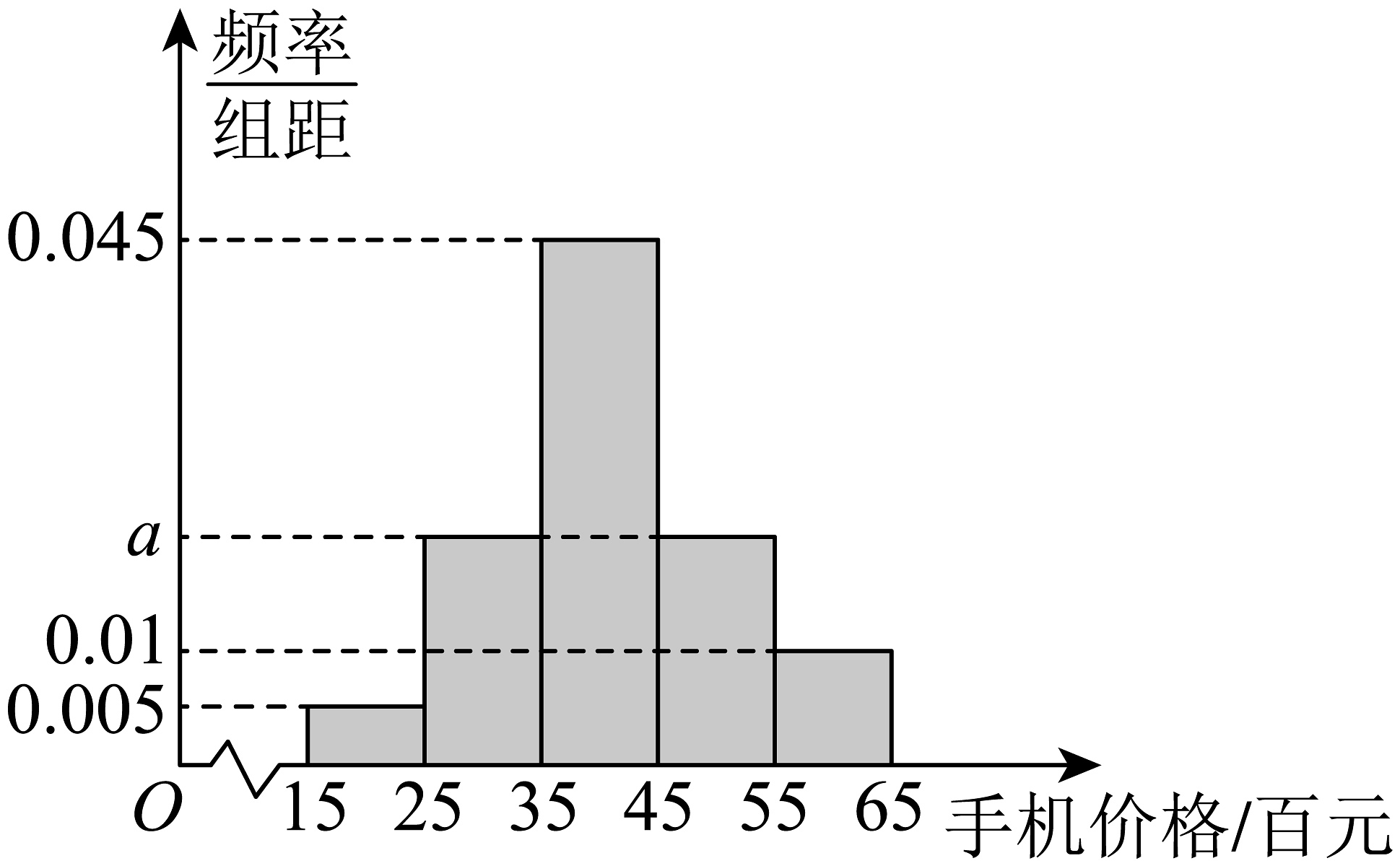(1)、求5G手机的价格75%分位数；

(2)、某夫妻两人到该商场准备购买价位在4500~6500的手机各一部，商场工作人员应顾客的要求按照分层随机抽样的方式提供了9部手机让其从中购买两部，假定选择每部手机是等可能的，设这两人购买同一价位区间的手机的数量为X，求 $E (X)$

查看解析
15、若曲线 $y = ln (x + 1) + x$ 在原点处的切线也是曲线 $y = e^{x} - 2 + a$ 的切线，则 $a =$ ．

查看解析
16、设函数 $f (x) = 2 x^{3} - 3 a x^{2} + 1$ ，则（）

A、存在a，b，使得 $x = b$ 为曲线 $y = f (x)$ 的对称轴 B、存在a，使得点 $(1, f (1))$ 为曲线 $y = f (x)$ 的对称中心 C、当 $a < 0$ 时， $x = a$ 是 $f (x)$ 的极大值点 D、当 $a > 1$ 时， $f (x)$ 有三个零点

查看解析
17、豆瓣评分是将用户评价的一到五星转化为0-10的分值（一星2分，二星4分，三星6分，以此类推），以得分总和除以评分的用户人数所得的数字，国庆爱国影片《长津湖》豆瓣得分是7.4分，截止至2021年10月24日，共计有437181人参与评分，豆瓣评分表如下．根据猫眼实时数据，该片的票房为53.1亿元，按照平均票价50元来计算，大约有1亿人次观看了此片，假如参与评分观众中有97.6%的评价不低于二星，则下列说法正确的是（）

A、m的值是32% B、随机抽取100名观众，则一定有24人评价五星 C、若以频率当作概率，记事件A为“评价是一星”，事件B为“评价不高于二星”，则 $P (B | A) = \frac{8}{37}$ D、若从已作评价的观众中随机抽出3人，则事件“至多1人评价五星”与事件“恰有2人评价五星”是互斥且不对立事件

查看解析
18、已知向量 $\vec{m} = (cos α, sin (π + α))$ ， $\vec{n} = (sin (\frac{π}{2} + β), sin β)$ 则（）

A、 $\vec{m} \cdot \vec{n} = cos (α + β)$ B、 ${\vec{m}}^{2} + {\vec{n}}^{2} = 2$ C、若 $\vec{m} ∥ \vec{n}$ ，则 $α + β = 2 k π (k \in Z)$ D、 $|\vec{m} + \vec{n}| \leq 2$

查看解析
19、设函数 $f (x) = {\begin{matrix} | \ln x |, x > 0 \\ e^{x} (x + 1), x \leq 0 \end{matrix}$ ，若方程 ${[f (x)]}^{2} - a f (x) + \frac{1}{16} = 0$ 有六个不等的实数根，则实数a可取的值可能是（）

A、 $\frac{2}{3}$ B、 $\frac{2}{3}$ 或1 C、1 D、 $\frac{2}{3}$ 或2

查看解析
20、已知椭圆 $E$ ： $\frac{x^{2}}{16} + \frac{y^{2}}{4} = 1$ 的左右顶点分别为 $A_{1}$ ， $A_{2}$ ，圆 $O_{1}$ 的方程为 ${(x + 1)}^{2} + {(y - \frac{\sqrt{3}}{2})}^{2} = \frac{1}{4}$ ，动点 $P$ 在曲线 $E$ 上运动，动点 $Q$ 在圆 $O_{1}$ 上运动，若 $△ A_{1} A_{2} P$ 的面积为 $4 \sqrt{3}$ ，记 $|P Q|$ 的最大值和最小值分别为 $m$ 和 $n$ ，则 $m + n$ 的值为（）

A、 $\sqrt{7}$ B、 $2 \sqrt{7}$ C、 $3 \sqrt{7}$ D、 $4 \sqrt{7}$

查看解析

上一页 698 699 700 701 702 下一页跳转