-
1、已知函数 , , 且 , 则函数可能是( )A、 B、 C、 D、
-
2、从两位数中随机选择一个数,则它的平方的个位数字为1的概率是( )A、 B、 C、 D、
-
3、已知向量 , , 若 , 则( )A、 B、 C、1 D、2
-
4、若 , 则( )A、 B、 C、 D、
-
5、已知函数是定义在上的奇函数,若 , 且 , 都有成立,则不等式的解集为( )A、 B、 C、 D、
-
6、已知曲线上任意一点到点的距离与到直线的距离之比为.(1)、求的方程.(2)、若点在圆上, , 为的两条切线, , 是切点.
(i)求点的纵坐标的取值范围;
(ii)求的面积S的最大值.
附:若曲线的两条切线相交于点 , 则两侧切点所在直线的方程为.
-
7、已知直椭圆柱体是指底面为椭圆,侧面与底面垂直的柱体.如图所示,直椭圆柱体的上下底面椭圆离心率为 , 高为椭圆短轴长度的 , 下底面长轴记为 , 上底面长轴记为 . 点为上一点,过点在下底面内作的垂线分别交下底面椭圆于点 , . 记 .
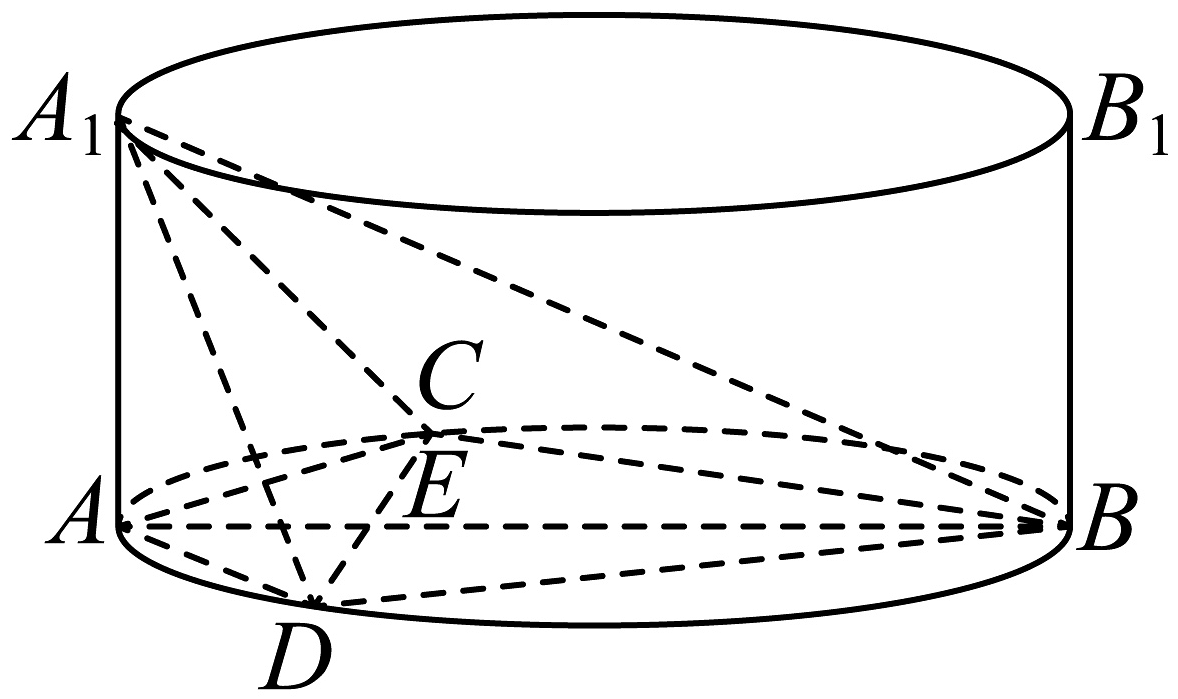 (1)、若平面平面 , 求及二面角的余弦值;(2)、若随变量的变化而变化,且 , . 记二面角的大小为 , 证明: .
(1)、若平面平面 , 求及二面角的余弦值;(2)、若随变量的变化而变化,且 , . 记二面角的大小为 , 证明: . -
8、已知为等差数列,为等比数列且公比大于 , , , ,(1)、求和的通项公式;(2)、设 , 记数列的前项和为 , 求.
-
9、《九章算术》中,将四个面均为直角三角形的四面体称之为鳖臑.如图,平面ABCD, , 四边形ABCD中, , , , .
 (1)、证明:四面体BCFD为鳖臑;(2)、求点C到平面BDF的距离;(3)、求几何体ABCDEF的表面积.
(1)、证明:四面体BCFD为鳖臑;(2)、求点C到平面BDF的距离;(3)、求几何体ABCDEF的表面积. -
10、在中,分别为内角A,B,C的对边,且 .(1)、求C的大小;(2)、若 , 求的面积.
-
11、存在正数使得不等式成立,则的最大值是.
-
12、若数列满足( , 为常数),则称数列为“调和数列”.已知数列为“调和数列”,下列说法正确的是( )A、若 , 则 B、若 , 且 , , 则 C、若中各项均为正数,则 D、若为数列的前项和,且满足 , , 则
-
13、在平面直角坐标系中,过圆外的动点作圆的两条切线,切点为 , 则下列结论正确的有( )A、若点 , 则四边形的面积是 B、若点 , 则四边形的外接圆方程是 C、若点在直线上,则所在圆的直径的最小值是 D、当取得最小值时,点到圆心的距离为
-
14、下列说法中正确的是( )A、若一个经验回归方程为 , 则当变量增加1个单位时,平均增加2个单位 B、已知随机变量 , 若 , 则 C、两组样本数据和 . 若 , 则 D、已知一组样本点的经验回归方程为 , 若样本点与的残差相等,则
-
15、定义在上的函数满足 , 且当时,.则方程所有的根之和为( )A、10 B、12 C、14 D、16
-
16、已知双曲线的通径为线段 , 到双曲线两条渐近线的距离之和等于实轴长,则双曲线的离心率为( )A、 B、 C、 D、
-
17、若 , 则的值为( )A、 B、 C、 D、
-
18、已知集合 , 则( )A、 B、 C、 D、
-
19、已知向量 , , 若 , 则实数( )A、或 B、1或 C、或 D、1或
-
20、已知数列的通项公式为 , 则根据题意,该数列的前4项和( )A、4 B、6 C、8 D、10