-
1、观察下列散点图的分布规律和特点,其中两个变量存在相关关系的有( )A、
 B、
B、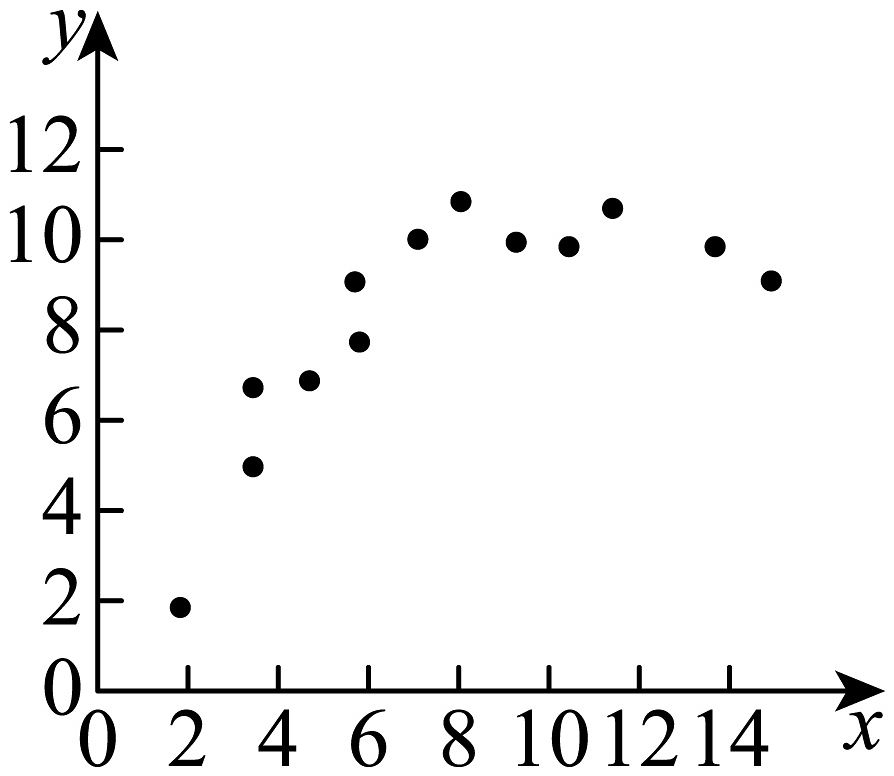 C、
C、 D、
D、
-
2、飞行棋是一种家喻户晓的竞技游戏,玩家根据骰子(骰子为均匀的正六面体)正面朝上的点数确定飞机往前走的步数,刚好走到终点处算“到达”,如果玩家投掷的骰子点数超出到达终点所需的步数,则飞机须往回走超出点数对应的步数.在一次游戏中,飞机距终点只剩3步(如图所示),设该玩家到达终点时投掷骰子的次数为 , 则( )
 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6 -
3、已知函数的值域为 , 则实数的取值范围为( )A、 B、 C、 D、
-
4、已知 , , 则( )A、 B、5 C、 D、
-
5、已知函数f(x)=loga(x+1),g(x)=2loga(2x+t)(t∈R),其中x∈[0,15],a>0,且a≠1.
(1)若1是关于x的方程f(x)﹣g(x)=0的一个解,求t的值;
(2)当0<a<1时,不等式f(x)≥g(x)恒成立,求t的取值范围.
-
6、已知函数.
(1)求的最小正周期;
(2)当时,
(ⅰ)求函数的单调递减区间;
(ⅱ)求函数的最大值、最小值,并分别求出使该函数取得最大值、最小值时的自变量的值.
-
7、如图所示,在三棱柱中,底面为正三角形,在底面上的射影是棱的中点 , 于点.

(1)证明平面;
(2)若 , 求与平面所成角的正弦值.
-
8、已知等比数列的前n项和为 , , 且.
(1)求数列的通项公式;
(2)若数列为递增数列,数列满足 , 求数列的前n项和.
(3)在条件(2)下,若不等式对任意正整数n都成立,求的取值范围.
-
9、已知圆上一定点 , 点为圆内一点,为圆上的动点.(1)、求线段中点的轨迹方程;(2)、若 , 求线段中点的轨迹方程.
-
10、经过原点作函数图像的切线,则切线方程为 .
-
11、计算.
-
12、如图,已知点是平行四边形的边的中点,为边上的一列点,连接交于 , 点满足 , 其中数列是首项为的正项数列,是数列的前项和,则下列结论正确的是( )
 A、 B、数列是等比数列 C、 D、
A、 B、数列是等比数列 C、 D、 -
13、意大利数学家列昂纳多·斐波那契是第一个研究了印度和阿拉伯数学理论的欧洲人,斐波那契数列被誉为是最美的数列,斐波那契数列满足: , , .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前项所占的格子的面积之和为 , 每段螺旋线与其所在的正方形所围成的扇形面积为 , 则下列结论正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、(多选)函数( , , )在一个周期内的图像如图所示,则( )
 A、该函数的解析式为 B、该函数图象的对称中心为 , C、该函数的增区间是 , D、把函数的图像上所有点的横坐标伸长为原来的倍,纵坐标不变,可得到该函数图象
A、该函数的解析式为 B、该函数图象的对称中心为 , C、该函数的增区间是 , D、把函数的图像上所有点的横坐标伸长为原来的倍,纵坐标不变,可得到该函数图象 -
15、已知偶函数对于任意的满足(其中是函数的导函数),则下列不等式中成立的是A、 B、 C、 D、
-
16、函数是A、奇函数且在上单调递增 B、奇函数且在上单调递增 C、偶函数且在上单调减增 D、偶函数且在上单调递增
-
17、函数 的图象大致为A、
 B、
B、 C、
C、 D、
D、
-
18、若数列满足 , , 则数列的前n项和最大时,n的值为( )A、6 B、7 C、8 D、9
-
19、数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.因为运算,数的威力无限;没有运算,数就只是一个符号.对数运算与指数幂运算是两类重要的运算.
(1)对数的运算性质降低了运算的级别,简化了运算,在数学发展史上是伟大的成就.对数运算性质的推导有很多方法.请同学们根据所学知识推导如下的对数运算性质:如果 , 且 , , 那么;
(2)请你运用上述对数运算性质计算的值;
(3)因为 , 所以的位数为4(一个自然数数位的个数,叫做位数).请你运用所学过的对数运算的知识,判断的位数.(注)
-
20、设数列的前项和为 , 且满足 , .
(1)求(用表示);
(2)求证:当时,不等式成立.