-
1、已知的三个内角A,B,C的对边分别是a,b,c, , 则下列说法正确的有( )A、 B、若D为边的中点,且 , 则的面积的最大值为 C、若是锐角三角形,则的取值范围是 D、若角B的平分线与边相交于点E,且的面积 , 则的最大值为
-
2、已知函数的最小正周期为 , 则下列说法正确的有( )A、是图象的一条对称轴 B、在区间上单调递减 C、是图象的一个对称中心 D、在区间的值域为
-
3、下列说法不正确的有( )A、或 B、 C、已知 , 为非零向量,且 , 则与方向相同 D、若 , 则与的夹角是钝角
-
4、下面关于空间几何体叙述正确的有( )A、圆柱的所有母线长都相等 B、底面是正方形的棱锥是正四棱锥 C、一个棱台最少有5个面 D、用一平面去截圆台,截面一定是圆面
-
5、已知向量 , , 满足 , , , , 则的最小值等于( )A、 B、 C、4 D、
-
6、在中,若 , 则的形状是( )A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰或直角三角形
-
7、已知 , , 且 , 的夹角为 , 则( )A、1 B、 C、2 D、
-
8、如图,在平行四边形中,E、F分别是边上的两个三等分点,则下列选项错误的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
9、在平面直角坐标系中,角的顶点在原点,始边与x轴的非负半轴重合,终边经过点 , 则( )A、 B、 C、1 D、5
-
10、在中,A,B,C所对的边分别为a,b,c,已知 , , , 则角C的大小为( )A、45° B、105°或15° C、15° D、135°或45°
-
11、( )A、 B、 C、 D、
-
12、已知为有穷整数数列,共有项.给定正整数 , 若对任意的 , 在中,存在 , 使得 , 表示中最大的一项,表示中最小的一项,则称为有界数列.(1)、判断是否为有界数列,判断是否为有界数列,说明理由;(2)、若共有4项, , 且为单调递增数列,写出所有的 , 使得为有界数列;(3)、若为有界数列,证明: .
-
13、在正三棱柱中,已知 , 点 , 分别为和的中点,点是棱上的一个动点,则下列说法中正确的有( )A、存在点 , 使得平面 B、直线与为异面直线 C、存在点 , 使得 D、存在点 , 使得直线与平面的夹角为45°
-
14、如图,已知向量 , 可构成空间向量的一个基底,若 , , . 在向量已有的运算法则的基础上,新定义一种运算 , 显然的结果仍为一向量,记作
 (1)、求证:向量为平面OAB的法向量;(2)、若 , , 求以OA,OB为边的平行四边形OADB的面积,并比较四边形OADB的面积与的大小;(3)、将四边形OADB按向量平移,得到一个平行六面体 , 试判断平行六面体的体积V与的大小.(注:第(2)小题的结论可以直接应用)
(1)、求证:向量为平面OAB的法向量;(2)、若 , , 求以OA,OB为边的平行四边形OADB的面积,并比较四边形OADB的面积与的大小;(3)、将四边形OADB按向量平移,得到一个平行六面体 , 试判断平行六面体的体积V与的大小.(注:第(2)小题的结论可以直接应用) -
15、已知圆 , 直线是圆与圆的公共弦AB所在直线,且圆的圆心在直线上.(1)、求公共弦AB的长度;(2)、求圆的方程;(3)、过点分别作直线 , , 交圆于 , , , 四点,且 , 试探究是否为定值,若为定值,请求出该定值;若不为定值,请说明理由.
-
16、如图,在长方体中,分别为棱 , 的中点.
 (1)、证明:四点共面;(2)、为边上一点,若平面与平面ABCD所成夹角的余弦值为 , 求CP的长度.
(1)、证明:四点共面;(2)、为边上一点,若平面与平面ABCD所成夹角的余弦值为 , 求CP的长度. -
17、已知点在椭圆上,过点作斜率为1的直线与椭圆交于A,B两点.(1)、求椭圆C的方程;(2)、求的值.
-
18、已知三角形的三个顶点是.(1)、求边AC所在直线的斜截式方程;(2)、求边AC上的高所在直线的斜截式方程.
-
19、设有一组圆 , 存在定直线始终与圆相切.
-
20、布达佩斯的伊帕姆维泽蒂博物馆收藏的达芬奇方砖在正六边形上画了具有视觉效果的正方体图案,如图1,把三片这样的达芬奇方砖拼成图2的组合,这个组合再转换成图3所示的几何体.若图3中每个正方体的棱长为 , 则( )
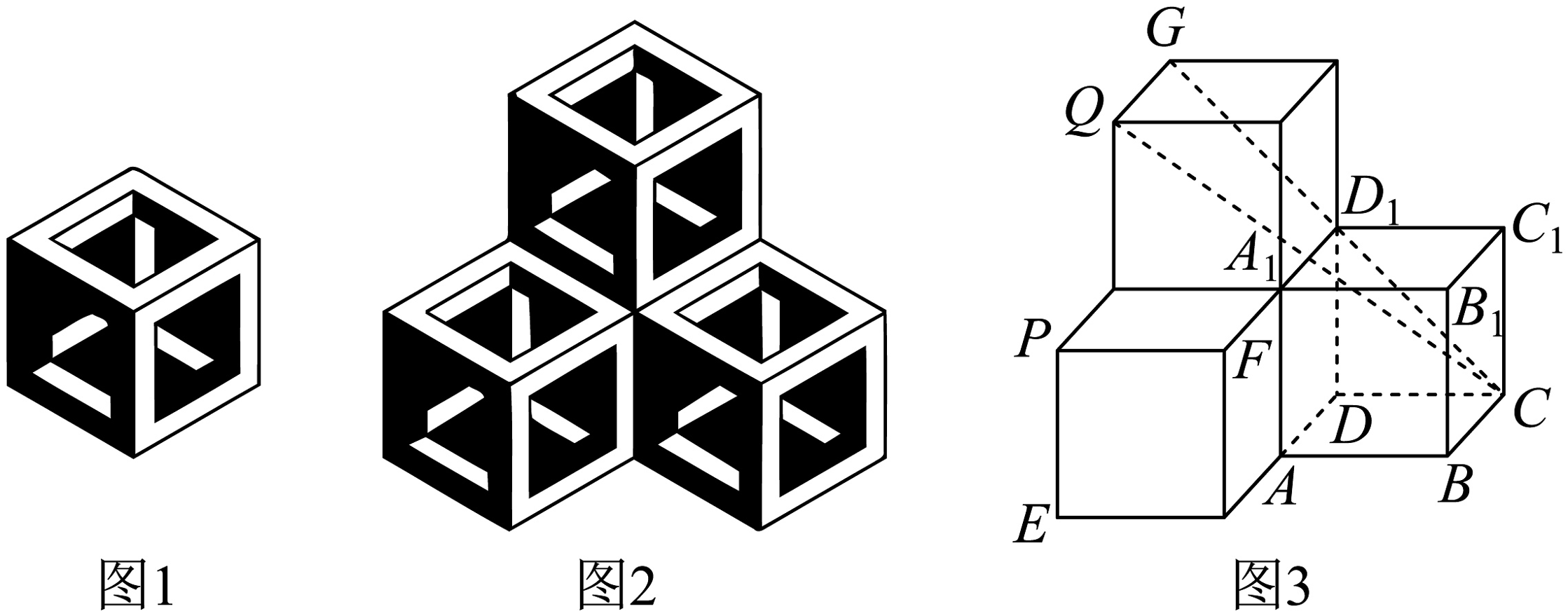 A、点到直线的距离是 B、异面直线与所成角的余弦值为 C、直线到平面的距离是 D、直线与平面所成角的正弦值为
A、点到直线的距离是 B、异面直线与所成角的余弦值为 C、直线到平面的距离是 D、直线与平面所成角的正弦值为