-
1、(1)计算:;
(2)若 , 用表示 .
-
2、已知是定义在上的偶函数,且 , 恒成立,若 , 则满足的实数的取值范围是.
-
3、已知函数 , 将的图像上所有点的横坐标缩短为原来的 , 纵坐标不变,得到函数的图像.已知在上恰有5个零点,则的取值范围是.
-
4、已知 , 若是的充分条件,则实数的取值范围是.
-
5、已知函数 , 若存在四个实数 , , , , 使得 , 则( )A、的范围为 B、的取值范围为 C、的取值范围为 D、的取值范围为
-
6、已知 , 且 , 则下列不等式中正确的是( )A、 B、 C、 D、
-
7、已知函数 , 则( )A、的最小正周期为 B、的值域为 C、的图象关于直线对称 D、有1个零点是
-
8、已知定义在集合上的函数满足.记的最小值为 , 最大值为 , 若集合 , 设表示集合中元素的个数,则下列命题一定正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
9、已知为锐角,且 , , 则角等于( )A、 B、 C、 D、
-
10、著名数学家欧拉曾研究过素数分布问题,并得到不超过整数的素数个数可以近似地表示为的结论.根据该结论,估计10000以内的素数的个数约为( )
(参考数据: , 这里为自然对数的底数)
A、1086 B、2172 C、4343 D、5756 -
11、若 , 则的最小值为( )A、2 B、 C、4 D、5
-
12、已知角的终边经过点 , 则( ).A、3 B、 C、 D、
-
13、已知函数是奇函数,则( )A、0 B、1 C、 D、2
-
14、命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,
-
15、对于定义域为的函数 , 如果存在区间 , 同时满足:①在上是单调函数;②当时, , 则称是该函数的“优美区间”.(1)、求证:是函数的一个“优美区间”;(2)、求证:函数不存在“优美区间”;(3)、已知函数有“优美区间” , 当取得最大值时求的值.
-
16、文明城市是反映城市整体文明水平的综合性荣誉称号.作为普通市民,既是文明城市的最大受益者,又是文明城市的主要创造者.六盘水市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛(满分100分),从所有答卷的成绩中抽取了容量为100的样本,将样本(成绩均为不低于50分的整数)分成五段:得到如图所示的频率分布直方图.
 (1)、求频率分布直方图中的值和估计样本的下四分位数;(2)、按照分层抽样的方法,从样本中抽取20份成绩,应从中抽取多少份;(3)、已知落在的平均成绩是53,方差是4;落在的平均成绩为65,方差是7,求成绩落在的平均数和方差.
(1)、求频率分布直方图中的值和估计样本的下四分位数;(2)、按照分层抽样的方法,从样本中抽取20份成绩,应从中抽取多少份;(3)、已知落在的平均成绩是53,方差是4;落在的平均成绩为65,方差是7,求成绩落在的平均数和方差.(注:若将总体划分为若干层,随机抽取两层,通过分层随机抽样,每层抽取的样本量、样本平均数和样本方差分别为:.记这两层总的样本平均数为 , 样本方差为 , 则)
-
17、如图,直三棱柱中,分别是的中点,.
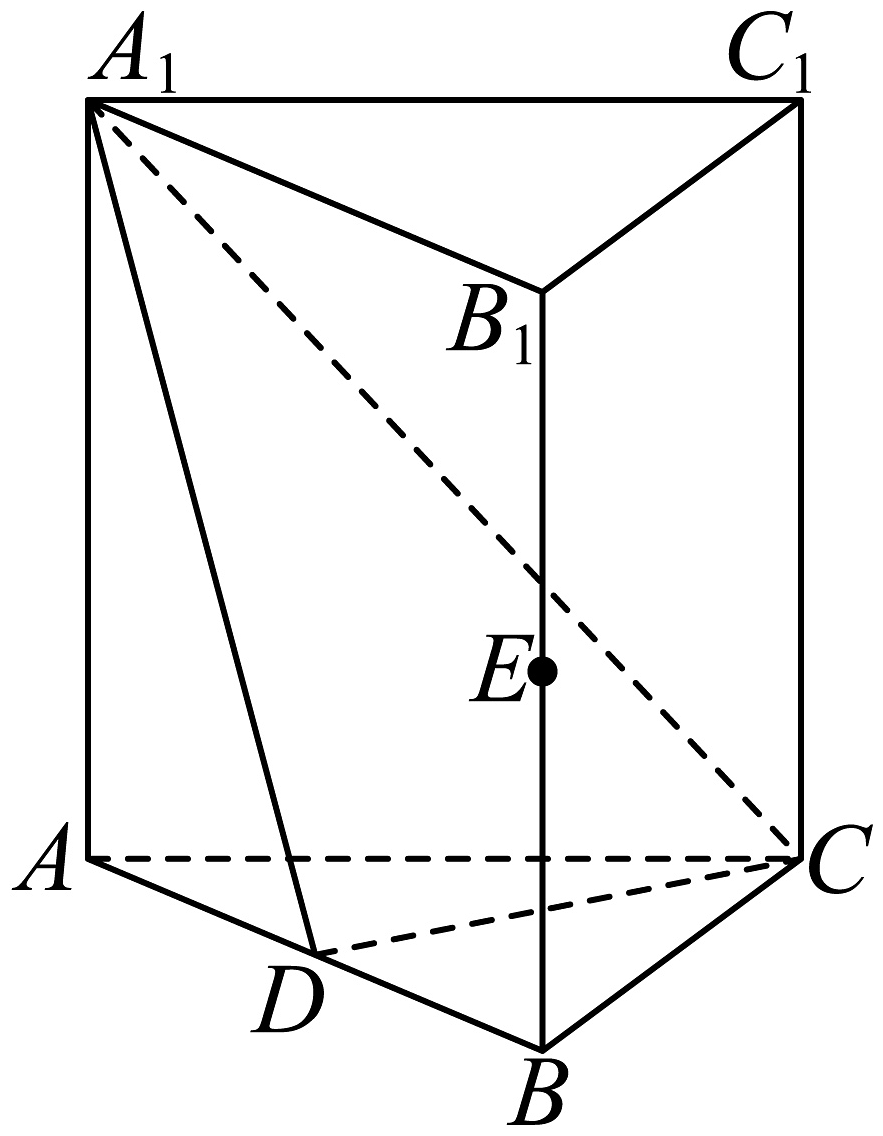 (1)、证明:平面;(2)、求直线与平面所成角的正弦值.
(1)、证明:平面;(2)、求直线与平面所成角的正弦值. -
18、已知函数 ,(1)、求函数的最小正周期;(2)、将函数图象上所有点的横坐标伸长到原来的2倍,纵坐标不变;再向左平移个单位长度,得到函数的图象.当时,求函数的最值.
-
19、已知二次函数的图象经过点且对称轴为.(1)、求的解析式;(2)、求不等式的解集.
-
20、已知分别为三个内角的对边,且 , 则面积的最大值是.