-
1、已知函数 .(1)、讨论的单调性;(2)、当时,求证: .
-
2、设函数.(1)、求曲线在处的切线方程;(2)、求的单调区间与极值;(3)、求出方程的解的个数.
-
3、若 , 求:(1)、求的值;(2)、;(3)、 .
-
4、已知函数在处取得极小值5.(1)、求实数a,b的值;(2)、当时,求函数的最大值.
-
5、若函数在上单调递增,则实数的最大值为 .
-
6、已知函数 , 其导函数的图象如图所示,则对于函数的描述正确的是( )
 A、在上单调递减 B、在处取得极大值 C、在上单调递减 D、在处取得最小值
A、在上单调递减 B、在处取得极大值 C、在上单调递减 D、在处取得最小值 -
7、定义在上的奇函数 , 其导函数为 , , 当时, , 则使得成立的的取值范围是( )A、 B、 C、 D、
-
8、若的展开式中的系数为30,则 ( )A、 B、 C、 D、
-
9、已知事件 , , 若 , 且 , , 则下列结论正确的是( )A、 B、 C、 D、
-
10、若曲线在点处的切线与直线垂直,则a的值为( )A、 B、 C、 D、
-
11、某研究性学习小组有4名男生和4名女生,一次问卷调查活动需要挑选3名同学参加,其中至少一名女生,则不同的选法种数为( )A、120种 B、84种 C、52种 D、48种
-
12、函数在上的最大值是( )A、 B、0 C、 D、
-
13、函数的单调递减区间是( )A、 B、 C、 D、
-
14、函数在时的瞬时变化率为( )A、0 B、2 C、4 D、6
-
15、已知函数的定义域为 , 且对任意 , 满足 , 且则下列结论一定正确的是( )A、 B、 C、 D、
-
16、如图,往一个正四棱台密闭容器内倒入的水,水面高度恰好为棱台高度的 , 且 , , 则这个容器的容积为( )
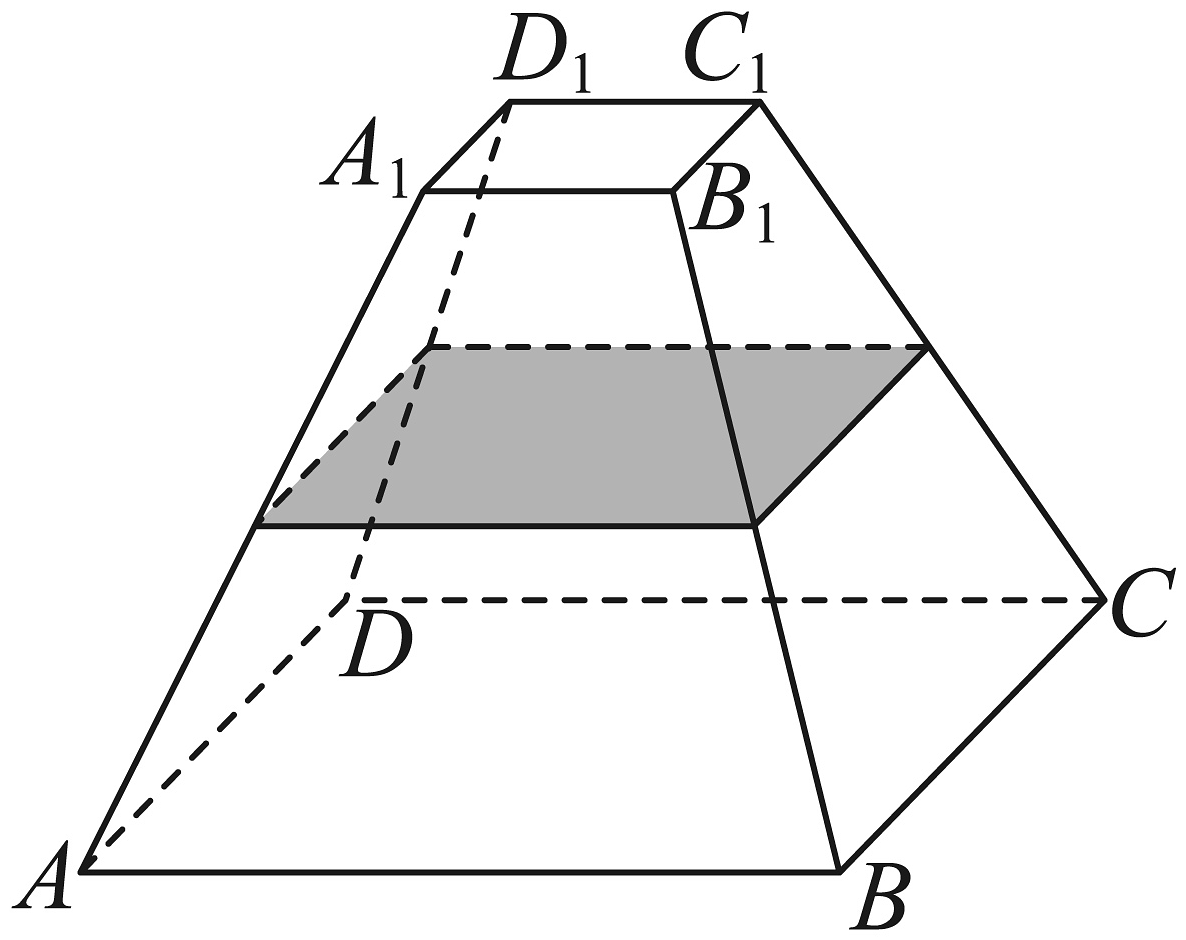 A、 B、 C、 D、
A、 B、 C、 D、 -
17、设函数 .(1)、当时,求的单调区间;(2)、当时,求的取值范围;(3)、若存在 , 使得关于的不等式恒成立,求实数的取值范围.
-
18、中,角A,B,C的对边分别为a,b,c, .(1)、求角B;(2)、设的垂心为H,若 .
(i)求的值;
(ii)求的值.
-
19、如图,中, , , D为中点,E为上一点,且 , 设 , .
 (1)、请用 , 来表示 , ;(2)、若 , 求的值;(3)、当时,求与夹角的余弦值.
(1)、请用 , 来表示 , ;(2)、若 , 求的值;(3)、当时,求与夹角的余弦值. -
20、已知函数 .(1)、求的定义域;(2)、判断的奇偶性并给予证明;(3)、求关于的不等式的解集.