-
1、已知圆锥的轴截面是一个边长为的正三角形,则圆锥的体积为( )A、 B、 C、 D、
-
2、已知复数 , 则( )A、 B、 C、 D、
-
3、若集合 , 则( )A、 B、 C、 D、
-
4、的展开式中的系数为( )A、2 B、6 C、4 D、-4
-
5、已知数列的首项为14,且 , 则的最小值为.
-
6、若空间向量 , , 则( )A、 B、 C、 D、
-
7、若复数z在复平面中的对应点都在一个以原点为圆心的圆上,则的对应点均在( )A、一条直线上 B、一个圆上 C、一条抛物线上 D、一支双曲线上
-
8、设随机变量 , 且 . 若8名团员中有名男生,从这8人中选出4名代表,记选出的代表中男生的人数为Y,则 .
-
9、如图,在中, , 过点的直线分别交直线 , 于不同的两点 , .设 , , 其中 , 则的最小值为( )
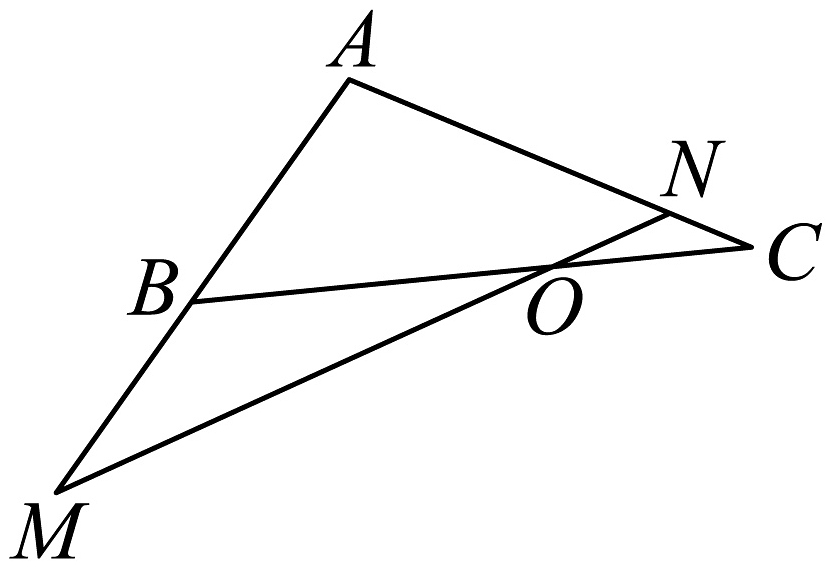 A、 B、 C、 D、
A、 B、 C、 D、 -
10、已知一组数 , , , 的平均数是3,方差为4,则数据 , , , 的平均数和方差分别是( )A、7,8 B、7,16 C、6,8 D、6,16
-
11、如图所示,是的一条中线,点满足 , 过点的直线分别与射线 , 射线交于两点.
 (1)、用和表示;(2)、设 , 实数 , 求的值;(3)、如果是边长为的等边三角形,求的取值范围.
(1)、用和表示;(2)、设 , 实数 , 求的值;(3)、如果是边长为的等边三角形,求的取值范围. -
12、已知向量 , ,(1)、若与夹角为 , 求;(2)、若 , 求的坐标;(3)、若与夹角为 , 求取最小值时的值.
-
13、内角的对边分别为 , 已知 .(1)、求角;(2)、若 , 的面积为 . 求的周长.
-
14、已知是关于的方程的一个根,其中为实数.(1)、求的值;(2)、设复数满足是纯虚数,求实数的值.
-
15、文壁巽塔位于桐乡市崇福镇中山公园,始建于明嘉靖年间,历经劫难不屈不折,现为桐乡市级重点保护文物.在湖对岸为测量塔的高度 , 可以选取与塔底在同一水平面内的两个测量基点与 , 现测得 , 米,在点测得塔顶的仰角为 , 则塔高米.

-
16、已知长方体的长宽高分别为 , , , 现将该长方体沿相邻三个面的对角线截掉一个棱锥,得到如图所示的几何体,则该几何体体积为 .

-
17、已知 , 且与共线,则实数的值为 .
-
18、在中,角的边分别为 , 已知 , 则下列说法正确的是( )A、若 , 则 B、若 , 则 C、周长的最大值为 D、面积的最大值
-
19、已知复数:满足 , 则( )A、 B、的实部为1 C、的共轭复数为 D、在复平面中对应的点位于第四象限
-
20、下列命题错误的是( )A、两两相交且不共点的三条直线确定一个平面 B、四边形可以确定一个平面 C、经过同一直线上的3个点的平面有且仅有3个 D、经过两条平行直线,有且只有一个平面