-
1、已知函数在上单调递减,则实数的取值范围是( )A、 B、 C、 D、
-
2、球面上有三点 , 若 , 且球心到所在平面的距离等于球的半径的一半,则该球的表面积为( )A、 B、 C、 D、
-
3、已知平面向量满足 , 则( )A、-2 B、2 C、-4 D、4
-
4、已知 , 若(为虚数单位)是实数,则( )A、 B、2 C、 D、3
-
5、已知集合 , 集合 , 则( )A、 B、 C、 D、
-
6、已知抛物线的顶点在坐标原点处,对称轴为轴,且过点 , , 是上两个动点.(1)、求抛物线的标准方程;(2)、已知是上一点,且的焦点为的重心,设的横坐标为 , 求的取值范围;(3)、已知为直线在第二象限内一点,直线 , 与抛物线分别相切于 , 两点,设 , 与轴分别交于 , 两点,证明:直线与直线的交点在定直线上.
-
7、已知函数().(1)、设 , 当时, , 求的取值范围.(2)、当时,
①写出曲线的两条相互垂直的切线方程,并说明理由;
②设 , 数列满足 , , 证明: .
-
8、如图,在梯形中, , , , , , 分别为线段 , 上异于端点的一点, , 将梯形沿翻折至与梯形垂直的位置,得到多面体 .
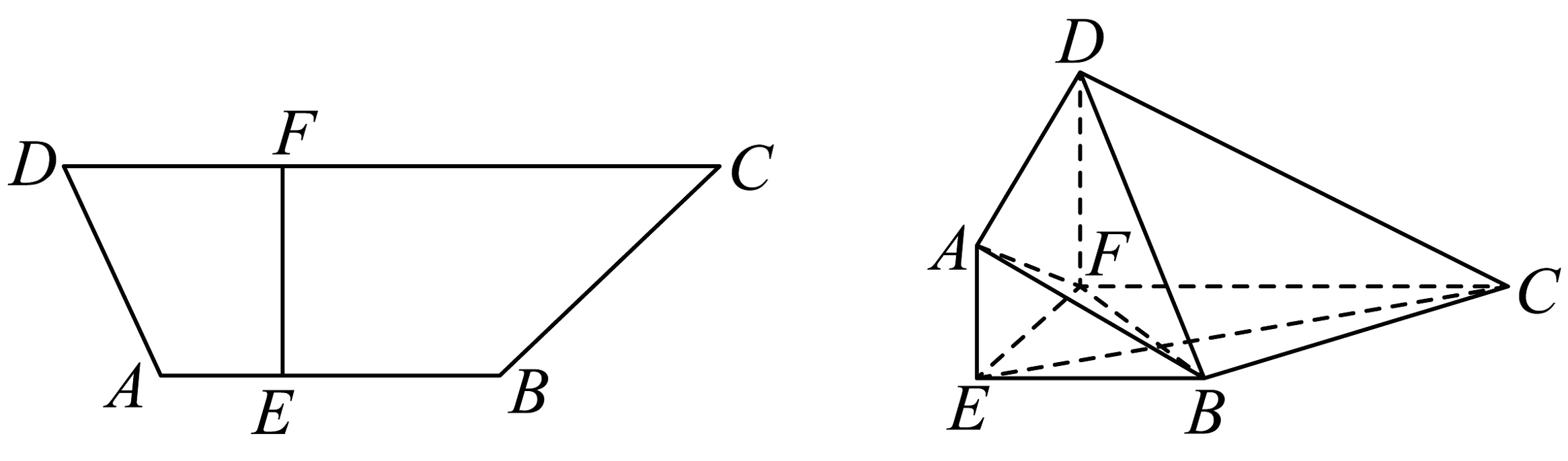 (1)、若 , 证明: .(2)、若平面 , 求直线与平面所成角的正弦值.
(1)、若 , 证明: .(2)、若平面 , 求直线与平面所成角的正弦值. -
9、在制造业智能化的趋势下,某企业委托机构随机调查了200名传统质检员,以评估质检系统对传统质检员数量的影响,部分数据如下表所示:
质检系统的应用情况
传统质检员数量
合计
减少
未减少
应用
70
应用
未应用
50
未应用
合计
100
合计
(1)、根据以上数据及小概率值的独立性检验,能否认为质检系统的应用与传统质检员数量减少有关?(2)、该企业引入质检系统后,将对质检员开展三轮专项培训,已知每轮达到“熟练操作质检系统”水平(视为达标)的概率分别为 , , , 各轮结果相互独立,且规定两轮及以上达标者,方可操作该系统.①某部门有48名质检员,规定培训通过(两轮及以上达标)者可获得500元奖金,求该部门为员工培训需准备的奖金总额的数学期望.
②调研发现,能操作质检系统的质检员中,70%的人薪资涨幅超过15%;不能操作质检系统的质检员中,30%的人薪资涨幅超过15%.若在质检员培训后,从中随机选取一人,其薪资涨幅超过15%,求该员工能操作质检系统的概率.
附: , .
0.050
0.010
0.001
3.841
6.635
10.828
-
10、在中,角的对边分别为 , .(1)、求;(2)、若的面积为 , , 求的周长.
-
11、已知函数有零点,则的最小值为 .
-
12、已知是椭圆的一个焦点,分别是椭圆的长轴与短轴的一个端点,若以为直径的圆经过的中点,则椭圆的离心率为 .
-
13、的展开式中的系数为 .
-
14、已知有穷数列的通项公式为 , 其项数不少于4项,从中选取项组成数列 , 数列满足 , , 则( )A、数列是单调数列 B、当时, C、当时, D、数列的个数为
-
15、已知 , 分别是双曲线:( , )的左、右焦点,为双曲线右支上一点,的最小值为1,且当轴时, , 则( )A、双曲线的焦距为4 B、双曲线的一条渐近线被圆:截得的弦长为2 C、过点作双曲线的一条渐近线的垂线,垂足为 , 则 D、为圆:上一点,的最大值为3
-
16、设函数 , 则下列说法正确的是( )A、的最大值为 B、在上单调递增 C、 , 在上存在极值点 D、的图象向右平移个单位长度后得到的图象对应的函数为偶函数
-
17、已知 , , , 是球的球面上四点, , , , . 记球的体积为 , 四面体的体积为 , 则的值为( )A、 B、 C、 D、
-
18、已知函数满足 , , 则( )A、3 B、 C、5 D、
-
19、已知不共线的向量 , 满足 , , , 则的最小值为( )A、 B、2 C、 D、
-
20、已知函数图象上不同的两点 , 到直线的距离相等,则( )A、 B、 C、 D、