-
1、若函数( , 且)是偶函数,且 , 则.
-
2、已知是球的球面上两点,为该球面上的动点,球的半径为4, , 二面角的大小为 , 则( )A、是钝角三角形 B、直线与平面所成角为定值 C、三棱锥的体积的最大值为 D、三棱锥的外接球的表面积为
-
3、瑞士著名数学家欧拉在1765年提出:三角形的外心,重心,垂心位于同一直线上,这条直线被后人称为三角形的“欧拉线”.若的三个顶点坐标分别为 , , 其“欧拉线”为 , 圆 , 则( )A、过作圆的切线,切点为 , 则的最小值为4 B、若直线被圆截得的弦长为2,则 C、若圆上有且只有两个点到的距离都为1,则 D、存在 , 使圆上有三个点到的距离都为1
-
4、一组成对样本数据的散点位于一条直线附近,它的样本相关系数(其中),由最小二乘法求得经验回归方程(其中),则( )A、若 , 则 B、若 , 则成对数据的样本相关系数等于 C、若 , 则成对数据的样本相关系数大于 D、若 , 则成对数据的经验回归方程
-
5、已知函数在上的所有极值点从小到大依次记为 , 则( )A、 B、 C、 D、
-
6、已知椭圆的左,右焦点分别为 , 过的直线与相交于两点,且 , 则的离心率为( )A、 B、 C、 D、
-
7、已知函数若函数恰有2个零点,则实数的取值范围是( )A、 B、 C、 D、
-
8、已知 , 则( )A、 B、 C、2 D、3
-
9、的展开式中的系数为( )A、24 B、 C、 D、
-
10、声强级(单位:dB)由公式给出,其中为声强(单位:).轻柔音乐的声强一般在之间,则轻柔音乐的声强级范围是( )A、 B、 C、 D、
-
11、已知复数满足 , 则的最小值为A、0 B、1 C、2 D、3
-
12、设集合 , , 则的元素个数为( )A、4 B、3 C、2 D、1
-
13、已知有穷等差数列的公差d大于零.(1)、证明:不是等比数列;(2)、是否存在指数函数满足:在处的切线的交轴于 , 在处的切线的交轴于 , …,在处的切线的交轴于?若存在,请写出函数的表达式,并说明理由;若不存在,也请说明理由;(3)、若数列中所有项按照某种顺序排列后可以构成等比数列 , 求出所有可能的m的取值.
-
14、已知椭圆的右焦点为 , 分别为椭圆的左、右顶点,分别为椭圆的上、下顶点,四边形的面积为 .(1)、求椭圆的方程;(2)、过点且斜率不为的直线与椭圆相交于两点,直线与的交点为 .
①若直线的倾斜角为 , 求线段的长度;
②试问是否有最大值?如果有,求出的最大值;如果没有,说明理由.
-
15、如图,在四棱锥中,棱平面 , 底面四边形是矩形, , 点为棱的中点,点在棱上,.
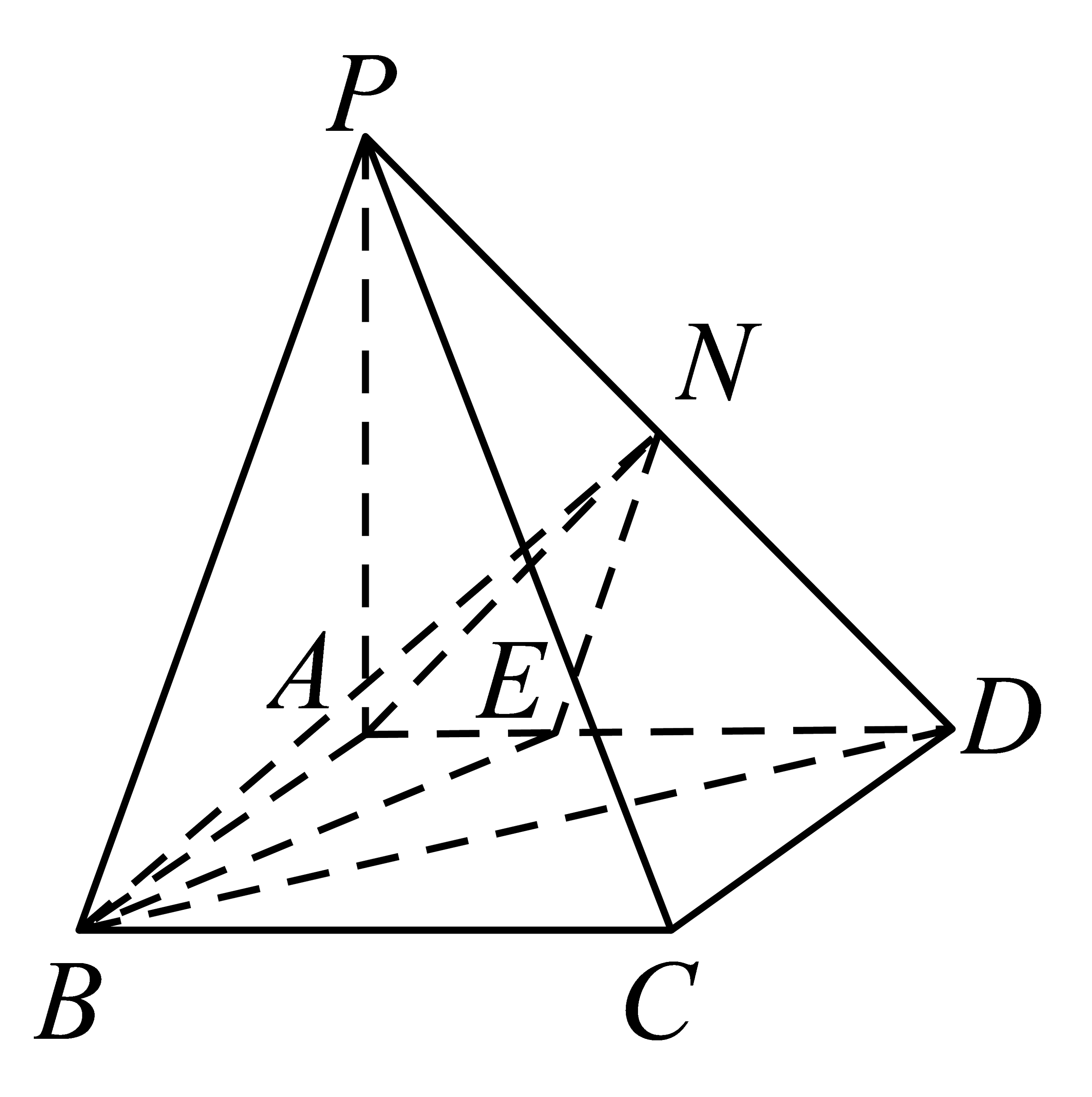 (1)、求证:;(2)、已知平面与平面的交线与直线所成角的正切值为 , 求二面角的余弦值.
(1)、求证:;(2)、已知平面与平面的交线与直线所成角的正切值为 , 求二面角的余弦值. -
16、已知双曲线的右焦点为 , 以(为坐标原点)为直径的圆与的渐近线的一个交点为 , 若 , 则双曲线的离心率为 .
-
17、某中学2025年度青年教师讲题比赛分为文科、理科两个组别进行.文科组和理科组分别有4位和5位教师参赛.根据比赛规则,要求共评出一等奖4名,一等奖中的最高分设为特等奖,其余均为二等奖,且每个组至少有1名一等奖(包含一等奖中的特等奖).则最终的可能比赛结果共有种.
-
18、已知函数 , 若 , 则.
-
19、已知函数且且 , 则下列选项中正确的是( )A、当时,若在区间恒成立,则实数的取值范围为 B、当(e为自然对数的底数)时,的最小值为2 C、当(e为自然对数的底数)时,若恒成立,则实数的最小值为 D、当时,若函数有两个不同的零点,则实数的取值范围为
-
20、的内角的对边分别为 , 且 , , 边的中线 , 则下列结论正确的有( )A、 B、 C、的面积为 D、的外接圆的面积为