-
1、已知数列满足 , .(1)、求证:数列是等差数列;(2)、若且 , 求数列的前项和.
-
2、已知等差数列的前项和为 , 且满足: , .
(1)求数列的通项公式;
(2)记数列的前项和为 , 求取得最大值时的值.
-
3、已知数列{an}中,an+2 , 且m∈R , a1=1,a2=2,a8=16,则{an}的前2n项和S2n=.
-
4、在等比数列中, , , 则.
-
5、已知数列的前项和为 , 下列说法正确的是( )A、若 , 则是等差数列 B、若是等比数列,且 , , 则 C、若是等差数列,则 D、若 , 则是等比数列
-
6、已知数列的前项和为 , 若 , 则下列说法正确的是( )A、是递增数列 B、数列是递增数列 C、数列中的最小项为 D、、、成等差数列
-
7、已知数列满足: , 若对任意恒成立,则实数a的取值范围是( )A、 B、 C、 D、
-
8、设分别为等比数列 , 的前项和,若 , 则( )A、 B、 C、 D、
-
9、在正项等比数列中, , 前三项的和为7,若存在使得 , 则的最小值为( )A、 B、 C、 D、
-
10、在数列中, , , 且 , , 则p,q的值分别为( ).A、 , 6 B、2,1 C、 , 6或2,1 D、 , 7
-
11、已知为等差数列的前n项和,若 , =21,则的值为A、6 B、7 C、8 D、9
-
12、某电动车公司为了抢占更多的市场份额,计划加大广告投入.该公司第i年的年广告费(单位:百万元)满足递推关系 , 且 , 年销售量(单位:百万辆)与年广告费相关.令 , 经过数据处理得到如下统计量的值:
44
4.8
10
40.3
1.612
19.5
8.06
现有模型作为年销售量y关于年广告费x的回归分析模型,其中均为常数.
(1)、求;(2)、求出y关于x的回归方程,并预测年广告费为6(百万元)时,产品的年销售量是多少?(3)、该公司生产的电动车毛利润为每辆200元(不含广告费、研发经费).该公司在加大广告投入的同时也加大研发经费的投入,年研发经费为年广告费的199倍.电动车的年净利润受年广告费和年研发经费影响外还受随机变量影响,设随机变量服从正态分布 , 且满足 , 求该公司年净利润的最大值大于1000(百万元)的概率.(年净利润=毛利润×年销售量-年广告费-年研发经费-随机变量)附:①回归直线
②参考数据: , .
-
13、已知双曲线 . 点在上.按如下方式构造点 . 过点作斜率为的直线与的下支交于点 . 点关于轴的对称点为 . 记点的坐标为(1)、求的值:(2)、记 . 证明:数列为等比数列;(3)、记的面积为 . 证明:是定值.
-
14、第十五届全国运动会将于2025年在广东、香港、澳门三地举办.为了普及全运知识.某中学举办了一次全运知识闯关比赛.比赛分为初赛与复赛.初赛胜利后才能进入复赛.初赛规定:三人组队参赛.每次只派一个人.且每人只派一次:如果一个人闯关失败.再派下一个人重新闯关:三人中只要有人闯关成功即视作初赛胜利.无需继续闯关.现有甲、乙、丙三人组队参加初赛.他们各自闯关成功的概率分别为 . 假定互不相等.且每人能否闯关成功相互独立.(1)、若计划依次派甲、乙、丙进行初赛闯关. . 求该小组初赛胜利的概率:(2)、已知 . 现有两种初赛人员派出方案:
方案一:依次派出甲乙丙:
方案二:依次派出丙乙甲
设方案一和方案二派出人员数目分别为随机变量 . 求 . 并比较它们的大小;
(3)、初赛胜利小组的三名成员都可以进入复赛.复赛规定:单人参赛.每个人回答三道题.全部答对获得一等奖:答对两道题获得二等奖:答对一道题获得三等奖:全部答错不获奖.已知某学生进入了复赛.该学生在复赛中前两道题答对的概率均为 . 第三道题答对的概率为 . 若该学生获得一等奖的概率为 , 设该学生获得二等奖的概率为 . 求的最小值. -
15、已知函数.(1)、当时,求曲线在处的切线方程;(2)、讨论函数的单调性.(3)、若存在极大值,且极大值不大于 , 求实数的取值范围.
-
16、如图所示,在等腰直角中, , 点、分别为的中点,将沿翻折到位置.
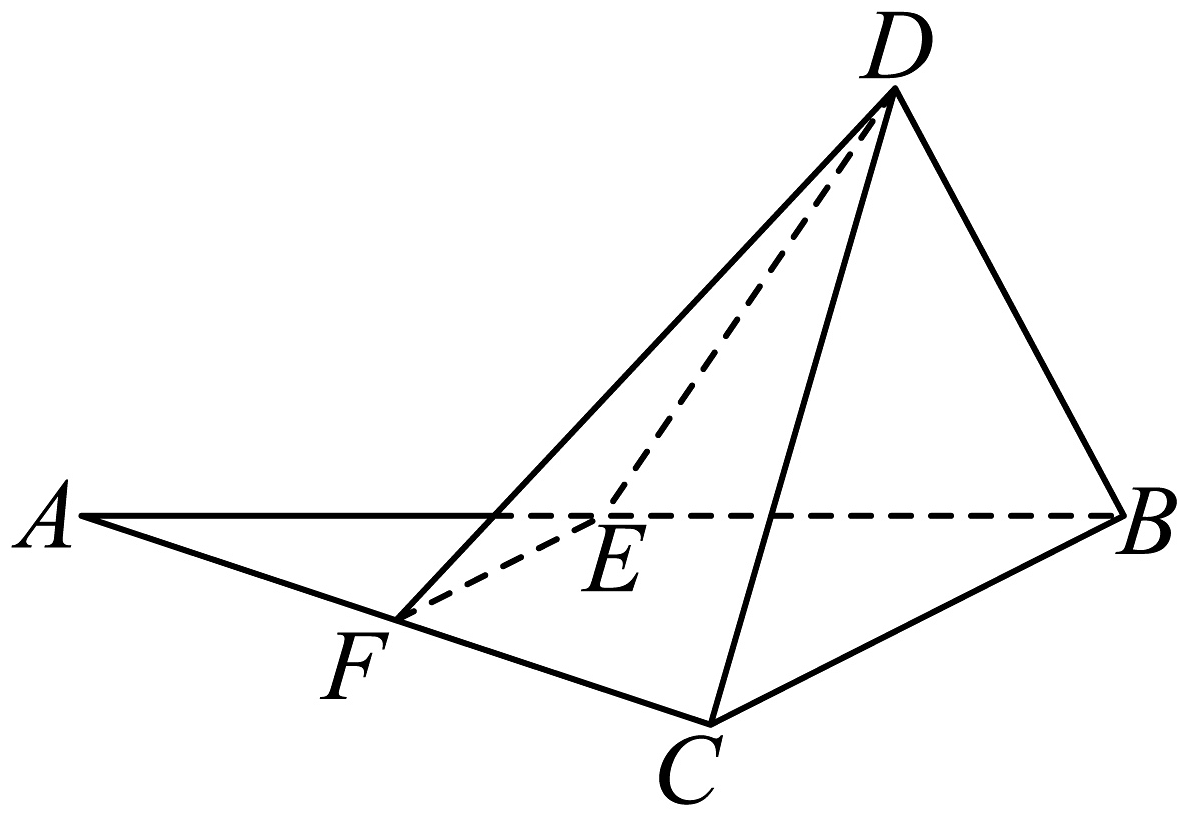 (1)、证明:平面(2)、若 , , 求平面与平面夹角的余弦值.
(1)、证明:平面(2)、若 , , 求平面与平面夹角的余弦值. -
17、已知等差数列的前项和为 . 且 . 则 .
-
18、已知椭圆的方程为 , 则( )A、椭圆关于轴对称 B、直线被椭圆截得弦长为 C、椭圆的长轴长为 D、椭圆的离心率为
-
19、已知函数 , 则下列结论正确的是( )A、的最小正周期为 B、的图象关于直线对称 C、不等式的解集为 D、若为的内角,且 , 则或
-
20、为了解某类植物生长年之后的高度.随机抽取了株此类植物.测得它们生长年之后的高度(单位:).将收集到的数据整理得到如下频率分布直方图.已知随机抽取的植物生长年之后高度低于的有株.根据此频率分布直方图.以下结论中正确的是( )
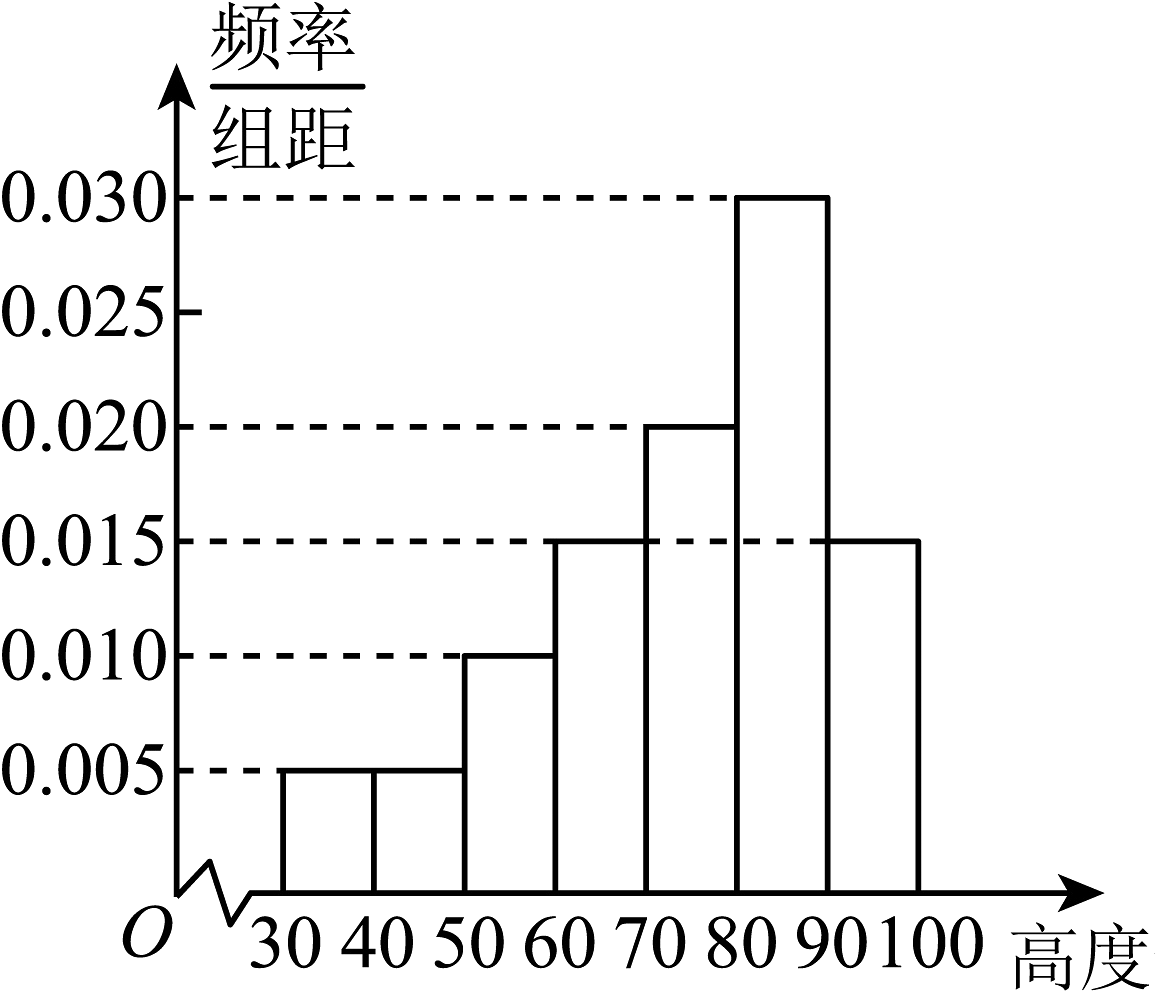 A、 B、此次检测植物生长高度在之间的有株 C、估计该类植物生长年后.高度的众数为 D、估计该类植物生长年后.高度的第百分位数为
A、 B、此次检测植物生长高度在之间的有株 C、估计该类植物生长年后.高度的众数为 D、估计该类植物生长年后.高度的第百分位数为