-
1、已知动点到点的距离比它到直线的距离小 , 记动点的轨迹为 .(1)、求轨迹的方程.(2)、直线与分别与轨迹交于点和点(与同向),且 , 线段与交于点 , 线段与的中点分别为 .
(ⅰ)求证:三点共线;
(ⅱ)若 , , 求四边形ABCD的面积.
-
2、如图,在圆柱中,四边形ABCD是其轴截面,EF为的直径, , , .
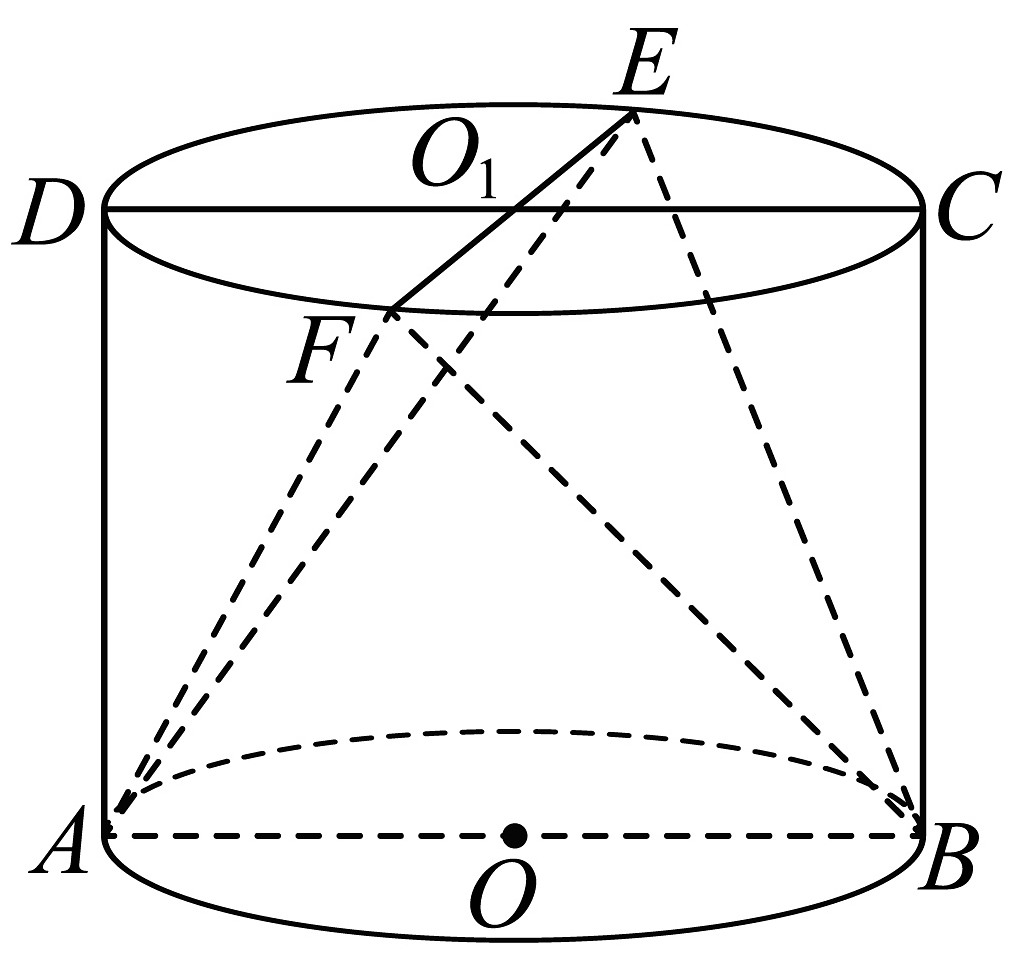 (1)、求证:;(2)、若四面体ABEF的体积为 , 求二面角平面角的余弦值.
(1)、求证:;(2)、若四面体ABEF的体积为 , 求二面角平面角的余弦值. -
3、为了切实加强学校体育工作,促进学生积极参加体育锻炼,养成良好的锻炼习惯,某高中学校计划优化课程,增加学生体育锻炼时间,提高体质健康水平,某体质监测中心抽取了该校10名学生进行体质测试,得到如下表格:
序号i
1
2
3
4
5
6
7
8
9
10
成绩(分)
38
41
44
51
54
56
58
64
74
80
记这10名学生体质测试成绩的平均分与方差分别为 , , 经计算 , .
(1)、规定体质测试成绩低于50分为不合格,从这10名学生中任取3名,记体质测试成绩不合格的人数为X,求X的分布列;(2)、经统计,高中生体质测试成绩近似服从正态分布 , 用 , 的值分别作为 , 的近似值,若监测中心计划从全省抽查10000名高中生进行体质测试,记这10000名高中生的体质测试成绩恰好落在区间的人数为Y,求Y的数学期望 .附:若 , 则 , , .
-
4、在中,内角A,B,C所对的边分别为a,b,c,已知 .(1)、求B;(2)、若 , 且满足 , 求的周长.
-
5、已知函数.若函数有七个不同的零点,则实数的取值范围是.
-
6、已知是椭圆的两个焦点,点M在C上,则的最大值为 .
-
7、设函数 , , 若是奇函数,则 .
-
8、已知四面体中, , , , 为四面体外接球的球心,则下列说法中正确的是( )A、若 , 则平面 B、若 , 则的取值范围是 C、若 , 则的取值范围是 D、若 , 直线与所成的角为 , 则四面体外接球的表面积为
-
9、随机事件A、B满足 , , , 下列说法正确的是( )A、事件与事件B相互独立 B、 C、 D、
-
10、设函数的定义域为 , 若 , 且对任意 , 满足: , , 则的值为( )A、 B、 C、 D、
-
11、已知数列满足的前12项组成一组数据,其第90百分位数为( )A、 B、 C、 D、
-
12、设F为双曲线( , )的右焦点, , 分别为C的两条渐近线的倾斜角,且满足 , 已知点F到其中一条渐近线的距离为 , 则双曲线C的焦距为( )A、 B、2 C、 D、4
-
13、已知平面向量 , 是两个单位向量,在上的投影向量为 , 则( )A、 B、1 C、0 D、
-
14、已知 , 函数的值域为 , 则实数的取值范围是( )A、 B、 C、 D、
-
15、已知集合 , 若 , 则实数( )A、1 B、 C、2 D、4
-
16、实数a,b满足 , 则( )A、 B、 C、1 D、3
-
17、已知点及圆 , 点是圆上的动点,则( )A、过原点与点的直线被圆截得的弦长为 B、过点作圆的切线,则切线方程为 C、当点到直线的距离最大时,过点与平行的一条直线的方程为 D、过点作圆的两条切线,切点分别为 , 则直线的方程为
-
18、已知正项数列的首项 , 前n项和满足.(1)、求数列的通项公式;(2)、记数列的前n项和为 , 若对任意的 , 不等式恒成立,求实数a的取值范围.
-
19、在①;②公差为 , 且成等比数列;③;三个条件中任选一个,补充在下面问题中,并给出解答.问题:已知数列是公差不为零的等差数列,其前项和为 , ______.(1)、求数列的通项公式;(2)、令 , 其中表示不超过的最大整数,求的值.
-
20、设数列的前项n和为 , 若对于任意的正整数n都有.
(1)设 , 求证:数列是等比数列,并求出的通项公式.
(2)求数列的前n项和.