-
1、在正方体中, , 点E,F,G分别为 , , 的中点,点在线段上运动(不包括端点),过G,P,的平面截正方体所得的截面周长的取值范围是.
-
2、若是曲线的切线,则.
-
3、除以8的余数为.
-
4、定义在上的非常数函数满足 , 且 , 则( )A、 B、是的一条对称轴 C、 D、
-
5、下列命题正确的是( )A、若事件A,B相互独立,则 B、若 , , , 则 C、已知随机变量 , 且 , 则 D、线性相关模型中,相关系数越大,两个变量的线性相关程度越强
-
6、已知实数 , , 且 , 则( )A、 B、 C、 D、
-
7、某平面四边形中, , , , 设 , .当的面积取得最大值时,的值为( )A、 B、 C、 D、
-
8、如图所示的九宫格中共有个格点,若在其中任取3个格点,恰好能构成三角形的取法共有( )种.
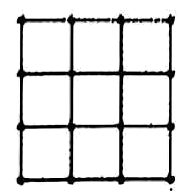 A、528 B、524 C、520 D、516
A、528 B、524 C、520 D、516 -
9、已知实数 , 正方形满足轴,且分别在 , , 的图象上,若正方形的面积为36,则( )A、 B、 C、 D、
-
10、已知向量是平面内的一组基底,则“ , 的夹角为锐角”是“”成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
11、已知 , 则( )A、 B、 C、 D、
-
12、如图,等腰梯形为某圆台的轴截面,满足 , 则该圆台的体积为( )
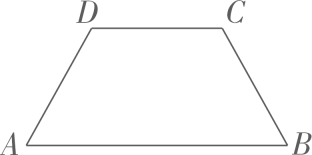 A、 B、 C、 D、
A、 B、 C、 D、 -
13、已知集合 , , 则中元素的个数为( )A、0 B、1 C、2 D、3
-
14、已知为虚数单位,( )A、 B、 C、 D、
-
15、已知复数(为虚数单位),则的虚部为( )A、 B、 C、 D、
-
16、已知点是圆上的动点,则点到直线距离的最小值是( )A、4 B、3 C、2 D、1
-
17、对于函数 , , 若存在非零常数和 , 使得对任意实数都有 , 且等式恒成立,则称函数是“类对称函数”.(1)、判断函数是否是“类对称函数”,请说明理由;(2)、设 , 若函数是“类对称函数”,求的值;(3)、设 , 证明:函数是“类对称函数”的充要条件是“且”.
-
18、如图,四边形为菱形,平面 , 过的平面交平面于 , .
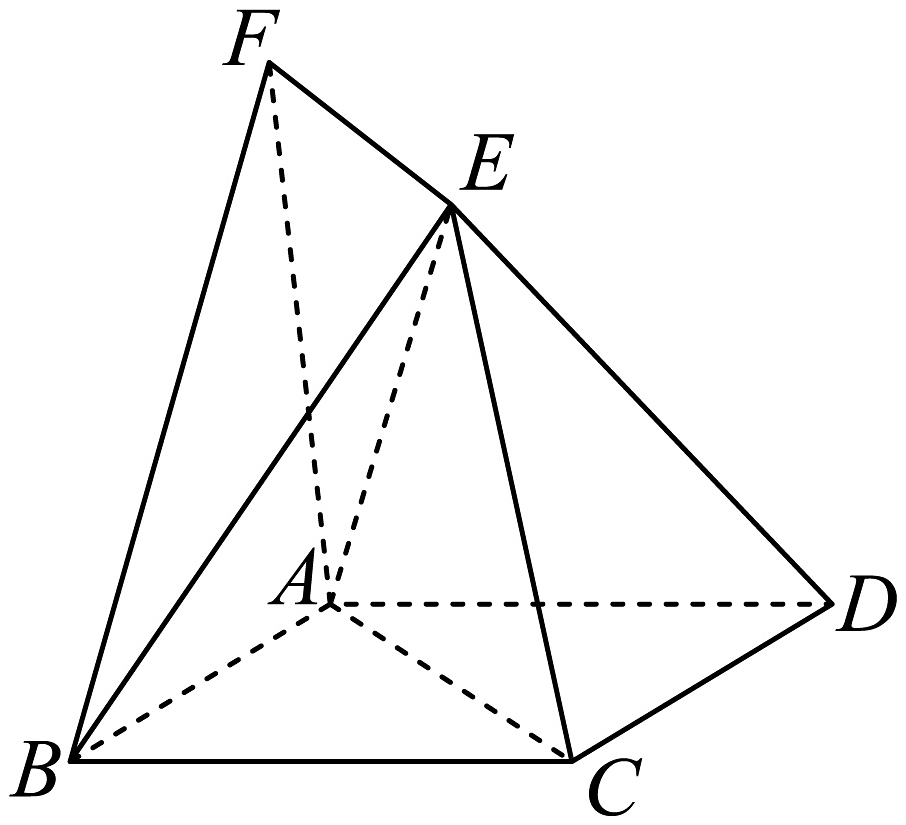 (1)、求证:平面;(2)、若平面平面 , , 且四棱锥的体积是 .
(1)、求证:平面;(2)、若平面平面 , , 且四棱锥的体积是 .①求的长;
②求直线与平面所成角的正弦值.
-
19、设函数 , 其中.(1)、若的最小正周期为 , 求的单调增区间;(2)、若函数图象在上存在对称轴,求的取值范围.
-
20、在中,角所对的边分别为 , 设向量 , 记 .(1)、求函数的最大值;(2)、若 , 求c.