-
1、已知是边长为1的正三角形,为中点,且 , 则( )A、 B、 C、 D、
-
2、下列说法不正确的是( )A、对具有线性相关关系的变量 , , 且回归方程为 , 若样本点的中心为 , 则实数的值是 B、若随机变量服从正态分布 , 且 , 则 C、若线性相关系数越接近1,则两个变量的线性相关程度越高 D、一组数据10,10,11,12,12,14,16,19,21,21的第80百分位数为19
-
3、已知函数 , 曲线在点处的切线与直线平行,则实数的值为( )A、 B、 C、 D、1
-
4、设等差数列的前项和为 , 若 , , 则( )A、20 B、18 C、16 D、15
-
5、已知函数.
(1)讨论的单调性;
(2)若 , 且函数只有一个零点,求的最小值.
-
6、在中,点的坐标为 , 边上的中线所在直线的方程为 , 直线的倾斜角为 .(1)、求点的坐标;(2)、过点的直线与轴的正半轴、轴的正半轴分别交于 , 两点,求(为坐标原点)面积的最小值.
-
7、已知函数( , 且)的部分图象如图示.
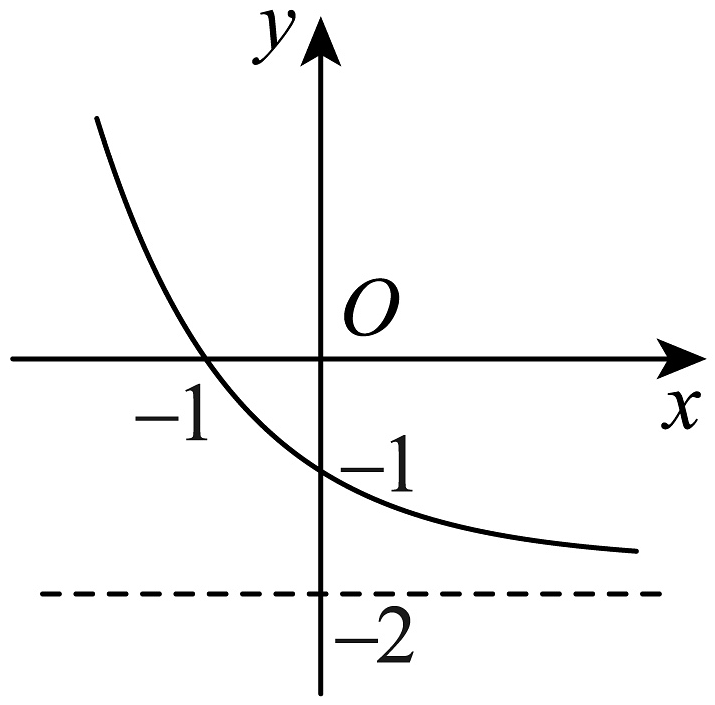 (1)、求的解析式;(2)、若关于x的不等式在上有解,求实数m的取值范围.
(1)、求的解析式;(2)、若关于x的不等式在上有解,求实数m的取值范围. -
8、在《九章算术》中,将底面为矩形且有一条侧棱与底面垂直的四棱锥称之为阳马.如图,若四棱锥为阳马,侧棱底面 , 且 , , 设该阳马的外接球半径为 , 内切球半径为 , 则 .
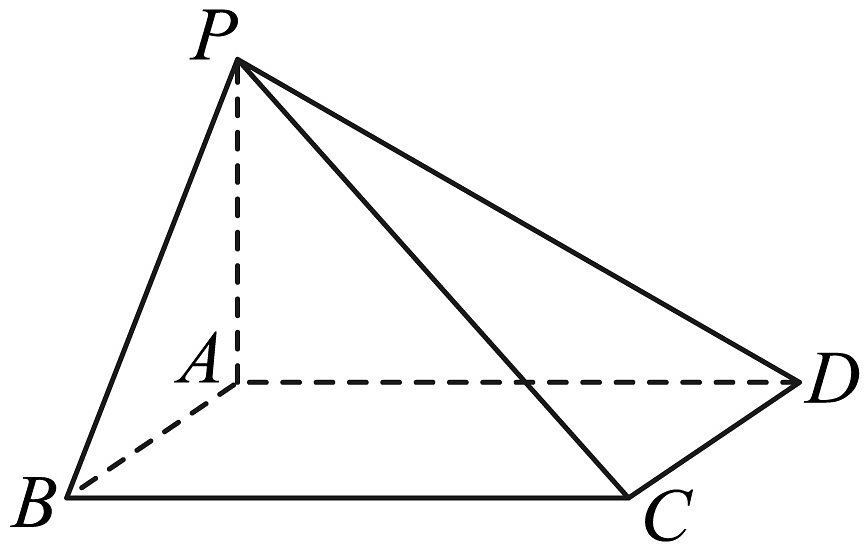
-
9、若函数的零点在区间 , 内,则 .
-
10、已知集合 , 则( )A、 B、 C、 D、
-
11、甲、乙、丙、丁、戊5名学生站成一排,记“甲、乙相邻”为事件 , “甲不站在两端”为事件 , 则( )A、 B、 C、 D、
-
12、已知椭圆(且)的焦点为为上的一点,若的周长为18,则椭圆的离心率为 .
-
13、设 , 对任意 , 成立,则该函数称为“级函数”,其中为函数的导数.(1)、判断函数和 , 是否为“级函数”,并说明理由;(2)、记(1)中的“级函数”为 .
①若 , , 使得 , 证明:;
②若 , , 求实数的取值范围.
-
14、某旅游景点统计今年五一期间进入景区的游客人数(单位:千人)如下:
日期
5月1日
5月2日
5月3日
5月4日
5月5日
第天
1
2
3
4
5
参观人数
2.2
2.6
3.1
5.2
6.9
(1)、根据上表数据,判断成对样本数据的线性相关程度,请用样本相关系数加以说明;(若 , 则认为与的线性相关性很强),如果与的线性相关性很强,那么求出关于的经验回归方程;(2)、五一期间景区开放南门、东门和北门供游客出入,游客从南门、东门和北门进入景区的概率分别为 , 且出景区与入景区选择相同门的概率为 , 选择与入景区不同两门的概率各为 . 假设游客从南门、东门、北门出入景点互不影响,现有甲、乙、丙、丁4名游客于5月1日游玩景点,设为4人中从东门出景区的人数,求的分布列、期望及方差.附:参考数据: , , , , .
参考公式:经验回归方程 , 其中 , .
样本相关系数 .
-
15、函数的定义域为 , 如果 , 都有恒成立,那么的图象关于对称.已知 .(1)、讨论的单调性;(2)、当时,
①证明:函数图象关于对称;
②求的值.
-
16、为调查学生喜欢在食堂就餐是否和性别有关,学校随机调研了男女生各100人,经统计得到如下列联表:
男
女
喜欢
80
40
不喜欢
20
60
(1)、依据的独立性检验,判断学生喜欢在食堂就餐是否与性别有关?(2)、为听取学生对食堂的建议,从学生中抽取9人召开座谈会,并给其中3名同学赠送礼品,每人1份(其余人员仅赠送餐券).已知参加座谈会的学生中有且只有4名学生来自高一,求高一这4名学生中得到礼品的人数的分布列和数学期望.0.010
0.005
0.001
6.635
7.879
10.828
附: , 其中
-
17、如图,四棱锥的底面是矩形,平面 , , 为的中点.
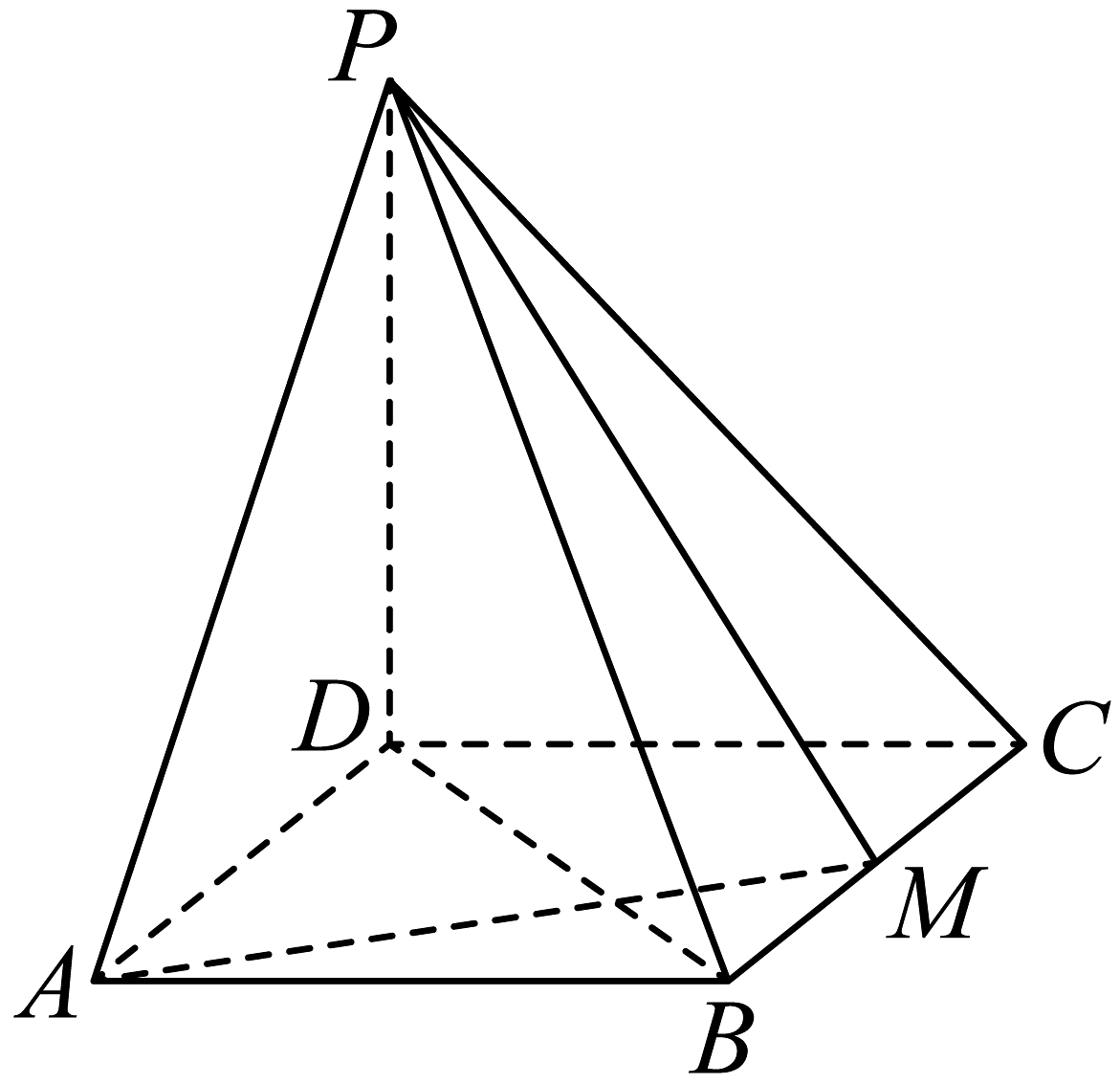 (1)、求证:平面;(2)、求平面与平面夹角的余弦值.
(1)、求证:平面;(2)、求平面与平面夹角的余弦值. -
18、已知 , , 且 . 则满足条件的集合共有个.
-
19、的展开式的常数项是 .
-
20、已知 , 且 , 则 .