-
1、已知函数 .(1)、求在点处的切线方程;(2)、求函数的极值;(3)、判断方程的解的个数.
-
2、定义:平面点集中的每一点都有唯一的实数与之对应,则称为上的二元函数.若点的横、纵坐标均为整数,则称点为“整数点”.已知 , 则方程的“整数点”为 .
-
3、从甲、乙、丙3人中选2人参加两项活动,有种不同的选法.
-
4、如图,已知笛卡尔“鸡蛋”曲线过点 , 且曲线上任意一点到和的距离满足 , 则( )
 A、 B、曲线与单位圆有3个交点 C、的最小值为 D、的最大值为
A、 B、曲线与单位圆有3个交点 C、的最小值为 D、的最大值为 -
5、已知函数 , 下列选项正确的有( )A、若 , 则函数为奇函数 B、若有极小值0,则 C、若有极大值2,则 D、可能在处有极大值
-
6、设样本数据 , 若 , 则( )A、的平均数等于的平均数 B、的中位数小于的中位数 C、的极差大于的极差 D、的方差小于的方差
-
7、已知函数的定义域为 , 满足 . 当时, , 则的最大值是( )A、6 B、3 C、5 D、8
-
8、若 , 则( )A、 B、 C、 D、
-
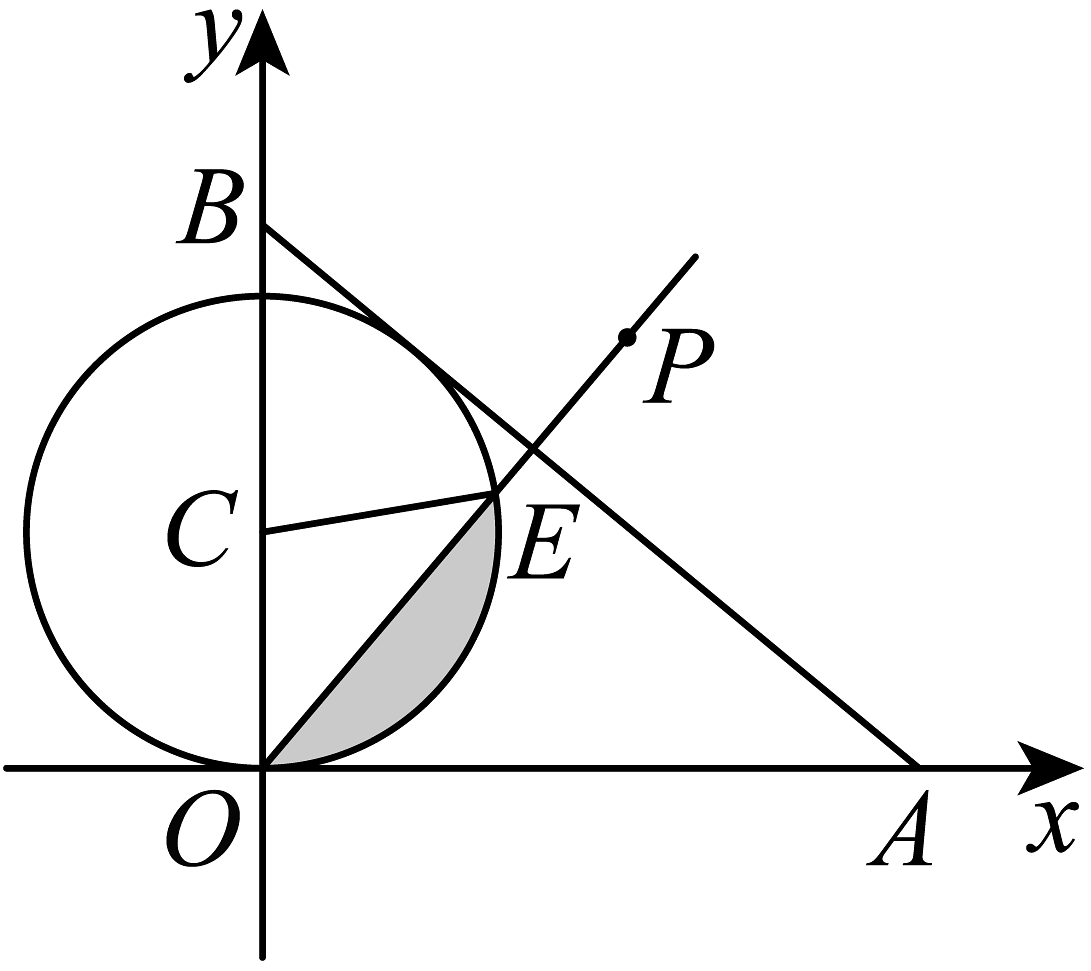
9、如图,圆C和的两条边相切,射线OP绕点O从OA开始逆时针方向旋转至OB,设 , 在旋转过程中,OP扫过的圆内阴影部分的面积为S,则S关于θ的图象可能是( )
 A、
A、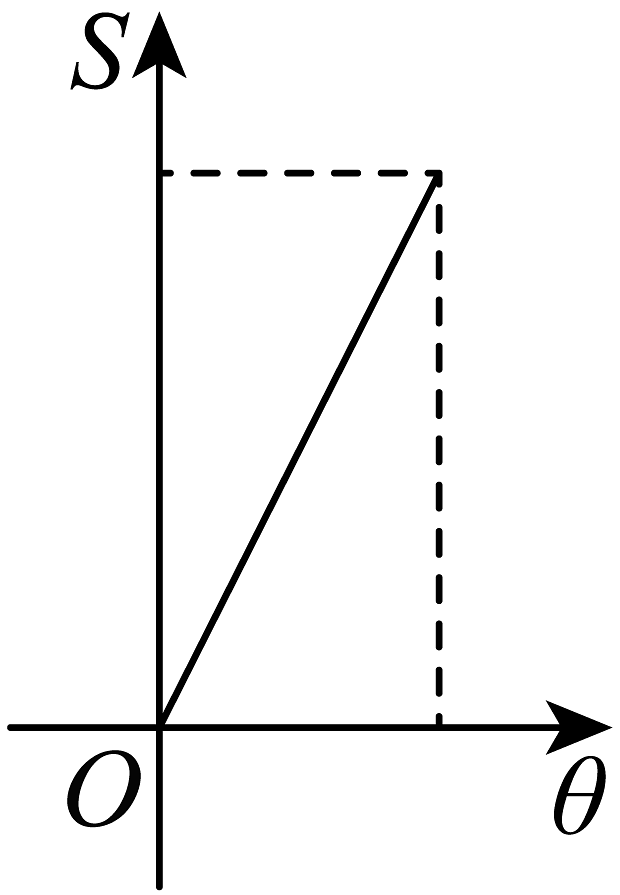 B、
B、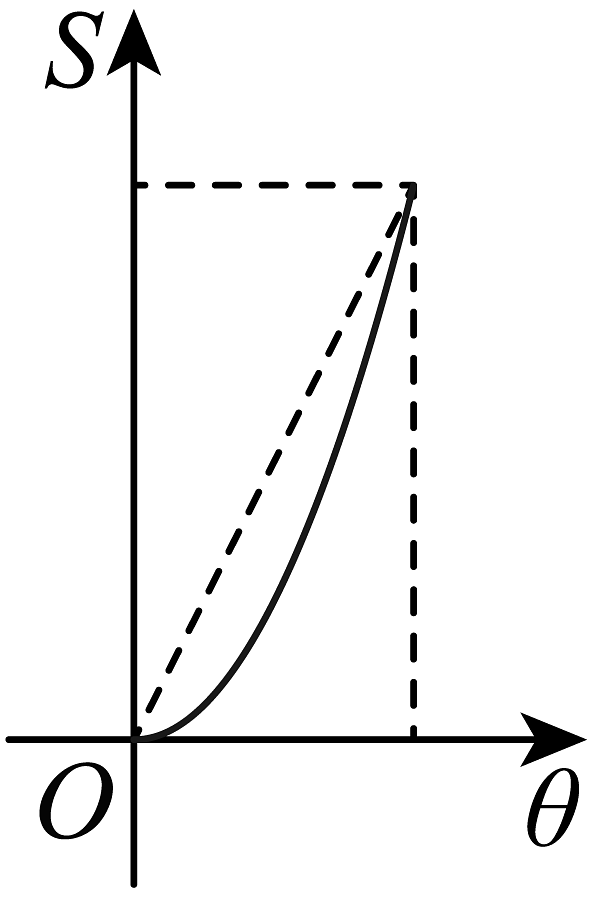 C、
C、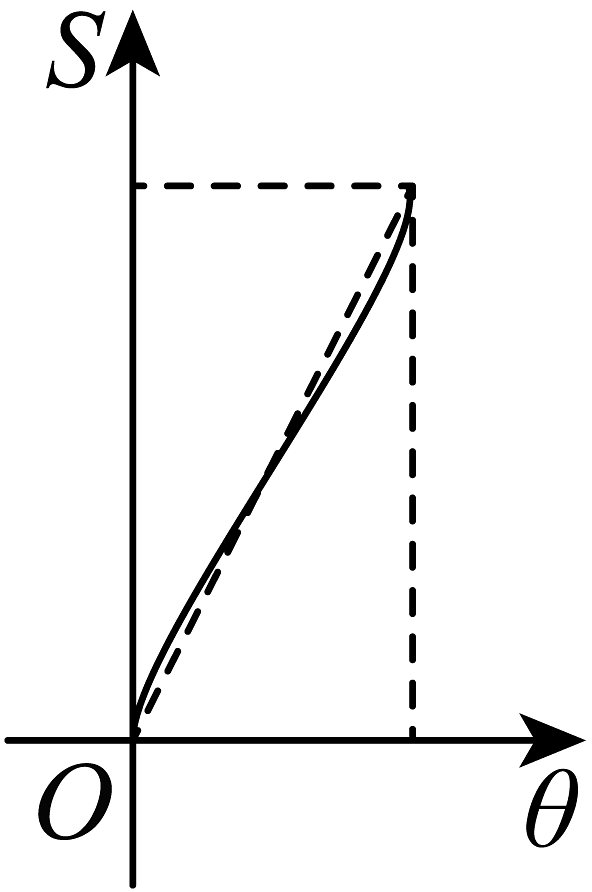 D、
D、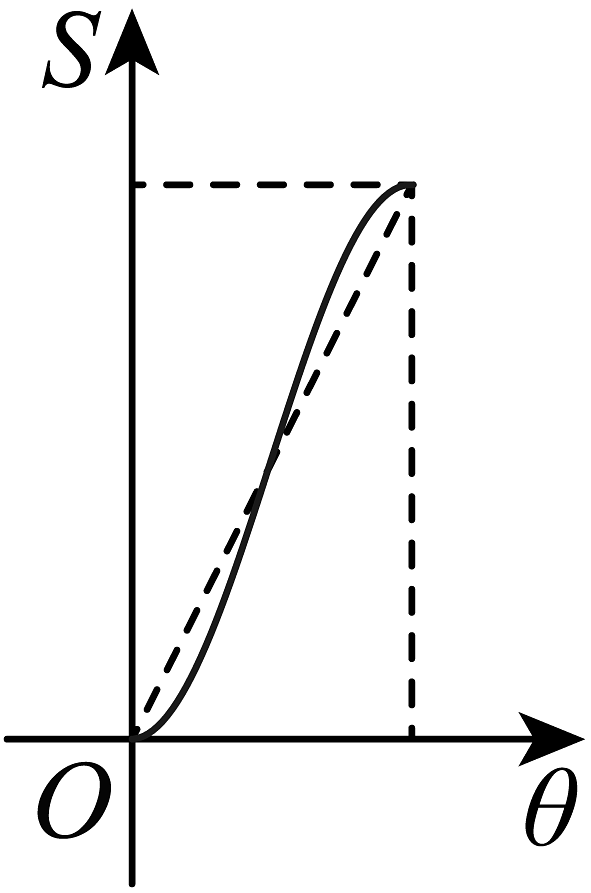
-
10、若随机变量服从正态分布 , 则( )A、 B、 C、 D、
-
11、的展开式中第4项的系数是( )A、20 B、15 C、160 D、120
-
12、若是两条直线,是两个平面,且 . 设 , 则是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
13、设数列的前项和为 . 若 , 则( )A、1 B、 C、2 D、
-
14、已知集合 , 则( )A、 B、 C、 D、
-
15、已知双曲线的左、右顶点分别是 , , 点在双曲线上,且直线 , 的斜率之积为1.(1)、求双曲线的标准方程;(2)、已知 , 分别是双曲线的左、右焦点,点G是圆上的动点,若K是双曲线左支上一动点,求的最小值;(3)、已知两平行直线和 , 直线过点交双曲线的右支于A,B两点,直线过点交双曲线的右支于C,D两点,记AB,CD的中点分别为P,Q,过点Q作双曲线的两条渐近线的垂线,垂足分别为M,N.求四边形PMQN面积的取值范围.
-
16、已知非零等差数列的前n项和为 , 且 , .(1)、求的通项公式;(2)、已知正项数列满足: , 且是和的等差中项,求数列的前n项和;(3)、在条件(2)下,记正项数列的前n项和为 . 求证: .
-
17、已知函数 , .(1)、若函数在上单调递增,求实数a的取值范围;(2)、若为函数的极值点,求a的值;(3)、设函数 , 当时,若对于任意 , 总存在 , 使得 , 求实数b的取值范围.
-
18、如图,在长方体中, , 点E是棱的中点.
 (1)、求证:平面BDE;(2)、求直线与平面BDE所成角的正弦值.
(1)、求证:平面BDE;(2)、求直线与平面BDE所成角的正弦值. -
19、中国的非遗项目丰富多样,涵盖广泛,体现了中华民族的智慧和独特的文化魅力.春节期间某地为充分宣扬该地非遗物质文化,加大非遗传承人的技艺展示.该地市场开发与发展机构统计了非遗传承人的技艺展示量与市场消费收入的6组数据如下表:
技艺展示量x(单位:个)
21
23
24
27
29
32
市场消费收入y(单位:万元)
6
11
20
27
57
77
(1)、若用线性回归理论进行统计分析,求市场消费收入y关于技艺展示量x的回归方程(精确到0.1);(2)、若用非线性回归模型求得市场消费收入y关于技艺展示量x的回归方程为 , 且决定系数 , 与(1)中的线性回归模型相比,应用决定系数说明哪种模型的拟合效果更好.附:一组数据 , , …, , 其回归直线的斜率和截距的最小二乘估计为 , ;决定系数
参考数据: , , ,
线性回归模型的残差平方和为(其中 , 分别为非遗传承人的技艺展示量和市场消费收入,).
-
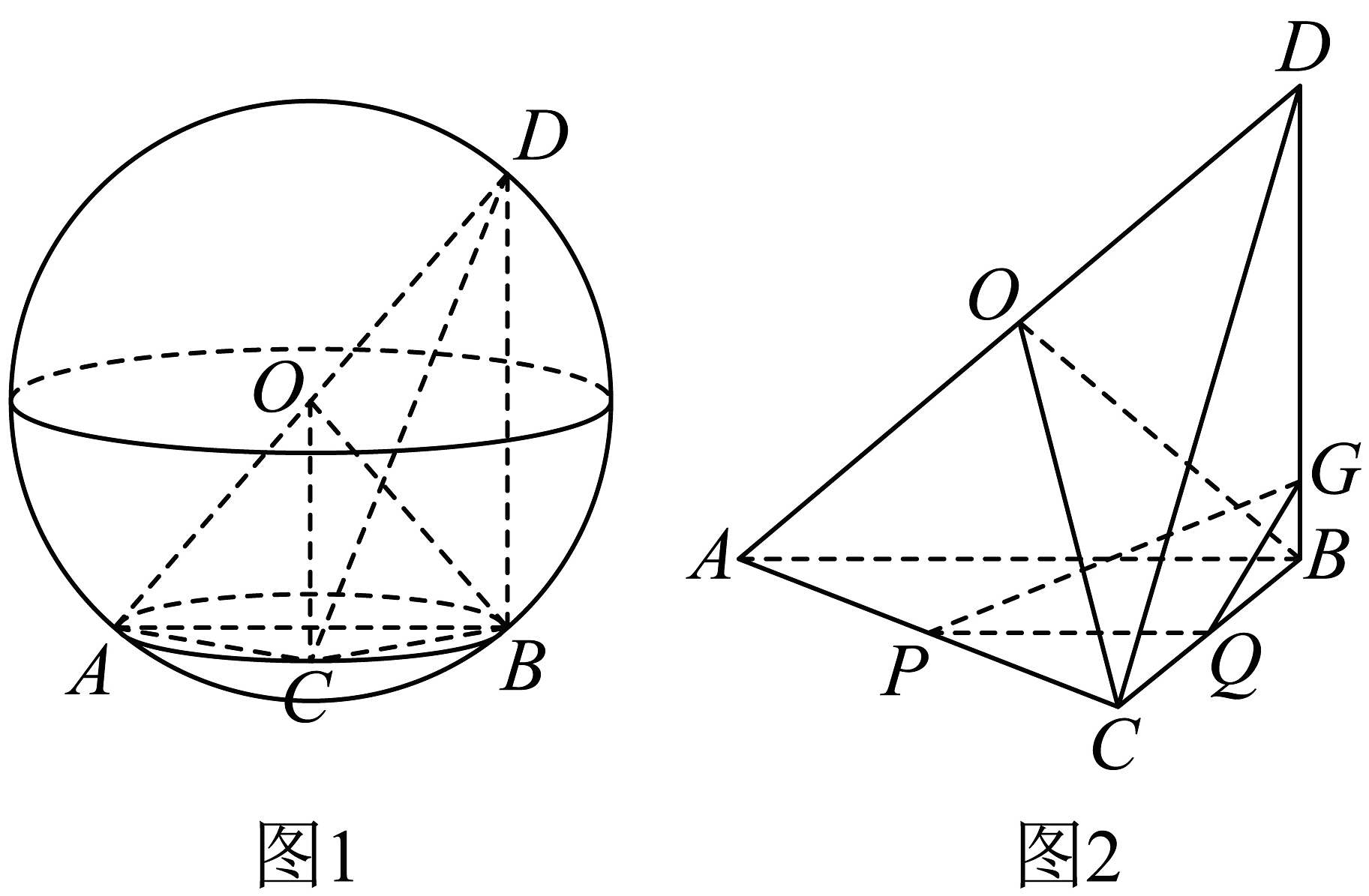
20、如图1,已知球O的半径 . 在球O的内接三棱锥中.平面 , , , . P,Q分别为线段AC,BC的中点,G为线段BD上一点(不与点B重合),如图2.则平面与平面夹角的余弦值的最大值为 .