-
1、已知数列的前项和为 , 且.(1)、求数列通项公式;(2)、数列满足 , 求数列的前项和;(3)、设 , 求证:数列中任意不同的三项都不能构成等差数列.
-
2、已知函数 , 函数 .(1)、求的最小值;(2)、若 .
①求零点的个数;
②证明:的所有零点之和为定值.
-
3、以“‘智’在必得”为主题的人工智能知识挑战赛预赛由6道正误判断题组成,每位选手从中随机抽取3道,若能全部回答正确,则通过预赛.已知选手甲会做其中的4道题.(1)、设表示选手甲抽到会做题目的道数,求随机变量的分布列和方差;(2)、假设选手甲会做的题全部答对;不会做的题随机判断,答对的概率为.若各题作答结果互不影响,求他通过预赛的概率.
-
4、为了了解高中学生课后自主学习数学时间(x分钟/每天)和他们的数学成绩(y分)的关系,某实验小组做了调查,得到一些数据如下表:
编号
1
2
3
4
5
x
10
20
30
40
50
y
70
80
100
120
130
(1)、若该组数据中y与x之间的关系可用线性回归模型进行拟合,求y关于x的回归直线方程.(参考数据:)(2)、基于上述调查,某校提倡学生课后自主学习.经过一学期的实施后,抽样调查了160位学生.按照参与课后自主学习与成绩进步情况得到如下2×2列联表:成绩没有进步
成绩有进步
合计
参与课后自主学习
5
135
140
未参与课后自主学习
5
15
20
合计
10
150
160
依据的独立性检验,分析“课后自主学习与成绩进步”是否有关.
附:回归方程中斜率和截距的最小二乘估计公式分别为: ,
, 其中 .
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
-
5、在中,若 , 则的最大值为.
-
6、甲、乙、丙、丁、戊五人完成A,B,C,D,E五项任务所获得的效益如下表:现每项任务选派一人完成,其中甲不承担C任务,丁不承担A任务的指派方法数有种;效益之和的最大值是.
A
B
C
D
E
甲
11
13
10
13
11
乙
25
26
24
23
23
丙
10
14
15
13
11
丁
7
9
11
9
11
戊
14
16
15
16
12
-
7、已知随机变量 , 则.
-
8、已知函数在处取得极小值,则下列结论正确的是( )A、或 B、函数有且仅有一个零点 C、函数恰有两个极值点 D、函数在有最小值,无最大值
-
9、已知等比数列 , , , 则( )A、数列是等比数列 B、数列的前和是 C、数列是等差数列 D、数列的前10项和是
-
10、已知等差数列的前项和为 , 且 , 则( )A、52 B、96 C、106 D、12
-
11、“”是“函数只有一个零点”的( )A、充要条件 B、必要不充分条件 C、充分不必要条件 D、既不充分也不必要条件
-
12、以下四个命题中,其中真命题为( )A、在回归分析中,可用相关指数的值判断模型的拟合效果,越大,模型的拟合效果越好; B、两个随机变量的线性相关性越强,相关系数的越大; C、若数据 , , …,的方差为1,则 , , …,的方差为; D、对分类变量与的随机变量的观测值来说,越小,判断“与有关系”的把握程度越大.
-
13、在等差数列中,若 , , 则公差( )A、 B、 C、 D、
-
14、已知函数 , 则( )A、 B、2 C、 D、
-
15、若随机变量 , 且 , 则( )A、0.4 B、0.5 C、0.6 D、0.7
-
16、函数的定义域为;
①若对 , 都有成立,则称在上为凹函数(当且仅当时,等号成立),且凹函数有以下性质:对都有(当且仅当时,等号成立).
②若对 , 都有成立,则称在上为凸函数(当且仅当时,等号成立),且凸函数有以下性质:对都有(当且仅当时,等号成立).
(1)、判断函数在上是否具有凹凸性,并用上述定义法证明你的结论.(2)、设为的周长,为的面积;(i)求:的取值范围;
(ii)证明:.
-
17、2025年,某卫视推出了“最强大脑围棋版争霸赛”,堪称围棋界史上最激烈的国际赛事,以“棋艺封神,一站扬名”为口号,致力于推广围棋文化和智力竞技.受此启发,某中学为了让学生亲身体验围棋比赛的精彩和激烈,激发学生的思维活力,特别举办了“校园棋王争霸赛”.根据已报名的学生资料统计,有的学生学过围棋,将频率视为概率.(1)、从已报名选手中任取3名学生,记其中学过围棋的学生数为 , 求的分布列与数学期望;(2)、经过海选,最终决定、、、、、、、八位棋手参加棋王争霸赛,比赛分预赛、半决赛和决赛三个阶段,采用淘汰制决出冠军.预赛共有四场,八位棋手赛前抽签确定比赛位置,获胜的四人进入半决赛,依次类推,在决赛中,胜者为冠军,负者为亚军。已知~这7位棋手互相对弈时,获胜概率均为 , 棋手与其他棋手对弈时,获胜的概率为 , 每局对弈结果相互独立,无和棋情况.
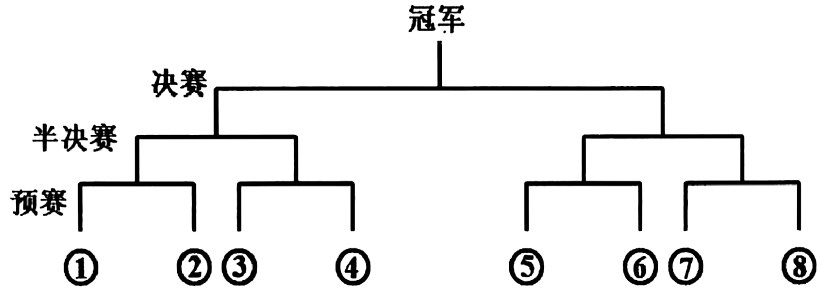
(ⅰ)求棋手最终夺冠的概率;
(ⅱ)求棋手与有过对弈且最终获得亚军的概率.
-
18、如图,已知四棱台 , 点在底面上的射影落在线段上(不含端点),底面为直角梯形, , , , .
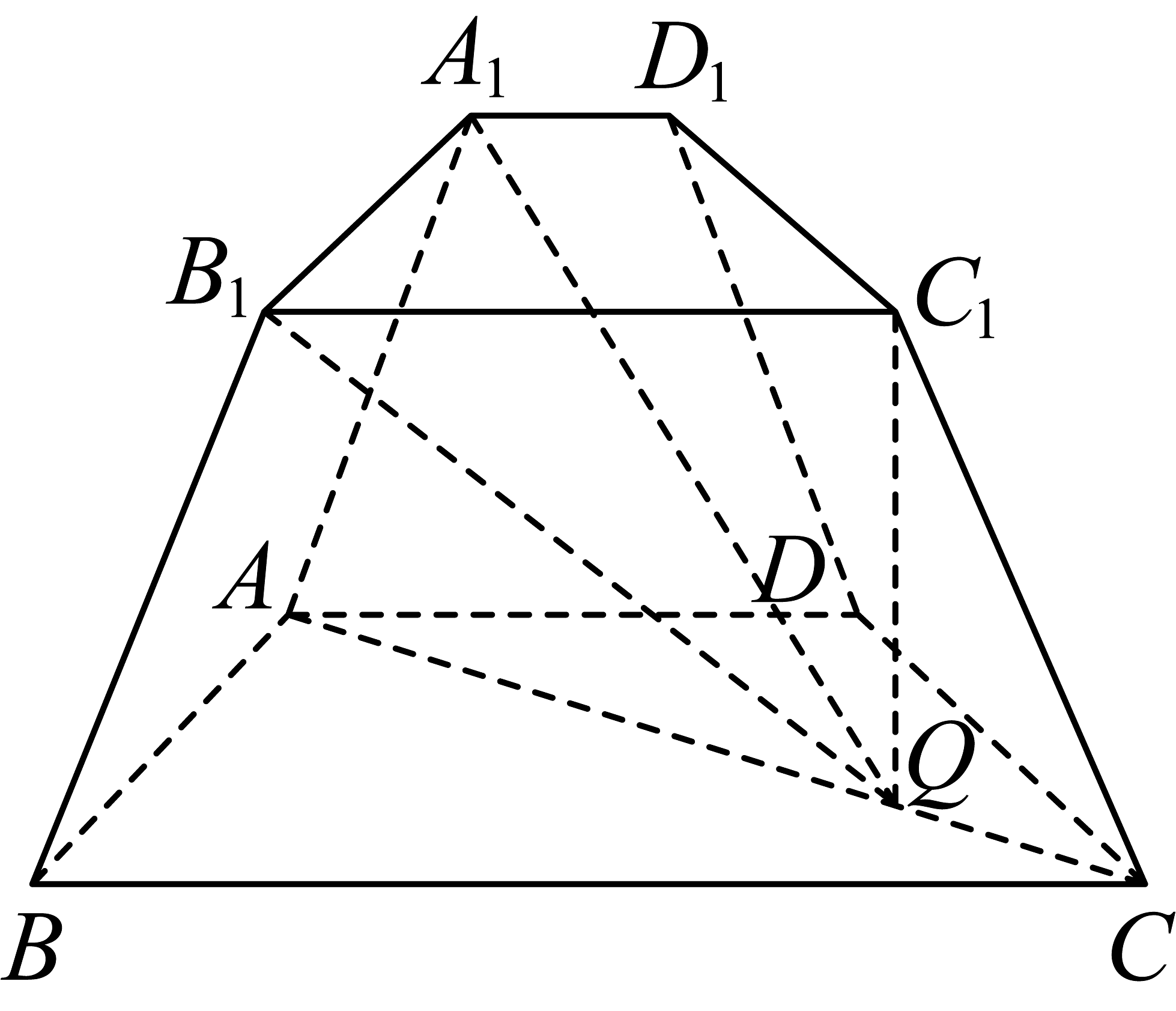 (1)、求证:平面;(2)、若二面角的大小为;
(1)、求证:平面;(2)、若二面角的大小为;(ⅰ)求直线与平面所成的角;
(ⅱ)若四边形为等腰梯形, , 求平面与平面夹角的正切值.
-
19、已知平面向量、满足 , , .(1)、求在上的投影向量(结果用表示);(2)、求;(3)、若 , 求.
-
20、在中,、、分别为的内角、、的对边,满足 , 为的中点.(1)、求角的大小;(2)、若 , , 求线段的长度.