-
1、已知在△ABC中,a,b,c分别为∠A,∠B,∠C的对边,且a=4,b+c=5,tanB+tanC+=tanBtanC,则△ABC的面积为 ( )A、 B、3 C、 D、
-
2、如图,A,B两地相距45km,甲欲驾车从A地去B地,由于山体滑坡造成道路AB堵塞,甲沿着与AB方向成18°角的方向前行,中途到达C点,再沿与AC方向成153°角的方向继续前行到达终点B,则这样的驾车路程比原来的路程约多了( )(参考数据: , , )
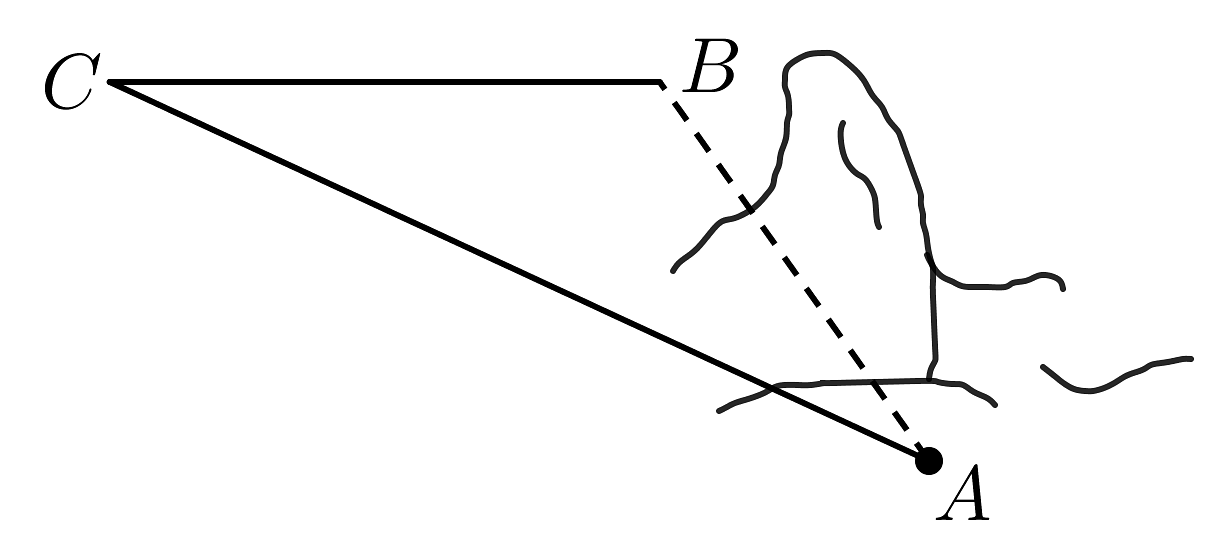 A、45.5km B、51.5km C、56.5km D、60.5km
A、45.5km B、51.5km C、56.5km D、60.5km -
3、已知某中学共有学生1000名,其中男生有600人,现按性别采用分层随机抽样的方法抽取100人,抽取的样本中男生身高的平均数和方差分别为160和4,女生身高的平均数和方差分别为155和3,则估计该校学生身高的总体方差是( )A、9.6 B、9 C、8.6 D、8
-
4、圆锥的底面圆半径 , 侧面的平面展开图的面积为 , 则此圆锥的体积为( )A、 B、 C、 D、
-
5、已知是在上单调递增的奇函数,则函数在上的图象可能为( )A、
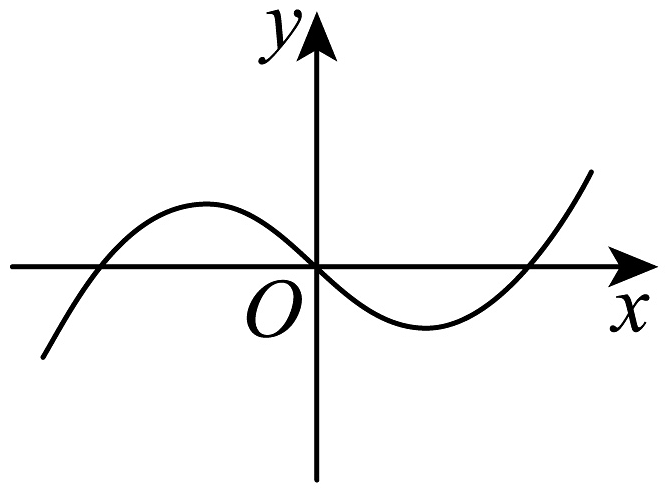 B、
B、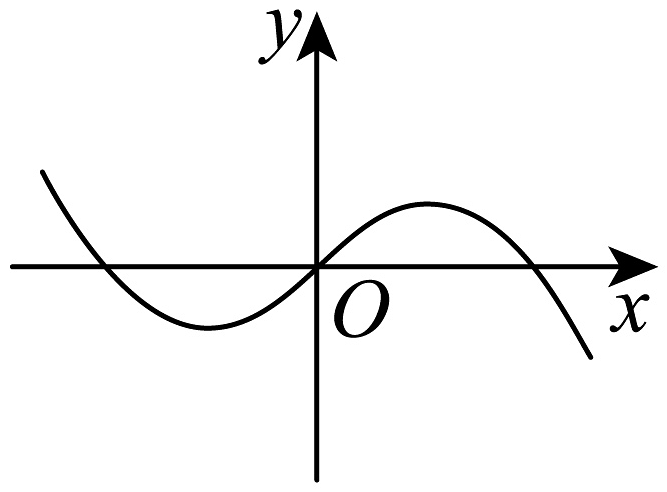 C、
C、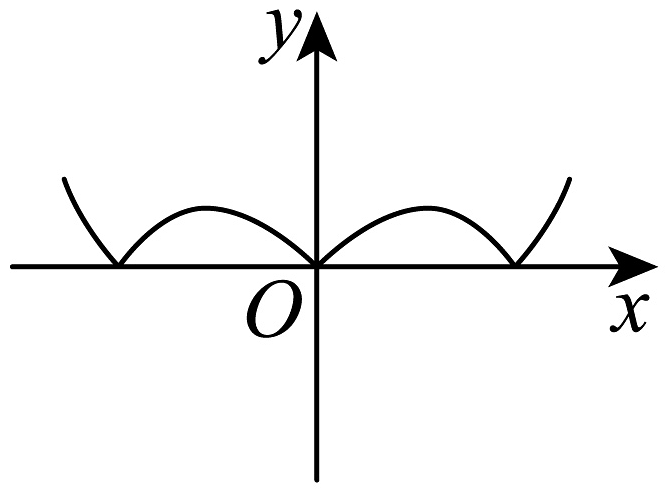 D、
D、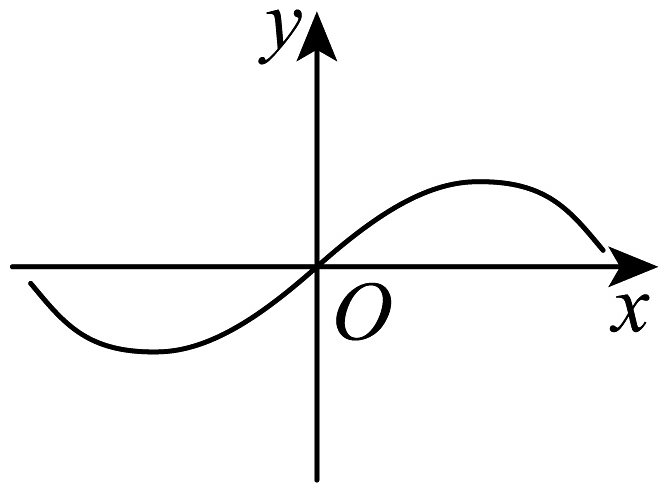
-
6、若平面向量两两的夹角相等,且 , , , 则( )A、1 B、4 C、1或4 D、1或2
-
7、已知复数满足 , 则( )A、 B、1 C、 D、2
-
8、已知函数 , 其中常数.(1)、若在上是增函数,求实数的取值范围;(2)、若 , 设 , 求证:函数在上有两个极值点.
-
9、已知过点的双曲线的渐近线方程为.如图所示,过双曲线的右焦点作与坐标轴都不垂直的直线交的右支于两点.
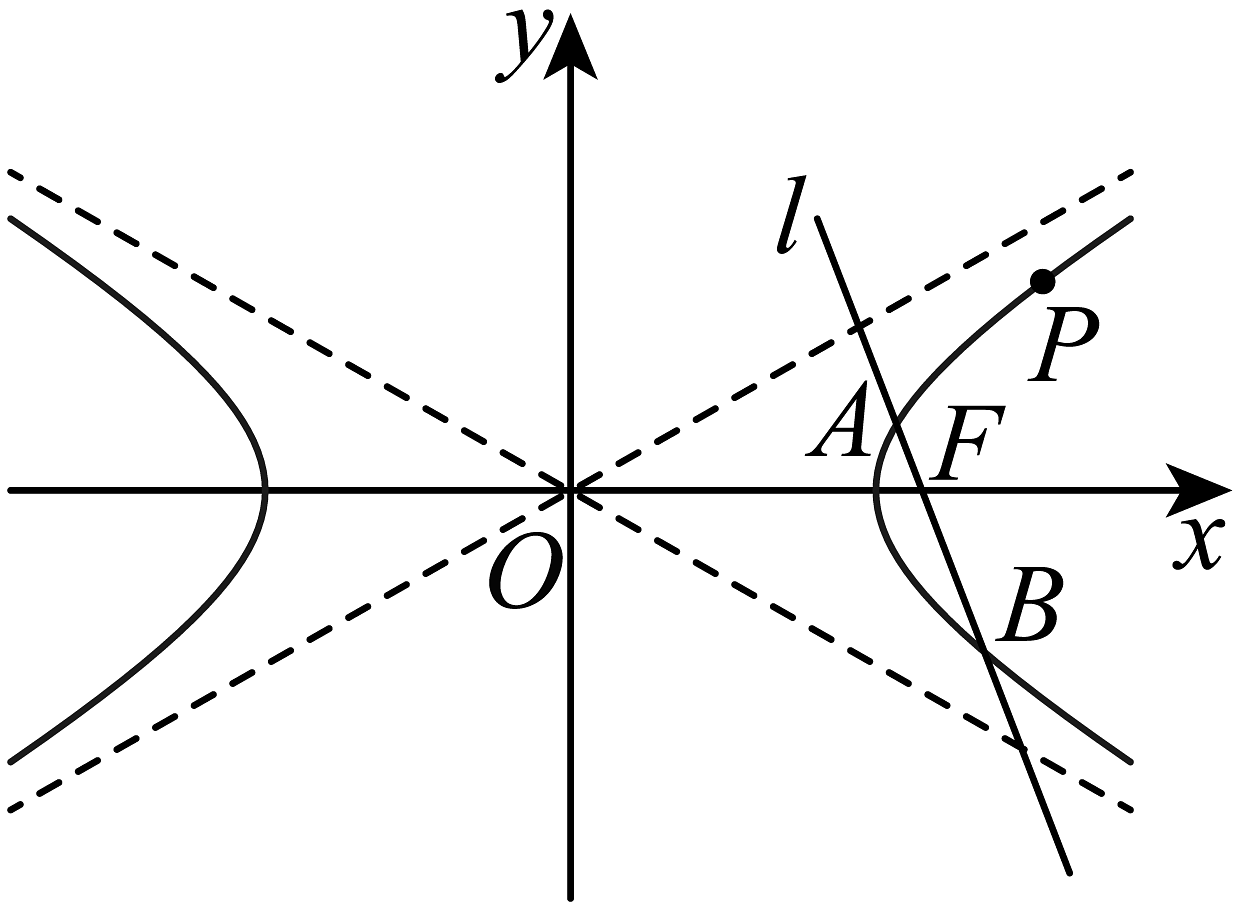 (1)、求双曲线的标准方程;(2)、若双曲线上的点到其两条渐近线的距离分别为 , 求的值;(3)、已知点 , 求证:.
(1)、求双曲线的标准方程;(2)、若双曲线上的点到其两条渐近线的距离分别为 , 求的值;(3)、已知点 , 求证:. -
10、如图,在四棱锥上,底面为直角梯形, , , 平面平面 , 为的中点,是棱上的点, , , .
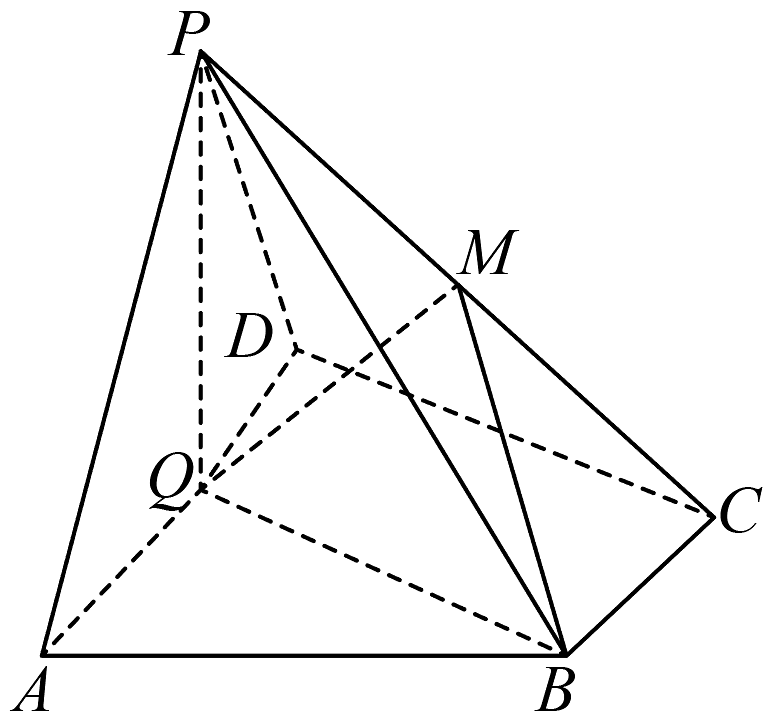 (1)、求证: 平面平面(2)、若二面角大小为 , 求的值
(1)、求证: 平面平面(2)、若二面角大小为 , 求的值 -
11、中,内角的对边分别是 , 已知成等比数列,且 .
(I)求的值;
(II)设 , 求的值.
-
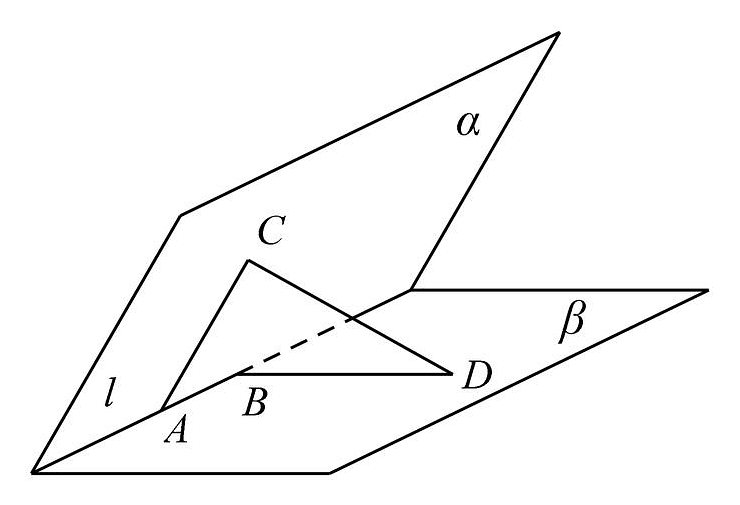
12、如图所示,二面角为 , 是棱上的两点,分别在半平面内 , 且 , , , , , 则的长 .
-
13、已知且 , 则.
-
14、已知在数列中, , , 其前项和为 , 则( )A、当时, B、当时,数列是递增数列 C、 D、对任意 , 存在 , 使得数列成等比数列
-
15、下列说法正确的有( )A、数据的第75百分位数是40 B、若 , 则 C、4名学生选报3门校本选修课,每人只能选其中一门,则总选法数为种 D、展开式中项的二项式系数为56
-
16、已知点是椭圆上的动点,过点作圆的切线,为其中一个切点,则的取值范围为A、 B、 C、 D、
-
17、已知 , 则( )A、 B、 C、 D、
-
18、在中, , 若 , 则的最大值是A、 B、 C、 D、
-
19、两枚骰子,设出现的点数之和分别为9,10,11的概率分别为p1 , p2 , p3 , 则( )A、p1<p2=p3 B、p1>p2>p3 C、p1=p2>p3 D、p1>p2=p3
-
20、已知非常数函数满足 , 则下列函数中,不是奇函数的为( )A、 B、 C、 D、