相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、记是内角 , , 的对边分别为 , , .已知 , 点在边上,.
(1)证明:;
(2)若 , 求.
-
2、已知等差数列的前项和 , 若 , 且四点共面(为该平面外一点),则 .
-
3、与圆柱底面成角的平面截圆柱得到如图所示的几何体,截面上的点到圆柱底面距离的最大值为4,最小值为2,则该几何体的体积为.

-
4、已知 , 函数 , 则( )A、的图像关于轴对称 B、恰有2个极值点 C、在上单调递增 D、的最小值小于
-
5、如图,若正方体的棱长为2,点是正方体在侧面上的一个动点(含边界),点是棱的中点,则下列结论正确的是( )
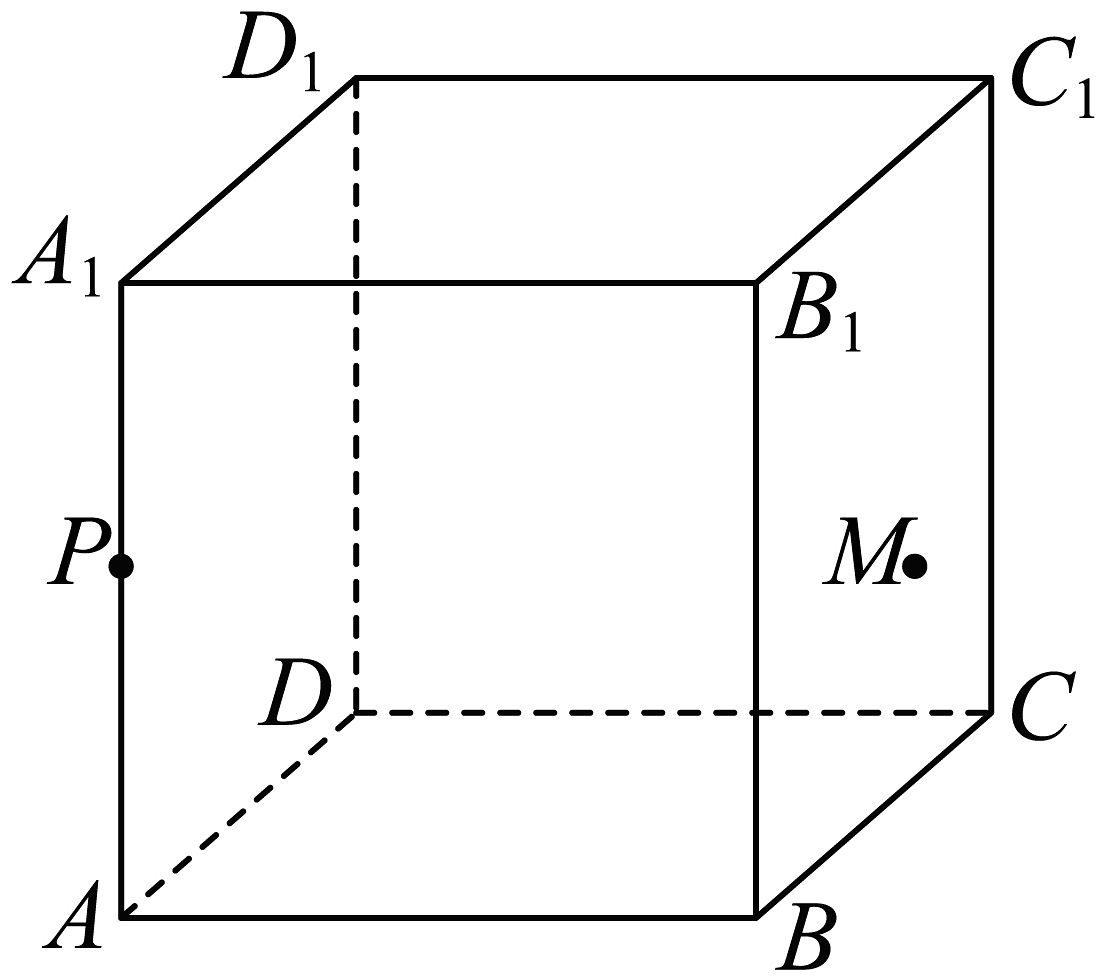 A、三棱锥的体积为 B、若 , 则点的轨迹是以为半径的半圆弧 C、若 , 则的最大值为3 D、若为的中点,则过三点的平面截三棱锥的截面面积为
A、三棱锥的体积为 B、若 , 则点的轨迹是以为半径的半圆弧 C、若 , 则的最大值为3 D、若为的中点,则过三点的平面截三棱锥的截面面积为 -
6、已知等差数列中, 记 , , 则数列的前项和为( )A、 B、 C、 D、
-
7、阅读材料:空间直角坐标系中,过点且一个法向量为的平面的方程为 . 阅读上面材料,解决下面问题:已知平面的方程为 , 直线是两平面与的交线,则直线与平面所成角的正弦值为( )A、0 B、 C、 D、
-
8、已知函数和的图象与直线交点的横坐标分别为a、b,则( )A、1 B、2 C、3 D、4
-
9、已知中, , , 是边上的动点.若平面 , , 且与面所成角的正弦值的最大值为 , 则三棱锥的外接球的表面积为( )A、 B、 C、 D、
-
10、“村超”是贵州榕江县乡村足球超级联赛的简称,是该县的一项传统乡村体育赛事,“村超”深受当地人民的喜爱,也在2023年开始火爆全网.某体育新闻网站派出含甲、乙在内的4名记者前去A,B,C三个足球场报道“村超”赛事,要求每个足球场至少1名记者,则甲、乙分在不同足球场的概率为( )A、 B、 C、 D、
-
11、设 , , , 则( )A、 B、 C、 D、
-
12、在△ABC中,角A,B,C所对的边分别为 a, b,c,已知 , 则cosB=( )A、 B、 C、 D、
-
13、已知椭圆(a>b>0)的离心率为 , 且四个顶点所围成的菱形的面积为4.(1)、求椭圆的标准方程;(2)、四边形ABCD的顶点在椭圆上,且对角线AC,BD过原点O,设 , 满足 .
①求证:直线AB和直线BC的斜率之和为定值;
②求四边形ABCD面积的最大值.
-
14、设函数的定义域为 , 对于区间 , 当且仅当函数满足以下①②两个性质中的任意一个时,则称区间是的一个“美好区间”.
性质①:对于任意 , 都有;
性质②:对于任意 , 都有.
(1)、已知 , .分别判断区间和区间是否为函数的“美好区间”,并说明理由;(2)、已知且 , 若区间是函数的一个“美好区间”,求实数的取值范围. -
15、如图,在三棱柱中,平面平面ABC, , , , , , .
 (1)、求证:B,D,E,四点共面;(2)、求二面角的余弦值.
(1)、求证:B,D,E,四点共面;(2)、求二面角的余弦值. -
16、某校为了了解学情,对各学科的学习兴趣作了问卷调查,经过数据整理得到下表:
语文兴趣
数学兴趣
英语兴趣
物理兴趣
化学兴趣
生物兴趣
答卷份数
350
470
380
400
300
500
兴趣良好频率
0.7
0.9
0.8
0.5
0.8
0.8
假设每份调查问卷只调查一科,各类调查是否达到良好的标准相互独立.
(1)、从收集的答卷中随机选取一份,求这份试卷的调查结果是英语兴趣良好的概率;(2)、从该校任选一位同学,试估计他在语文兴趣良好、数学兴趣良好、生物兴趣良好方面,至少具有两科兴趣良好的概率;(3)、按分层抽样的方法从参与物理兴趣和化学兴趣调查的同学中抽取7人,再从这7人中抽取3人,记3人中来自化学兴趣的人数为 , 求的分布列和期望. -
17、为数列的前项和.已知 , .
(1)证明是等比数列,并求数列的通项公式;
(2)数列为等差数列,且 , 求数列的前项和 .
-
18、我们称元有序实数组为维向量,为该向量的范数.已知维向量 , 其中 , 记范数为奇数的的个数为 , 则;(用含的式子表示,).
-
19、若 , 则 .
-
20、若公差不为0的等差数列的前四项和为10,且 , , 成等比数列,则 .