版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知函数 $f (x) = \frac{x + b - 1}{x^{2} + 1}$ （ $x \in [- 1, 1]$ ）是奇函数， $g (x) = x^{2} + (a - 2) x + 1$ 是偶函数.

(1)、求 $a + b$ ；

(2)、判断函数 $f (x)$ 在 $[- 1, 1]$ 上的单调性并说明理由；

(3)、若函数 $f (x)$ 满足不等式 $f (t - 1) + f (2 t) < 0$ ，求出 $t$ 的范围.

查看解析
2、已知函数 $f (x) = \sin x - \cos x (x \in R)$ ．

(1)、求函数 $f (x)$ 的单调递增区间；

(2)、求函数 $y = f^{2} (x) + \sqrt{3} \cos 2 x - 1, x \in [0, \frac{π}{2}]$ 的最大值与最小值．

查看解析
3、已知集合 $A = \{1, 2, 3\}$ ， $B = \{x |a x - 1 \geq 0\}$ .

(1)、当 $a = 2$ 时，求 $A \cap B$ 与 $A \cup B$ ；

(2)、若 $A \cap B = A$ ，求实数a的取值范围.

查看解析
4、若 $\sin α \cos α = - \frac{2}{5}$ ，则 $\tan α =$ .

查看解析
5、把函数 $y = \cos x$ 的图象上的所有点的横坐标缩小到原来的一半(纵坐标不变)，然后把图象向左平移 $\frac{π}{4}$ 个单位，则所得图形对应的函数解析式为.

查看解析
6、若 $f (x) = \{\begin{cases} - x + 2, x < 1 \\ \frac{a}{x}, x \geq 1 \end{cases}$ 是R上的减函数，则实数a的取值范围为.

查看解析
7、命题“ $\forall x \in [0, π]$ ， $\sin x \geq 0$ ”否定是.

查看解析
8、函数 $f (x) = A \sin (ω x + φ)$ 的图象如图所示，将函数 $f (x)$ 的图象向右平移 $\frac{π}{12}$ 个单位长度，得到 $y = g (x)$ 的图象，则下列说法正确的是（）

A、函数 $g (x)$ 的最大值为3 B、函数 $g (x)$ 关于点 $(\frac{π}{12}, 0)$ 对称 C、函数 $g (x)$ 在 $(0, \frac{π}{2})$ 上单调递减 D、函数 $g (x)$ 的最小正周期为 $π$

查看解析
9、若 $x > 0$ ， $y > 0$ ， $n \neq 0$ ， $m \in R$ ，则下列各式中，恒等的是（）

A、 $\lg x + \lg y = \lg (x + y)$ B、 $\lg \frac{x}{y} = \lg x - \lg y$ C、 $\log_{x^{m}} y^{n} = \frac{m}{n} \log_{x} y$ D、 $\lg x^{\frac{1}{n}} = \frac{\lg x}{n}$

查看解析
10、定义在 $(0, + \infty)$ 上的函数 $f (x)$ 满足：对 $\forall x_{1}, x_{2} \in (0, + \infty)$ ，且 $x_{1} \neq x_{2}$ ，都有 $\frac{x_{2} f (x_{1}) - x_{1} f (x_{2})}{x_{1} - x_{2}} > 0$ 成立，且 $f (2) = 4$ ，则不等式 $\frac{f (x)}{x} > 2$ 的解集为（）

A、 $(4, + \infty)$ B、 $(0, 4)$ C、 $(0, 2)$ D、 $(2, + \infty)$

查看解析
11、将函数 $f (x) = 4 \cos (\frac{π}{2} x)$ 和直线 $g (x) = x - 1$ 的所有交点从左到右依次记为A₁ ， A₂ ， A₃ ， …，A_n ，若P点坐标为（0，1），则 $|\overset{⃑}{P A_{1}} + \overset{⃑}{P A_{2}} + \dots + \overset{⃑}{P A_{n}}| =$ （）

A、 $5 \sqrt{2}$ B、 $3 \sqrt{2}$ C、 $\sqrt{2}$ D、0

查看解析
12、若角 $α$ ， $β$ 均为锐角， $\cos α = \frac{2 \sqrt{5}}{5}$ ， $\cos (α + β) = \frac{3}{5}$ ，则 $\sin β =$ （）

A、 $\frac{2 \sqrt{5}}{5}$ B、 $\frac{\sqrt{5}}{5}$ C、 $- \frac{\sqrt{5}}{5}$ D、 $- \frac{2 \sqrt{5}}{5}$

查看解析
13、函数① $y = a^{x}$ ；② $y = b^{x}$ ；③ $y = c^{x}$ ；④ $y = d^{x}$ 的图象如图所示，a，b，c，d分别是下列四个数： $\frac{5}{4}$ ， $\sqrt{3}$ ， $\frac{1}{3}$ ， $\frac{1}{2}$ 中的一个，则a，b，c，d的值分别是（）

A、 $\frac{5}{4}$ ， $\sqrt{3}$ ， $\frac{1}{3}$ ， $\frac{1}{2}$ B、 $\sqrt{3}$ ， $\frac{5}{4}$ ， $\frac{1}{3}$ ， $\frac{1}{2}$ C、 $\frac{1}{2}$ ， $\frac{1}{3}$ ， $\sqrt{3}$ ， $\frac{5}{4}$ ， D、 $\frac{1}{3}$ ， $\frac{1}{2}$ ， $\frac{5}{4}$ ， $\sqrt{3}$ ，

查看解析
14、将 $- 885^{\circ}$ 化为 $α + k \cdot 360^{\circ} (k \in Z, α \in [0^{\circ}, 360^{\circ}))$ 的形式是（）

A、 $- 165^{°} + (- 2) \times 360^{°}$ B、 $195^{°} + (- 3) \times 360^{°}$ C、 $195^{°} + (- 2) \times 360^{°}$ D、 $165^{°} + (- 3) \times 360^{°}$

查看解析
15、已知集合 $A = {x ∣ - 2 \leq x \leq 0}$ ， $B = {- 2, - 1, 0, 1, 2}$ ，则 $A \cap B =$ （）

A、 ${- 2, - 1, 0, 1, 2}$ B、 ${x ∣ - 2 \leq x \leq 2}$ C、 ${- 2, - 1, 0}$ D、 ${- 2 \leq x \leq 0}$

查看解析
16、某制药公司研制了一款针对某种病毒的新疫苗.该病毒一般通过病鼠与白鼠之间的接触传染，现有 $n$ 只白鼠，每只白鼠在接触病鼠后被感染的概率为 $\frac{1}{2}$ ，被感染的白鼠数用随机变量X表示，假设每只白鼠是否被感染之间相互独立

(1)、若 $P (X = 5) = P (X = 95)$ ，求数学期望 $E (X)$ ；

(2)、接种疫苗后的白鼠被病鼠感染的概率为 $p$ ，现有两个不同的研究团队理论研究发现概率 $p$ 与参数 $θ (0 < θ < 1)$ 的取值有关.团队A提出函数模型为 $p = \ln (1 + θ) - \frac{2}{3} θ^{2}$ ，团队B提出函数模型为 $p = \frac{1}{2} (1 - e^{- θ})$ .现将100只接种疫苗后的白鼠分成10组，每组10只，进行实验，随机变量 $X_{i} (i = 1, 2, \cdot \cdot \cdot, 10)$ 表示第 $i$ 组被感染的白鼠数，将随机变量 $X_{i} (i = 1, 2, \cdot \cdot \cdot, 10)$ 的实验结果 $x_{i} (i = 1, 2, \cdot \cdot \cdot, 10)$ 绘制成频数分布图，如图所示.

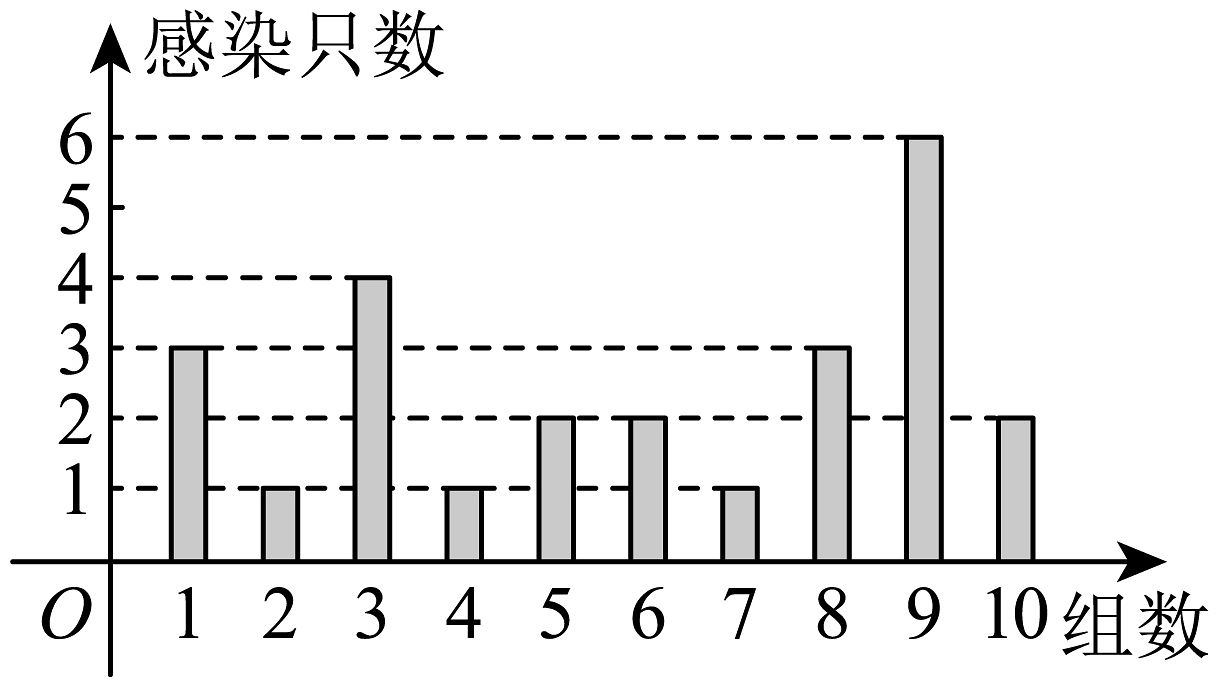
（i）试写出事件“ $X_{1} = x_{1}, X_{2} = x_{2}, \cdot \cdot \cdot, X_{10} = x_{10}$ ”发生的概率表达式（用 $p$ 表示，组合数不必计算）；
（ⅱ）在统计学中，若参数 $θ = θ_{0}$ 时使得概率 $P (X_{1} = x_{1}, X_{2} = x_{2}, \cdot \cdot \cdot, X_{10} = x_{10})$ 最大，称 $θ_{0}$ 是 $θ$ 的最大似然估计.根据这一原理和团队A，B提出的函数模型，判断哪个团队的函数模型可以求出 $θ$ 的最大似然估计，并求出最大似然估计.参考数据： $\ln \frac{3}{2} \approx 0.4055$ .

查看解析
17、若函数 $y = f (x)$ 满足 $f (x) = f (x + \frac{3 π}{2})$ 且 $f (\frac{π}{4} + x) = f (\frac{π}{4} - x) (x \in R)$ ，则称函数 $y = f (x)$ 为“M函数”．

(1)、试判断 $y = sin \frac{4}{3} x$ 是否为“M函数”，并说明理由；

(2)、函数 $g (x)$ 为“M函数”，其在 $x \in [- \frac{π}{2}, \frac{π}{4}]$ 的图象落在直线 $6 x + 8 y + 3 π = 0$ 上，在函数 $g (x)$ 图象上任取一点P，对于定点 $A (2024 π, 0)$ ，求线段AP的最小值；

(3)、函数 $f (x)$ 为“M函数”，且当 $x \in [\frac{π}{4},π]$ 时， $y = sin x$ ，求 $f (x)$ 的解析式；若当 $x \in [- \frac{π}{2}, \frac{5 π}{2}]$ ，关于x的方程 $f (x) = a$ （a为常数）有解，记该方程所有解的和为S，求S．

查看解析
18、亚运聚欢潮，璀璨共此时.2023年9月第19届亚洲运动会在杭州举办，来自亚洲45个国家和地区的1万多名运动员在这里团结交流、收获友谊，奋勇拼搏、超越自我，共同创造了亚洲体育新的辉煌和荣光，赢得了亚奥理事会大家庭和国际社会的广泛好评．亚运会圆满结束后，杭州某学校组织学生参加与本届亚运会有关的知识竞赛．为更好地了解该校学生对本届亚运会有关赛事和知识的掌握情况，采用随机抽样的方法抽取了600名学生进行调查，成绩全部分布在40~100分之间，根据调查的结果绘制的学生成绩频率分布直方图如图所示，

(1)、求频率分布直方图中 $a$ 的值；

(2)、估计这600名学生成绩的中位数；

(3)、根据频率分布直方图，按分层抽样的方法从成绩在 $[40, 60), [90, 100]$ 的学生中选取5人，再从这5人中任意选取2人，求这2人中至少有1人成绩不低于90分的概率．

查看解析
19、已知四边形 $A B C D$ 为直角梯形， $∠ A D C = 90^{\circ}, A D // B C, △ A B D$ 为等腰直角三角形，平面 $P A D ⊥$ 平面 $A B C D$ ， $E$ 为 $P A$ 的中点， $A D = 2 B C = 2 \sqrt{2}, P A = 3 P D = 3$ ．

(1)、求证： $A B ⊥$ 平面 $P B D$ ；

(2)、求三棱锥 $B - D E P$ 的体积．

查看解析
20、已知 $△ A B C$ 的内角A，B，C的对边分别是a，b，c， $B \in (\frac{π}{2},π), a = 3, b = 2 c$ ，且 $9 \sin B - 2 \sin C = 2 \sqrt{15}$ ，则 $△ A B C$ 的周长为.

查看解析

上一页 760 761 762 763 764 下一页跳转