版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知关于x的函数 $f (x) = \ln x - x + a$ ，其图象与x轴相切．

(1)、求 $f (x)$ 的表达式；

(2)、证明： $f (x) \leq 0$ ；

(3)、设数列 $a_{n} = \frac{1}{\ln (n + 1)}$ ，（ $n \in N^{*}$ ）， $\{a_{n}\}$ 的前n项和为 $S_{n}$ ，证明： $S_{n} > \frac{2 n}{n + 1} (n \in N^{*})$ ．

查看解析
2、如图，已知双曲线 $C : \frac{x^{2}}{a^{2}} - y^{2} = 1 (a ＞ 0)$ 的右焦点 $F$ ，点 $A ， B$ 分别在C的两条渐近线上， $A F ⊥ x$ 轴， $A B ⊥ O B ， B F / / O A$ （O为坐标原点）．

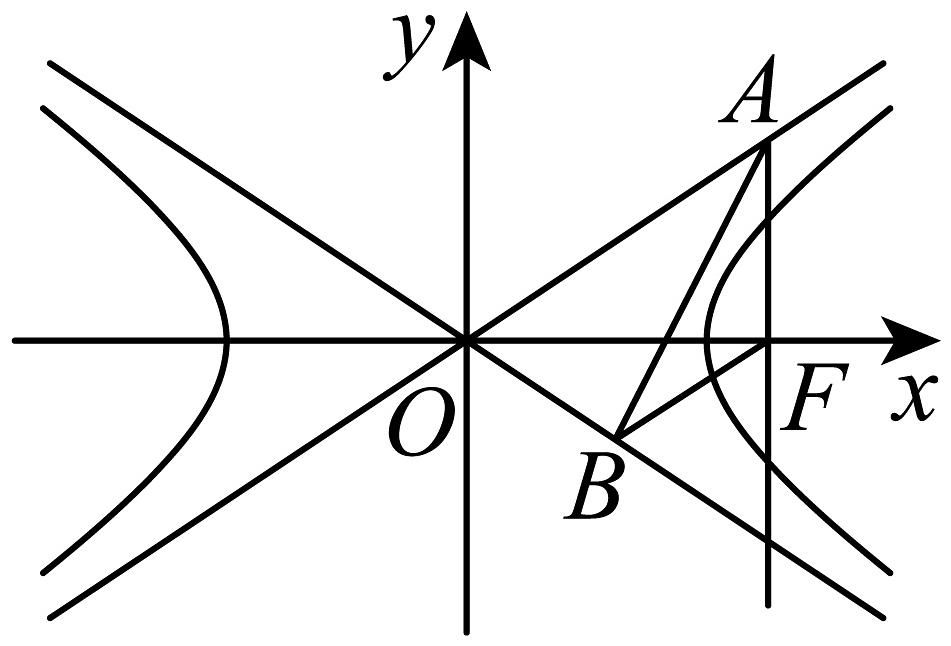(1)、求双曲线C的方程；

(2)、过C上一点 $P (x_{0}, y_{0})$ 的直线 $l ： \frac{x_{0} x}{a^{2}} - y_{0} y = 1$ 与直线AF相交于点M，与直线 $x = \frac{3}{2}$ 相交于点 $N$ ，证明点 $P$ 在 $C$ 上移动时， $\frac{|M F|}{|N F|}$ 恒为定值，并求此定值．

查看解析
3、已知篮球比赛中，得分规则如下：3分线外侧投入可得3分，踩线及3分线内侧投入可得2分，不进得0分；经过多次试验，某生投篮100次，有20个是3分线外侧投入，20个是踩线及3分线内侧投入，其余不能入篮，且每次投篮为相互独立事件．

(1)、求该生在4次投篮中恰有三次是3分线外侧投入的概率；

(2)、求该生两次投篮得分 $ξ$ 的分布列及数学期望．

查看解析
4、已知函数 $f (x) = (1 - \sqrt{3}) \cos^{2} x + \sin x \cos x + \sin (x + \frac{π}{4}) \sin (x - \frac{π}{4})$ ．

(1)、求f（x）的最小正周期；

(2)、若 $x \in [0, π]$ ，求f（x）的单调递增区间．

查看解析
5、如图，在四棱锥 $P - A B C D$ 中， $A C \cap B D = O$ ，底面ABCD为菱形，边长为2， $P C ⊥ B D$ ， $P A = P C$ ，且 $∠ A B C = 60^{°}$ ，异面直线PB与CD所成的角为 $60^{°}$ .

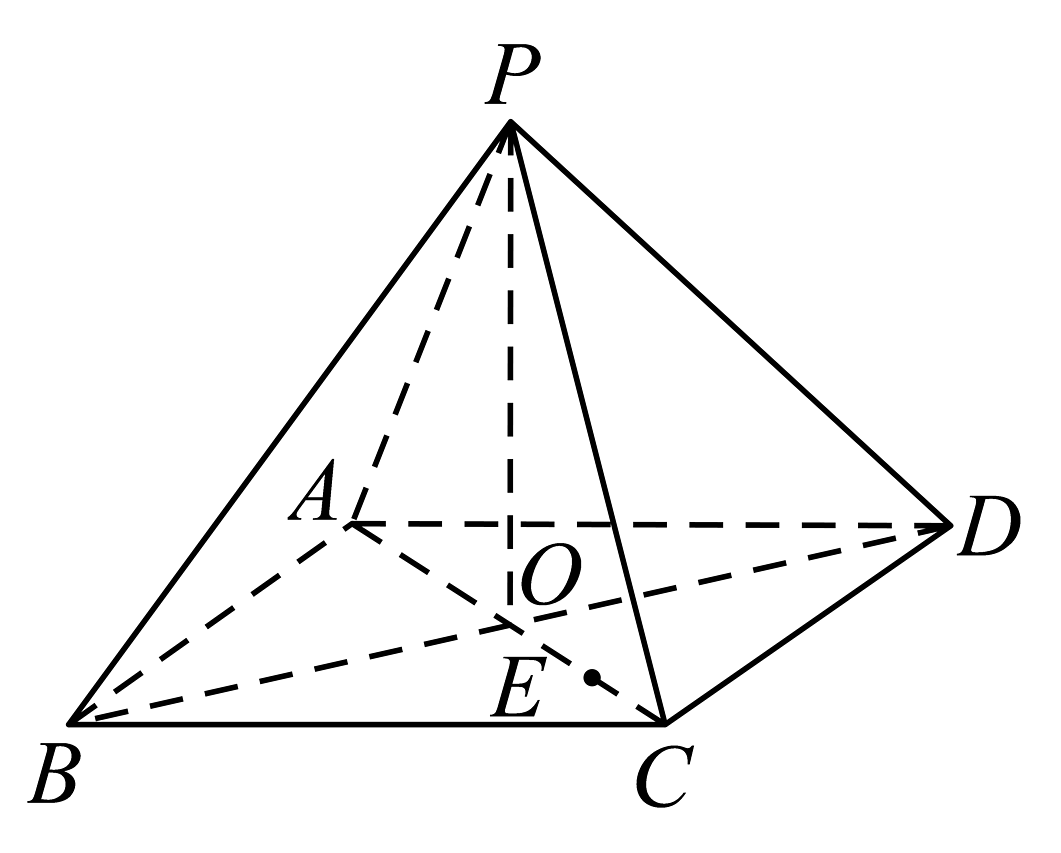(1)、求证： $P O ⊥$ 平面ABCD；

(2)、若E是线段OC的中点，求点E到直线BP的距离.

查看解析
6、在 $\begin{matrix} △ \end{matrix} A B C$ 中，内角 $A, B, C$ ，所对的边分别为 $a, b, c$ ，已知 $c = 1$ ， $\frac{sin B}{sin A} = b^{2} - a^{2} + 1$ ，且 $a \neq b$ ，则 $sin B - sin A$ 的最大值为．

查看解析
7、如果随机变量 $ξ \sim B (n, p)$ ，且 $E (2 ξ) = 24, D (ξ) = 8$ ，则 $p =$ .

查看解析
8、在复平面内，若复数z对应的点为 $(1, 3)$ ，则（）

A、 $z + \bar{z} = 2$ B、 $z^{2} = 10$ C、 $z \bar{z} = 10$ D、 $|z - \frac{z}{1 + i}| = 5$

查看解析
9、 $\forall x \in R$ ，用 $M (x)$ 表示 $f (x), g (x)$ 中的较小者，记为 $M (x) = \min {f (x), g (x)}$ ，设函数 $f (x) = e^{x - 1} + x - 2, g (x) = - x^{2} + (a - 1) x - a$ ，若 $\forall x \in R, M (x) \leq 0$ ，则a的取值范围为（）

A、 $(- \infty, 3 + 2 \sqrt{2}]$ B、 $(- \infty, 6]$ C、 $[3 - 2 \sqrt{2}, 3 + 2 \sqrt{2}]$ D、 $[3 - 2 \sqrt{2}, + \infty)$

查看解析
10、已知圆O是圆心为原点的单位圆，A，B是圆O上任意两个不同的点， $M (2, 0)$ ，则 $| \vec{M A} + \vec{M B} |$ 的取值范围为（）

A、 $(1, 2)$ B、 $(1, 3)$ C、 $(2, 4)$ D、 $(2, 6)$

查看解析
11、某研究小组为了解某市高中生自主阅读情况，随机调查了2000名学生的每周自主阅读时间，按照时长（单位：小时）分成五组： $[2, 4), [4, 6), [6, 8), [8, 10), [10, 12)$ ，得到如图所示的频率分布直方图，其中每周自主阅读时间不低于8小时的频率为0.3.则以下说法中错误的是（）

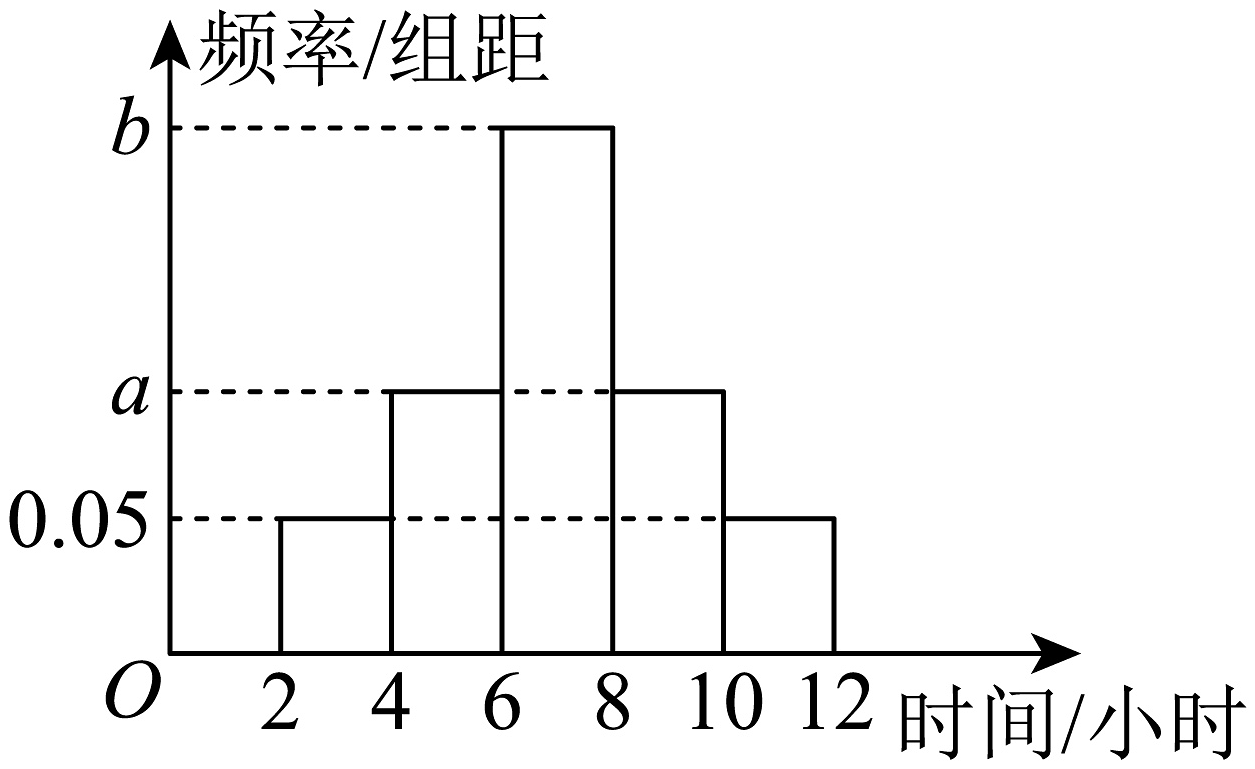A、 $a + b = 0.30$ B、估计样本数据的第60百分位数值是7.5小时 C、样本的极差介于6小时至10小时之间 D、估计这2000名学生每周自主阅读时间的平均值是6.5小时

查看解析
12、下列命题中错误的命题是（）

A、设等比数列 $\{a_{n}\}$ 的前n项和为 $S_{n}$ ，则“ $a_{1} > 0$ ”是“ $S_{3} > S_{2}$ ”的充分必要条件； B、对于命题p： $\exists x_{0} \in R$ ，使得 $x_{0}^{2} - 1 \leq 0$ ，则 $\neg p : \forall x \in R$ ，都有 $x^{2} - 1 > 0$ ； C、设函数 $f (x) = x - \sin x (x \in R)$ ，则函数f（x）有三个不同的零点； D、若随机变量 $X ~ N (2, σ^{2})$ ，则 $P (X > 2) = 0.5$ ；

查看解析
13、某外商计划在5个候选城市投资3个不同的项目，且在同一个城市投资的项目不超过2个，则该外商不同的投资方案有（）

A、36种 B、60种 C、120种 D、180种

查看解析
14、已知等比数列 $\{a_{n}\}$ 的公比与等差数列 $\{b_{n}\}$ 的公差均为2，且 $a_{1} = b_{1} + 2 = 2$ ，设数列 $\{c_{n}\}$ 满足 $c_{n} = \{\begin{array}{l} a_{n}, n 为奇数 \\ b_{n}, n 为偶数 \end{array}$ ， $n \in N^{*}$ ，则数列 $\{c_{n}\}$ 的前20项的和为（）

A、 $\frac{598 - 2^{21}}{3}$ B、 $\frac{598 + 2^{21}}{3}$ C、 $\frac{602 + 2^{20}}{3}$ D、 $\frac{602 + 2^{21}}{3}$

查看解析
15、已知点 $P (m, - 2)$ 在函数 $y = \log_{\frac{1}{3}} x$ 的图象上，点A的坐标是 $(4, 3)$ ，那么 $| \vec{A P} |$ 的值是（）

A、 $\sqrt{10}$ B、 $2 \sqrt{10}$ C、 $6 \sqrt{2}$ D、 $5 \sqrt{2}$

查看解析
16、设全集 $U = R$ ，集合 $A = \{x | x < 2\}$ ， $B = \{x | x < 1\}$ ，则集合 $(∁_{U} A) \cup B =$ （）

A、 $(- \infty, 2)$ B、 $[2, + \infty)$ C、 $(1, 2)$ D、 $(- \infty, 1) \cup [2, + \infty)$

查看解析
17、已知直线 $l_{1} : 2 x + a^{2} y - 1 = 0$ 与直线 $l_{2} : 3 a x - y + 9 = 0$ ，则“ $a = 6$ ”是 $l_{1} ⊥ l_{2}$ 的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、即不充分也不必要条件

查看解析
18、双曲余弦函数 $cosh x = \frac{e^{x} + e^{- x}}{2}$ ，双曲正弦函数 $sinh x = \frac{e^{x} - e^{- x}}{2}$ ．

(1)、求函数 $cosh x = \frac{e^{x} + e^{- x}}{2}$ 的单调增区间；

(2)、若函数 $y = cosh 2 x - a sinh x$ 在 $[0, + \infty)$ 上的最小值是 $\frac{1}{4}$ ，求实数a的值；

(3)、对任意 $x \in R, cosh (x) \geq cos x + m x^{2}$ 恒成立，求实数m的取值范围．

查看解析
19、已知椭圆的左、右焦点分别为 $F_{1} (- 1, 0)$ ， $F_{2} (1, 0)$ ，且经过点 $P (- 1, \frac{3}{2})$ ．

(1)、求该椭圆的离心率；

(2)、点Q为椭圆上一点，且位于第三象限，若 $△ P Q F_{2}$ 的面积为3，求点Q的坐标；

(3)、A，B，C，D是椭圆上不重合的四个点，AB与CD相交于点 $F_{1}$ ，且 $\vec{A B} \cdot \vec{C D} = 0$ ，求 $|A B| + |C D|$ 的取值范围．

查看解析
20、2024年第七届中国国际进口博览会（简称进博会）于11月5日至10日在上海国家会展中心举行.为了解进博会参会者的年龄结构，某机构随机抽取了年龄在15-75岁之间的200名参会者进行调查，并按年龄绘制了频率分布直方图，分组区间为 $[15, 25), [25, 35), [35, 45), [45, 55), [55, 65), [65, 75]$ .把年龄落在区间 $[15, 35)$ 内的人称为“青年人”，把年龄落在区间 $[35, 65)$ 内的人称为“中年人”，把年龄落在 $[65, 75]$ 内的人称为“老年人”.

(1)、求所抽取的“青年人”的人数；

(2)、以分层抽样的方式从“青年人”“中年人”“老年人”中抽取10名参会者做进一步访谈，发现其中女性共4人，这4人中有3人是“中年人”.再用抽签法从所抽取的10名参会者中任选2人.
①简述如何采用抽签法任选2人；
②设事件A：2人均为“中年人”，事件B：2人中至少有1人为男性，判断事件A与事件B是否独立，并说明理由.

查看解析

上一页 754 755 756 757 758 下一页跳转