相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、黎曼函数(Riemann function)是一个特殊的函数,由德国数学家黎曼发现并提出,其基本定义是:(注:分子与分母是互质数的分数,称为既约分数),若是奇函数,且 , 当时, , 则( )A、 B、 C、 D、
-
2、如图的曲线是幂函数在第一象限内的图象.已知分别取四个值,与曲线相应的依次为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、函数的零点为1,2,则不等式的解集为( )A、 B、或 C、或 D、
-
4、已知集合 , , 则( )A、 B、 C、 D、
-
5、在平面内,若直线将多边形分为两部分,且多边形在两侧的顶点到的距离之和相等,则称为多边形的一条“等线”.已知双曲线与双曲线有相同的离心率,、分别为双曲线的左、右焦点,为双曲线右支上一动点,双曲线在点处的切线与双曲线的渐近线交于、两点(在上方),当轴时,直线为的等线.(1)、求双曲线的方程;(2)、若是四边形的等线,求四边形的面积;(3)、已知为坐标原点,直线与双曲线的右支交于点 , 试判断双曲线在点处的切线是否为的等线,请说明理由.
【注】双曲线在其上一点处的切线方程为.
-
6、已知动点到点的距离比它到直线的距离小 , 记动点的轨迹为.(1)、求轨迹的方程.(2)、已知直线与轨迹交于A,B两点,以A,B为切点作两条切线,分别为 , , 且 , 相交于点.若 , 求.
-
7、已知的顶点 , , 顶点满足 , 记顶点的轨迹为.(1)、求曲线的方程.(2)、过点的直线(斜率不为0)与曲线交于不同的两点P,Q,O为坐标原点,试判断直线OP,OQ的斜率之积是否为定值.若为定值,求出该定值;若不是,说明理由.
-
8、已知椭圆上的点到其焦点的距离的最大值为16,最小值为4.(1)、求椭圆的方程;(2)、直线与椭圆相交于A,B两点,若线段AB的中点坐标为 , 求直线的方程.
-
9、双曲线以椭圆的焦点为顶点,长轴的顶点为焦点,则双曲线的标准方程为 , 渐近线方程为.
-
10、已知向量 , 则在上的投影向量的模为.
-
11、已知椭圆的左、右焦点分别为 , , 是上任意一点,则下列结论正确的是( )A、若存在点 , 使得 , 则椭圆的离心率的取值范围为 B、若存在点 , 使得 , 则椭圆的离心率的取值范围为 C、若存在点 , 使得 , 且 , 则椭圆的离心率为 D、若存在点 , 使得 , 且 , 则椭圆的离心率为
-
12、已知直线 , 直线 , 圆 , 则下列选项正确的是( )A、若 , 则 B、若 , 则 C、若与圆相交于 , 两点,则 D、过上一点向圆作切线,切点为 , 则
-
13、过抛物线的焦点作圆的切线,该切线交抛物线C于A,B两点,则( )A、 B、14 C、15 D、16
-
14、在正方体中, , , 则( )A、 B、 C、 D、
-
15、已知椭圆 , 其中离心率为 , 且过点(1)、求椭圆的标准方程;(2)、过点的直线被椭圆截得的弦长为 , 求直线的方程.
-
16、如图所示,已知直四棱柱中,底面是边长为2的菱形,且 , , , , 分别是 , , 的中点,则异面直线 , 所成角的余弦值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、在平面直角坐标系中,△ABC的三个顶点坐标分别为 , , .(1)、求BC边上的中线AD的所在直线方程;(2)、求△ABC的外接圆O被直线l:截得的弦长.
-
18、如图,平行六面体中, , , , .
 (1)、以向量为基底表示向量 , 求对角线的长度;(2)、求异面直线与所成角的余弦值.
(1)、以向量为基底表示向量 , 求对角线的长度;(2)、求异面直线与所成角的余弦值. -
19、已知为双曲线的两个焦点,为双曲线上任意一点,则( )A、 B、双曲线的渐近线方程为 C、双曲线的离心率为 D、
-
20、如图①,在中, , , E,F分别为AB,AC上的点, , . 如图②,将沿EF折起,当四棱锥的体积最大时,点E到平面ACF的距离为( )
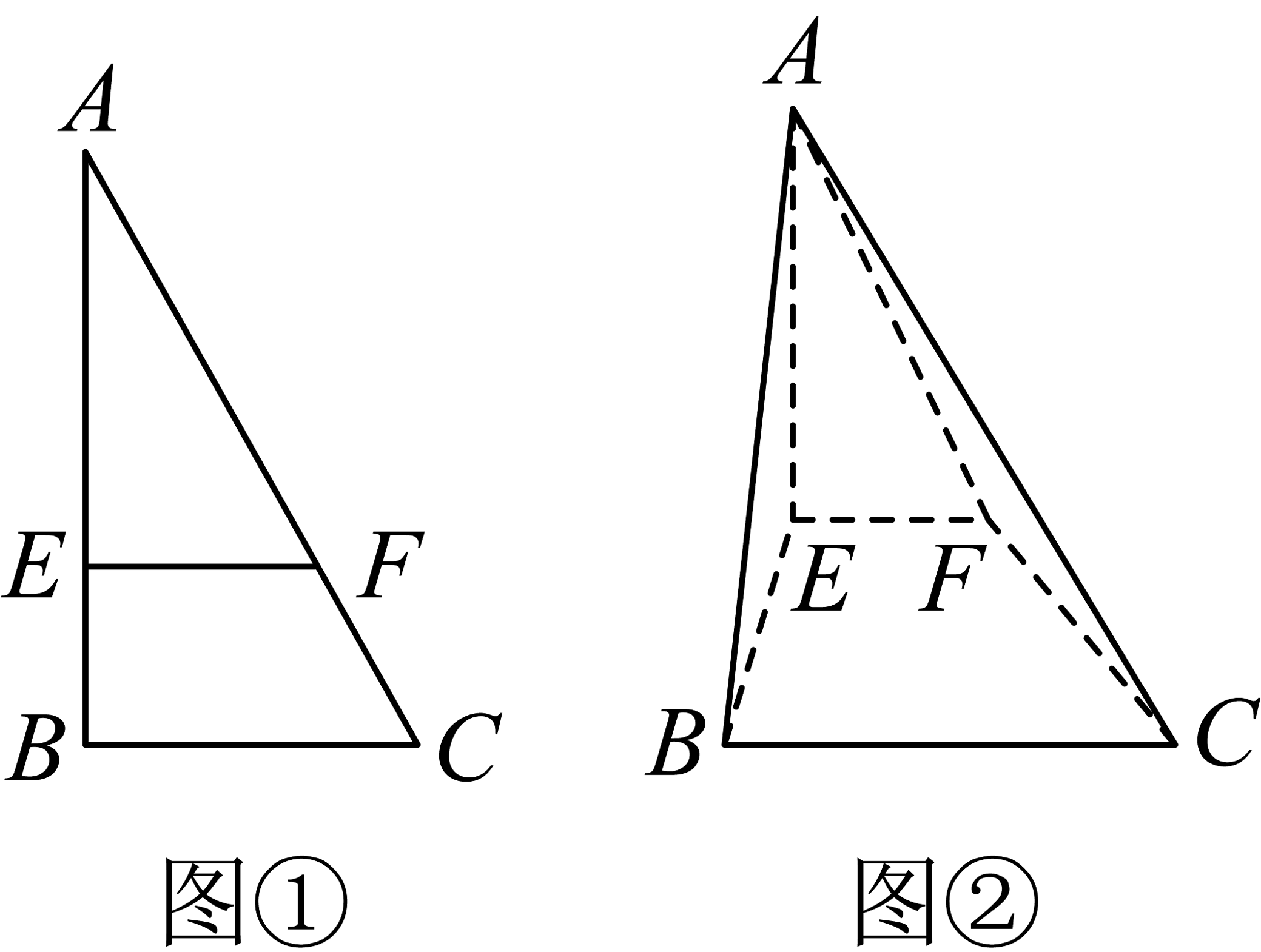 A、 B、 C、 D、
A、 B、 C、 D、