版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、若复数 $z = \frac{5}{i - 2}$ ， $z$ 的虚部为（）

A、 $i$ B、1 C、 $- 1$ D、 $- i$

查看解析
2、在 $△ A B C$ 中，内角 $A, B, C$ 的对边分别为 $a, b, c$ ，且 $\frac{a^{2}}{b^{2}} = \frac{a^{2} + c^{2} - b^{2}}{b^{2} + c^{2} - a^{2}} \neq 1$ ，则 $A + B =$ （）

A、 $\frac{π}{2}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{π}{6}$

查看解析
3、下列说法正确的是（）

A、命题“ $\forall x > 1, x^{2} < 1$ ”的否定是“ $\exists x \leq 1, x^{2} \geq 1$ ” B、“ $a > 1$ ”是“ $\frac{1}{a} < 1$ ”的充分不必要条件 C、设 $a, b \in R$ ，则“ $a \neq 0$ ”是“ $a b \neq 0$ ”的必要不充分条件 D、“ $x > 1$ ”是“ $|x + 1| \geq 2$ ”的既不充分也不必要条件

查看解析
4、已知函数 $f (x) = 2 x^{3} - 3 x^{2}$ ，则（）

A、 $x = 0$ 是 $f (x)$ 的极大值点 B、 $f (x)$ 的图象关于点 $(\frac{1}{2}, \frac{1}{2})$ 对称 C、 $g (x) = f (x) + 1$ 有2个零点 D、当 $0 < x < 1$ 时， $f (x^{2} - 1) > f (x - 1)$

查看解析
5、已知集合 $A = \{x| x - 3 > 0\}$ ， $B = \{x| x^{2} - 5 x + 4 > 0\}$ ，则 $A \cap B =$ （）

A、 $(- \infty, 1)$ B、 $(- \infty, 3)$ C、 $(3, + \infty)$ D、 $(4, + \infty)$

查看解析
6、甲、乙、丙三人结伴去游乐园玩射击游戏，其中甲射击一次击中目标的概率为 $\frac{1}{2}$ ，甲、乙两人各射击一次且都击中目标的概率为 $\frac{1}{6}$ ，乙、丙两人各射击一次且都击中目标的概率为 $\frac{1}{9}$ ，且任意两次射击互不影响．

(1)、分别计算乙，丙两人各射击一次击中目标的概率；

(2)、求甲、乙、丙各射击一次恰有一人击中目标的概率；

(3)、若乙想击中目标的概率不低于 $\frac{99}{100}$ ，乙至少需要射击多少次？（参考数据： $\lg 2 \approx 0.3010$ ， $\lg 3 \approx 0.4771$ ）

查看解析
7、已知向量 $\vec{a} = (1, \sqrt{3})$ ， $\vec{b} = (0 ， 1)$ ，则 $\vec{b}$ 在 $\vec{a}$ 方向上的投影向量等于.

查看解析
8、正整数集 $A = \{m + 1, m + 2, m + 3, \dots, m + 3 n\}$ ，其中 $m \in N, n \in N^{+}$ .将集合 $A$ 拆分成 $n$ 个三元子集，这 $n$ 个集合两两没有公共元素.若存在一种拆法，使得每个三元子集中都有一个数等于其他两数之和，则称集合 $A$ 是“三元可拆集”.

(1)、若 $m = 1, n = 3$ ，判断集合 $A$ 是否为“三元可拆集”，若是，请给出一种拆法；若不是，请说明理由；

(2)、若 $m = 0, n = 6$ ，证明：集合 $A$ 不是“三元可拆集”；

(3)、若 $n = 16$ ，是否存在 $m$ 使得集合 $A$ 是“三元可拆集”，若存在，请求出 $m$ 的最大值并给出一种拆法；若不存在，请说明理由.

查看解析
9、已知 $b > 0$ ，函数 $f (x) = x^{2} - x - (x - 1) ln (b x)$ 在点 $(1, f (1))$ 处的切线过点 $(0, - 1)$ .

(1)、求实数b的值；

(2)、证明： $f (x)$ 在 $(0, + \infty)$ 上单调递增；

(3)、若对 $\forall x \geq 1, f (x) \geq a (x - 1)$ 恒成立，求实数a的取值范围．

查看解析
10、已知 $P (x_{0}, y_{0})$ 是曲线 $C : x^{3} + y^{3} = y - x$ 上的一点，则下列选项中正确的是（）

A、曲线 $C$ 的图象关于原点对称 B、对任意 $x_{0} \in R$ ，直线 $x = x_{0}$ 与曲线 $C$ 有唯一交点 $P$ C、对任意 $y_{0} \in [- 1, 1]$ ，恒有 $|x_{0}| < \frac{1}{2}$ D、曲线 $C$ 在 $- 1 \leq y \leq 1$ 的部分与 $y$ 轴围成图形的面积小于 $\frac{π}{4}$

查看解析
11、已知抛物线 $C : y^{2} = 2 p x (p > 0)$ ，过 $C$ 的焦点 $F$ 作直线 $l : x = t y + 1$ ，若 $C$ 与 $l$ 交于 $A, B$ 两点， $\vec{A F} = 2 \vec{F B}$ ，则下列结论正确的有（）

A、 $p = 2$ B、 $|A F| = 3$ C、 $t = 2 \sqrt{2}$ 或 $- 2 \sqrt{2}$ D、线段 $A B$ 中点的横坐标为 $\frac{5}{4}$

查看解析
12、已知函数 $f (x) = 2 {cos}^{2} ω x - {(sin ω x - cos ω x)}^{2} (ω > 0)$ 的图象关于直线 $x = \frac{π}{12}$ 轴对称，且 $f (x)$ 在 $(0, \frac{π}{3})$ 上没有最小值，则 $ω$ 的值为（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{3}{2}$ D、2

查看解析
13、已知集合 $A = {(x, y) | y = | x |}, B = \{(x, y) | y = \frac{1}{| x |}\}$ ，则 $A \cap B =$ （）

A、 ${- 1, 1}$ B、 ${(- 1, 1), (1, 1)}$ C、 $(0, + \infty)$ D、 $(0, 1)$

查看解析
14、已知函数 $f (x) = A sin (ω x + φ) (A > 0, ω > 0, |φ| < \frac{π}{2})$ 的部分图象如图所示，则下列说法正确的是（）

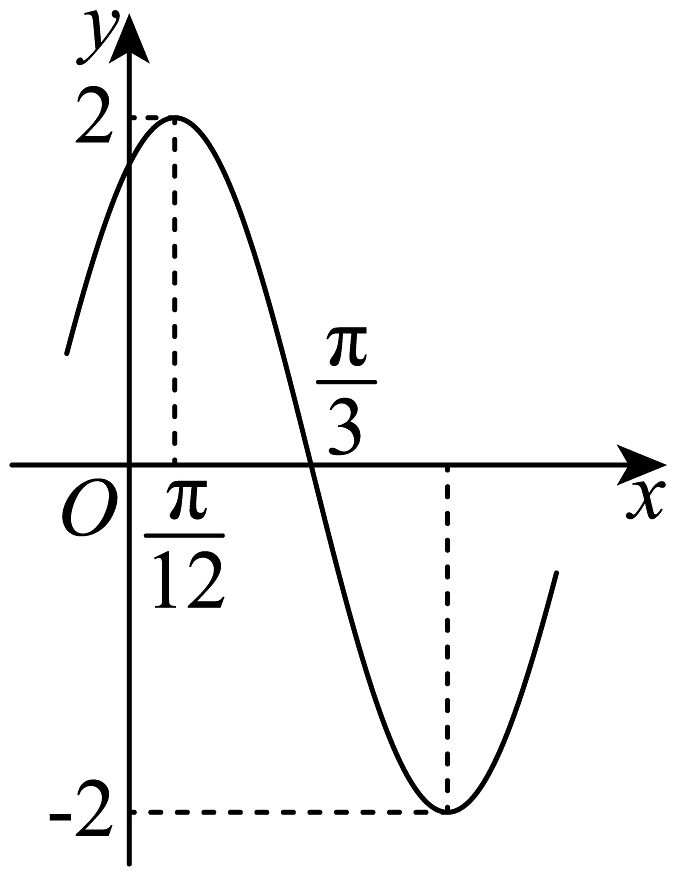A、 $ω = 2$ B、函数 $f (x)$ 的图象关于直线 $x = - \frac{5}{12} π$ 对称 C、函数 $f (x - \frac{2 π}{3})$ 是偶函数 D、将函数 $f (x)$ 图象上所有点的横坐标变为原来的2倍，得到函数 $y = 2 sin (x + \frac{π}{3})$ 的图象

查看解析
15、《瀑布》（图1）是最为人所知的作品之一，图中的瀑布会源源不断地落下，落下的水又逆流而上，荒唐至极，但又会让你百看不腻，画面下方还有一位饶有兴致的观察者，似乎他没发现什么不对劲.此时，他既是画外的观看者，也是埃舍尔自己.画面两座高塔各有一个几何体，左塔上方是著名的“三立方体合体”由三个正方体构成，右塔上的几何体是首次出现，后称“埃舍尔多面体”（图2）
埃舍尔多面体可以用两两垂直且中心重合的三个正方形构造，设边长均为2，定义正方形 $A_{n} B_{n} C_{n} D_{n}$ ， $n = 1, 2, 3$ 的顶点为“框架点”，定义两正方形交线为“极轴”，其端点为“极点”，记为 $P_{n}, Q_{n}$ ，将极点 $P_{1}, Q_{1}$ ，分别与正方形 $A_{2} B_{2} C_{2} D_{2}$ 的顶点连线，取其中点记为 $E_{m}$ ， $F_{m}$ ， $m = 1, 2, 3, 4$ ，如（图3）.埃舍尔多面体可视部分是由12个四棱锥构成，这些四棱锥顶点均为“框架点”，底面四边形由两个“极点”与两个“中点”构成，为了便于理解，图4我们构造了其中两个四棱锥 $A_{1} - P_{1} E_{1} P_{2} E_{2}$ 与 $A_{2} - P_{2} E_{1} P_{3} F_{1}$

(1)、求异面直线 $P_{1} A_{2}$ 与 $Q_{1} B_{2}$ 成角余弦值；

(2)、求平面 $P_{1} A_{1} E_{1}$ 与平面 $A_{1} E_{2} P_{2}$ 的夹角正弦值；

(3)、求埃舍尔体的表面积与体积（直接写出答案）.

查看解析
16、从出游方式看，春节期间是家庭旅游好时机．某地区消费者协会调查了部分2024年春节以家庭为单位出游支出情况，统计得到家庭旅游总支出（单位：百元）频率分布直方图，如图所示．（同一组中的数据用该组区间的中点值为代表）

(1)、求 $a$ 的值；

(2)、估计家庭消费总支出的第75百分位数．

(3)、从 $［ 60, 70 ）$ 和 $［ 80, 90 ）$ 两组中用分层抽样的方法共抽取了6人，再从这6人中随机抽取2人，求所抽取的2人来自同一组的概率．

查看解析
17、对于任意实数 $x$ ， $[x]$ 表示不超过 $x$ 的最大整数，如 $[1.1] = 1$ ， $[- 1.2] = - 2$ ，定义在 $R$ 上的函数 $f (x) = [2 x] + [3 x]$ ，若 $A = {y | y = f (x)$ ， $0 \leq x \leq 1}$ ，则 $A$ 中所有元素的和为．

查看解析
18、甲、乙两人投篮，每次由其中一人投篮，规则如下：若命中则此人继续投篮，若末命中则换为对方投篮．无论之前投篮情况如何，甲每次投篮的命中率均为0.6，乙每次投篮的命中率均为0.8．由抽签确定第1次投篮的人选，第1次投篮的人是甲、乙的概率各为0.5．

(1)、求第2次投篮的人是乙的概率；

(2)、求第 $i$ 次投篮的人是甲的概率；

(3)、已知：若随机变量 $X_{i}$ 服从两点分布，且 $P (X_{i} = 1) = 1 - P (X_{i} = 0) = q_{i}, i = 1, 2, \cdot \cdot \cdot, n$ ，则 $E (\sum_{i = 1}^{n} X_{i}) = \sum_{i = 1}^{n} q_{i}$ ．记前 $n$ 次（即从第1次到第 $n$ 次投篮）中甲投篮的次数为 $Y$ ，求 $E (Y)$ ．

查看解析
19、已知空间向量 $\overset{⃑}{a} = (m + 1, m, - 2)$ ， $\overset{⃑}{b} = (- 2, 1, 4)$ ，且 $\overset{⃑}{a} ⊥ \overset{⃑}{b}$ ，则 $m$ 的值为（）

A、 $- \frac{10}{3}$ B、 $- 10$ C、 $10$ D、 $\frac{10}{3}$

查看解析
20、判断下列各组直线是否平行，并说明理由．

(1)、 $l_{1}$ 经过点 $A (2, 3), B (- 4, 0)$ ， $l_{2}$ 经过点 $M (- 3, 1), N (- 2, 2)$ ；

(2)、 $l_{1}$ 的斜率为 $- 10$ ， $l_{2}$ 经过点 $A (10, 2), B (20, 3)$ .

查看解析

上一页 935 936 937 938 939 下一页跳转