相关试卷
- 河北省张家口市2016-2017学年高一下学期数学期末考试试卷
- 河北省邢台市2016-2017学年高一下学期数学期末考试试卷
- 河北省唐山市2016-2017学年高一下学期数学期末考试试卷
- 河北省廊坊市省级示范高中联合体2016-2017学年高一下学期数学期末考试试卷
- 河北省衡水市深州中学2016-2017学年高一下学期数学期末考试试卷
- 河北省邯郸市2016-2017学年高一下学期数学期末考试试卷
- 河北省承德市2016-2017学年高一下学期数学期末考试试卷
- 河北省保定市2016-2017学年高一下学期数学期末考试试卷
- 江西省赣州市2016-2017学年高一下学期期末数学考试试卷
- 四川省雅安市2016-2017学年高二下学期数学期末考试试卷(文科)
-
1、已知曲线 , 则下列结论正确的是( )A、当时,曲线是椭圆 B、当或时,曲线是双曲线 C、若曲线是焦点在轴上的椭圆,则 D、若曲线是焦点在轴上的双曲线,则
-
2、已知直线过点交抛物线于两相异点,点关于轴的对称点为 , 过原点作直线的垂线,垂足为 , 则点的轨迹方程为( )A、 B、 C、 D、
-
3、斐波那契数列因数学家莱昂纳多•斐波那契(LeonardodaFibonaci)以兔子繁殖为例而引入,故又称为“兔子数列”.在数学上,斐波那契数列由以下递推方法定义:数列满足 , 则( )A、 B、 C、 D、
-
4、正方体中,分别是的中点,点是线段(含端点)上的动点,当由点运动到点时,三棱锥的体积( )A、先变大后变小 B、先变小后变大 C、不变 D、无法判断
-
5、已知椭圆 , 过原点且倾斜角为的直线交椭圆于两点,则( )A、 B、 C、 D、
-
6、已知直线 , 圆 , 则直线与圆的位置关系是( )A、相交 B、相切 C、相离 D、以上都有可能
-
7、已知平面平面的法向量分别为 , 则实数( )A、3 B、-3 C、2 D、-2
-
8、下列方程所表示的直线中,倾斜角为的是( )A、 B、 C、 D、
-
9、命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,
-
10、已知函数.(1)、判断奇偶性并证明;(2)、利用定义证明在R上单调递增;(3)、若存在实数 , 使得成立,求实数k的取值范围.
-
11、已知正数满足 , 则( )A、 B、 C、 D、
-
12、函数的值域是( )A、 B、 C、 D、
-
13、一游戏规则如下:一个质点在数轴上运动,从原点出发,每次向左或者向右移动一个单位,共移动了次.(1)、已知质点每次向右移动的概率为.
①当 时,求质点最终回到原点的概率;
②规定质点在运动过程中,只要出现在原点左侧,游戏就结束,否则游戏就继续、直到移动了次,分别求出当和时质点最终落在原点右侧的概率并比较它们的大小
(2)、现在规定游戏分为两个阶段:第一阶段,质点每次向右移动的概率为、共移动了3次、若质点最终落在了原点左侧,则结束游戏,且最终得分为0分. 若最终落在了原点右侧、则通过第一阶段,并进入第二阶段:质点重新回到原点,每次向右移动的概率为 , 并再次移动了3次,若质点最终落在了原点左侧,则最终得分也为0分; 若最终落在了原点右侧,则最终得分为质点位于数轴上所在位置对应的实数.①请用含的式子表示该游戏得分的数学期望;
②若 则当取何值的时候,该游戏得分的期望值最大?
-
14、已知函数 , .(1)、若在区间上最大值为2,求实数的值;(2)、当时,求不等式的解集.
-
15、在四棱锥中,底面 , , , , , 点为棱中点.
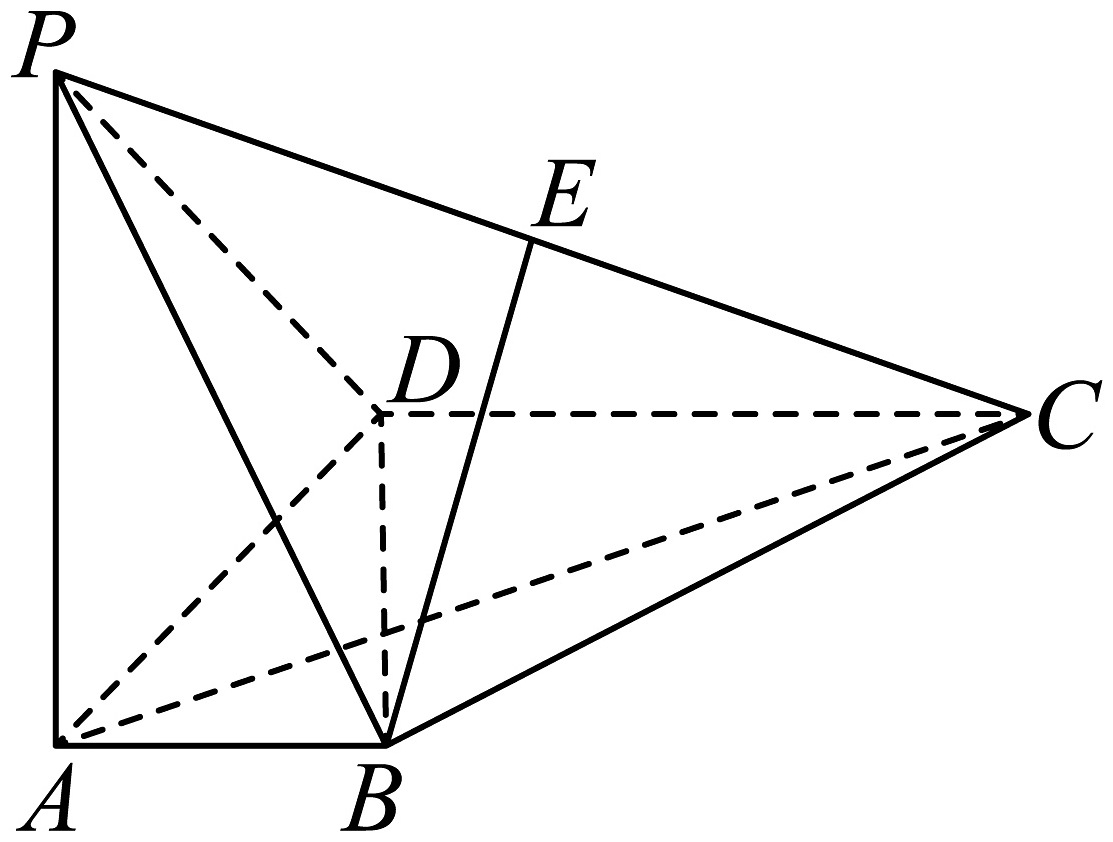 (1)、证明:平面;(2)、求直线与平面所成角的正弦值;(3)、若为棱上一点,满足 , 求平面与平面夹角的余弦值.
(1)、证明:平面;(2)、求直线与平面所成角的正弦值;(3)、若为棱上一点,满足 , 求平面与平面夹角的余弦值. -
16、如图,平行六面体中,AC与BD交于点M,设 , , , 则( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、下列各组函数表示同一函数的是( )A、 B、 C、 D、
-
18、由直线上的一点向圆引切线,切点为 , 则的最小值为.
-
19、已知直线经过点 , 且是的方向向量,则点到的距离为 .
-
20、已知 , 分别是平面 , 的法向量,且 , 则t的值为( )A、1 B、2 C、 D、