相关试卷
- 河北省张家口市2016-2017学年高一下学期数学期末考试试卷
- 河北省邢台市2016-2017学年高一下学期数学期末考试试卷
- 河北省唐山市2016-2017学年高一下学期数学期末考试试卷
- 河北省廊坊市省级示范高中联合体2016-2017学年高一下学期数学期末考试试卷
- 河北省衡水市深州中学2016-2017学年高一下学期数学期末考试试卷
- 河北省邯郸市2016-2017学年高一下学期数学期末考试试卷
- 河北省承德市2016-2017学年高一下学期数学期末考试试卷
- 河北省保定市2016-2017学年高一下学期数学期末考试试卷
- 江西省赣州市2016-2017学年高一下学期期末数学考试试卷
- 四川省雅安市2016-2017学年高二下学期数学期末考试试卷(文科)
-
1、已知圆:和圆: , 则两圆公共弦所在直线的方程为.
-
2、如图,在中, , , , 过中点的直线与线段交于点 . 将沿直线翻折至 , 且点在平面内的射影在线段上,连接交于点 , 是直线上异于的任意一点,则( )
 A、 B、 C、点的轨迹的长度为 D、直线与平面所成角的余弦值的最小值为
A、 B、 C、点的轨迹的长度为 D、直线与平面所成角的余弦值的最小值为 -
3、数列2,0,2,0,…的通项公式可以是( )A、 B、 C、 D、
-
4、已知双曲线C:( , )的左、右焦点分别为 , , 过的直线分别交双曲线左、右两支于A、B两点,点C在x轴上, , 平分 , 则双曲线C的离心率为( )A、 B、 C、 D、
-
5、一个半径为1的小球在一个内壁棱长为的正四面体封闭容器内可向各个方向自由运动,则该小球表面永远不可能接触到的容器内壁的面积是( )A、 B、 C、 D、
-
6、展开式中的常数项为( )A、15 B、60 C、 D、240
-
7、 , , , 若 , , 共面,则实数k为( )A、1 B、2 C、3 D、4
-
8、已知是关于复数z的方程(m,)的一根,则( )A、5 B、6 C、7 D、8
-
9、已知为复数,则下列说法正确的是( )A、 B、 C、若 , 则 D、若 , 则或
-
10、如图,八面体的每一个面都是边长为4的正三角形,且顶点在同一个平面内.若点在四边形内(包含边界)运动,为的中点,则( )
 A、当为的中点时,异面直线与所成角为 B、当平面时,点的轨迹长度为 C、当时,点到的距离可能为 D、存在一个体积为的圆柱体可整体放入内
A、当为的中点时,异面直线与所成角为 B、当平面时,点的轨迹长度为 C、当时,点到的距离可能为 D、存在一个体积为的圆柱体可整体放入内 -
11、如图,在中, , D在边AB上, , , 则( )
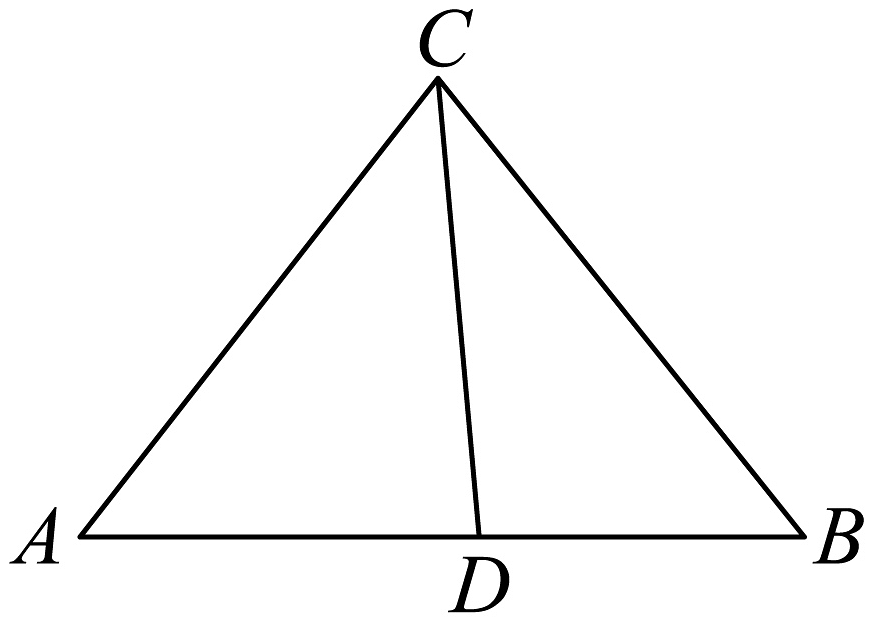 A、 B、 C、 D、
A、 B、 C、 D、 -
12、已知 , 若方程有三个不同的实数解,则实数的取值范围为 .
-
13、定义 , 设 , 则下列结论不正确的是( )A、 B、不等式的解集为 C、当时,的最大值为 D、在上单调递减
-
14、已知函数 , 则下列结论正确的是( )A、函数的定义域为 B、函数的值域为 C、 D、函数为减函数
-
15、如图,我国南海某处的一个圆形海域上有四个小岛,小岛与小岛、小岛 相距都为 , 与小岛相距为 . 小岛对小岛与的视角为钝角,且 .

(Ⅰ)求小岛与小岛之间的距离和四个小岛所形成的四边形的面积;
(Ⅱ)记小岛对小岛与的视角为 , 小岛对小岛与的视角为 , 求的值.
-
16、如图,在四棱锥中,平面 , 底面是菱形, . 点 , 分别在棱 , 的中点.

(1)证明:平面 .
(2)若 , 求点到平面的距离.
-
17、在① , ②这两个条件中任选一个,补充在下面问题中,并求解(1)、(2)的答案.问题:在中,三个内角A,B,C所对的边分别是a,b,c,已知________.(1)、求角C;(2)、若 , 的面积 , 求的周长.
(注:如果选择两个条件分别解答,则按第一个解答计分.)
-
18、已知向量与的夹角 , 且 , .(1)、求;(2)、在上的投影向量;(3)、求向量与夹角的余弦值.
-
19、已知球是圆锥的外接球,圆锥的母线长是底面半径的倍,且球的表面积为 , 则圆锥的侧面积为.
-
20、函数的最大值为.