相关试卷
- 河北省张家口市2016-2017学年高一下学期数学期末考试试卷
- 河北省邢台市2016-2017学年高一下学期数学期末考试试卷
- 河北省唐山市2016-2017学年高一下学期数学期末考试试卷
- 河北省廊坊市省级示范高中联合体2016-2017学年高一下学期数学期末考试试卷
- 河北省衡水市深州中学2016-2017学年高一下学期数学期末考试试卷
- 河北省邯郸市2016-2017学年高一下学期数学期末考试试卷
- 河北省承德市2016-2017学年高一下学期数学期末考试试卷
- 河北省保定市2016-2017学年高一下学期数学期末考试试卷
- 江西省赣州市2016-2017学年高一下学期期末数学考试试卷
- 四川省雅安市2016-2017学年高二下学期数学期末考试试卷(文科)
-
1、如图1,已知直角梯形AEFD中, , 点B,C分别在AE,DF上,且 , , , , 将图1沿BC翻折,使平面平面BEFC得图2.
 (1)、在线段CF上是否存在一点M,使得A、E、M、D四点共面.若存在,请给出证明;若不存在,请说明理由;(2)、当时,求平面AEF与平面CEF的夹角的正切值.
(1)、在线段CF上是否存在一点M,使得A、E、M、D四点共面.若存在,请给出证明;若不存在,请说明理由;(2)、当时,求平面AEF与平面CEF的夹角的正切值. -
2、已知函数 .(1)、求函数的单调递增区间;(2)、若函数在区间上的最大值为2,求t的取值范围.
-
3、某省采用“3+1+2”新高考模式,其中“3”为语文、数学和外语3门全国统考科目;“1”为考生在物理和历史中选择1门;“2”为考生在思想政治、地理、化学和生物4门中再选择2门.为了研究高一年级学生的选科类别是否与选生物有关联,在某中学高一年级的所有学生中随机抽取200人进行调查,整理得到如下列联表:
选科类别
是否选择生物
合计
选择生物
不选择生物
物理类
100
60
160
历史类
15
25
40
合计
115
85
200
(1)、依据小概率值的独立性检验,能否认为选科类别与选择生物有关联?(2)、现从选物理类的样本中,按分层随机抽样的方法选出8人组成一个小组,从抽取的8人中再随机抽取3人参加生物竞赛,求这3人中,选择生物的人数的分布列和数学期望.附: .
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
-
4、已知抛物线的焦点为 , 准线与轴的交点为 , 点在上,且 , 则的面积为 .
-
5、如图,在长方体中, , 则直线与平面所成角的正弦值为 .

-
6、数据: , , , , , , , , , 的第百分位数为 .
-
7、函数的图象关于坐标原点成中心对称图形的充要条件是函数为奇函数,我们发现可以推广为:函数的图象关于点成中心对称图形的充要条件是函数为奇函数,下列说法正确的是( )A、的对称中心为 B、的对称中心为 C、类比上面推广结论:函数的图象关于直线成轴对称图形的充要条件是函数为偶函数 D、类比上面推广结论:函数的图象关于直线成轴对称图形的充要条件是函数为偶函数
-
8、设复数是虚数,复数是实数,则下列说法正确的是( )A、的值为1 B、的实部的取值范围为 C、为纯虚数 D、的最小值为2
-
9、已知命题p: , , 命题q: , , 则( )A、和q都是真命题 B、p和q都是假命题 C、p和都是假命题 D、和都是真命题
-
10、一个盒子中装有4个黑球和6个白球,每个球编有不同的号码,现从中任取2个球,已知一个球是白球,则另一个球也是白球的概率为( )A、 B、 C、 D、
-
11、若平面内三点O,M,N满足 , , , 则的值为( )A、2 B、1 C、 D、
-
12、设椭圆的左、右焦点分别为 , , 点在上, , 且椭圆过点 , 则椭圆的离心率为( )A、 B、 C、 D、
-
13、函数在一个周期内的图象如图所示,则函数的一个对称中心为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、已知等比数列的各项均为正数,若 , 则等于( )A、1 B、2 C、3 D、4
-
15、已知 , , , 则a,b,c的大小关系为( )A、 B、 C、 D、
-
16、点到直线l:的距离为( )A、 B、 C、 D、
-
17、已知向量 , , 若与共线,则t的值为( )A、25 B、-25 C、-4 D、4
-
18、已知平面平面 , 且均与球相交,得截面圆与截面圆为线段的中点,且 , 线段与分别为圆与圆的直径,则( )A、若为等边三角形,则球的体积为 B、若为圆上的中点, , 且 , 则与所成角的余弦值为 C、若 , 且 , 则 D、若 , 且与所成的角为 , 则球的表面积为或
-
19、某校为了解本校学生每天的体育活动时间,随机抽取了100名学生作为样本,统计并绘制了如下的频率分布直方图:
 (1)、从这100名学生中按照分层抽样的方式在体育活动时间位于和的两组学生中抽取12名学生,再从这12名学生中随机抽取3人,用表示这3人中属于的人数,求的分布列和数学期望;(2)、以这100名学生体育活动时间的频率估计该校学生体育活动时间的概率,若从该校学生中随机抽取且名学生,求证:当时,“抽取的名学生中恰有5人每天的体育活动时间不低于40分钟”的概率最大.
(1)、从这100名学生中按照分层抽样的方式在体育活动时间位于和的两组学生中抽取12名学生,再从这12名学生中随机抽取3人,用表示这3人中属于的人数,求的分布列和数学期望;(2)、以这100名学生体育活动时间的频率估计该校学生体育活动时间的概率,若从该校学生中随机抽取且名学生,求证:当时,“抽取的名学生中恰有5人每天的体育活动时间不低于40分钟”的概率最大. -
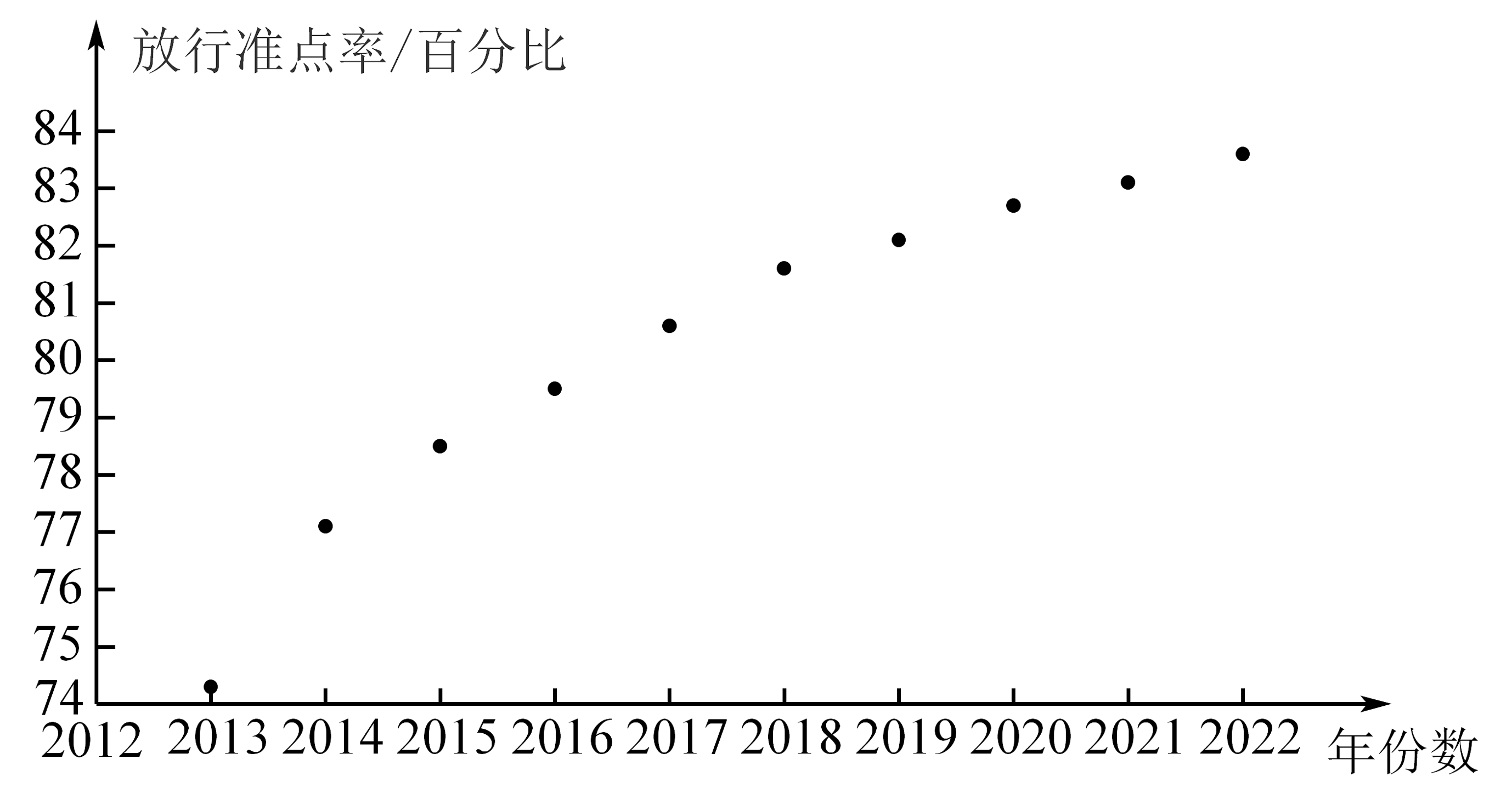
20、放行准点率是衡量机场运行效率和服务质量的重要指标之一.某机场自2012年起采取相关策略优化各个服务环节,运行效率不断提升.以下是根据近10年年份数与该机场飞往A地航班放行准点率()(单位:百分比)的统计数据所作的散点图及经过初步处理后得到的一些统计量的值.
2017.5
80.4
1.5
40703145.0
1621254.2
27.7
1226.8
其中 , .
(1)、根据散点图判断,与哪一个适宜作为该机场飞往A地航班放行准点率y关于年份数x的经验回归方程类型(给出判断即可,不必说明理由),并根据表中数据建立经验回归方程,由此预测2023年该机场飞往A地的航班放行准点率;(2)、已知2023年该机场飞往A地、B地和其他地区的航班比例分别为0.2、0.2和0.6.若以(1)中的预测值作为2023年该机场飞往A地航班放行准点率的估计值,且2023年该机场飞往B地及其他地区(不包含A、B两地)航班放行准点率的估计值分别为和 , 试解决以下问题:(i)现从2023年在该机场起飞的航班中随机抽取一个,求该航班准点放行的概率;
(ii)若2023年某航班在该机场准点放行,判断该航班飞往A地的概率.(保留3位小数)
附:对于一组数据 , , …, , 其回归直线的斜率和截距的最小二乘估计分别为 ,
参考数据: , , .