版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、在平面直角坐标系 $x O y$ 中，已知圆 $C : {(x - 1)}^{2} + {(y - 2)}^{2} = r^{2} (r > 0)$ ，点 $A (4, 0)$ ，若圆 $C$ 上存在点 $M$ ，满足 $| M A |^{2} + | M O |^{2} = 10$ ，则 $r$ 的取值范围是（）

A、 $(0, \sqrt{5} + 1]$ B、 $[\sqrt{5} - 1, \sqrt{5} + 1]$ C、 $(0, \sqrt{5} - 1]$ D、 $[\sqrt{5} + 1, + \infty)$

查看解析
2、已知正项等差数列 $\{a_{n}\}$ 满足 $\frac{a_{1} + a_{3} + \dots + a_{2 n - 1}}{a_{3} + a_{5} + \dots + a_{2 n + 1}} = \frac{n}{n + 2} (n \in N^{*})$ ，则 $\frac{a_{4050}}{a_{2}} =$ （）

A、4050 B、2025 C、4048 D、2024

查看解析
3、已知 $|z - 1| = |z - i| (z \neq 0)$ ，则在复平面内 $\frac{\bar{z} + z}{z}$ 所对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看解析
4、 ${(x + \frac{1}{x})}^{6}$ 的展开式中系数最大的项为（）

A、第3项 B、第4项 C、第5项 D、第6项

查看解析
5、已知平面向量 $|\vec{a}| = |\vec{b}| = 1$ 且 $\vec{a} \cdot \vec{b} = 0$ ，两个非零向量 $\vec{m} = x \vec{a} + \vec{b}, \vec{n} = (3 x - 2) \vec{a} - \vec{b}$ ，若 $\vec{m} ⊥ \vec{n}$ ，则实数 $x$ 的值为（）

A、1 B、 $- \frac{1}{3}$ C、1或 $- \frac{1}{3}$ D、 $- 1$ 或 $\frac{1}{3}$

查看解析
6、已知集合 $A = \{x ∣ x + 1 \leq 0\}$ ， $B = \{x ∣ x^{2} + x - 2 < 0\}$ ，则 $A \cup B =$ （）

A、 ${x ∣ x < 1}$ B、 ${x ∣ - 2 < x < 1}$ C、 $\{x ∣ x > - 2\}$ D、 ${x ∣ - 2 < x \leq - 1}$

查看解析
7、为激发户外运动爱好者健身热情，增进群众健身获得感、幸福感. 某市体育部门随机抽取200名群众进行每天体育运动时间的调查，按照时长(单位：分钟)分成6组：[30，40)，[40，50)，[50，60)，[60，70)，[70，80)，[80，90]. 处理后绘制了如下图的频率分布直方图.

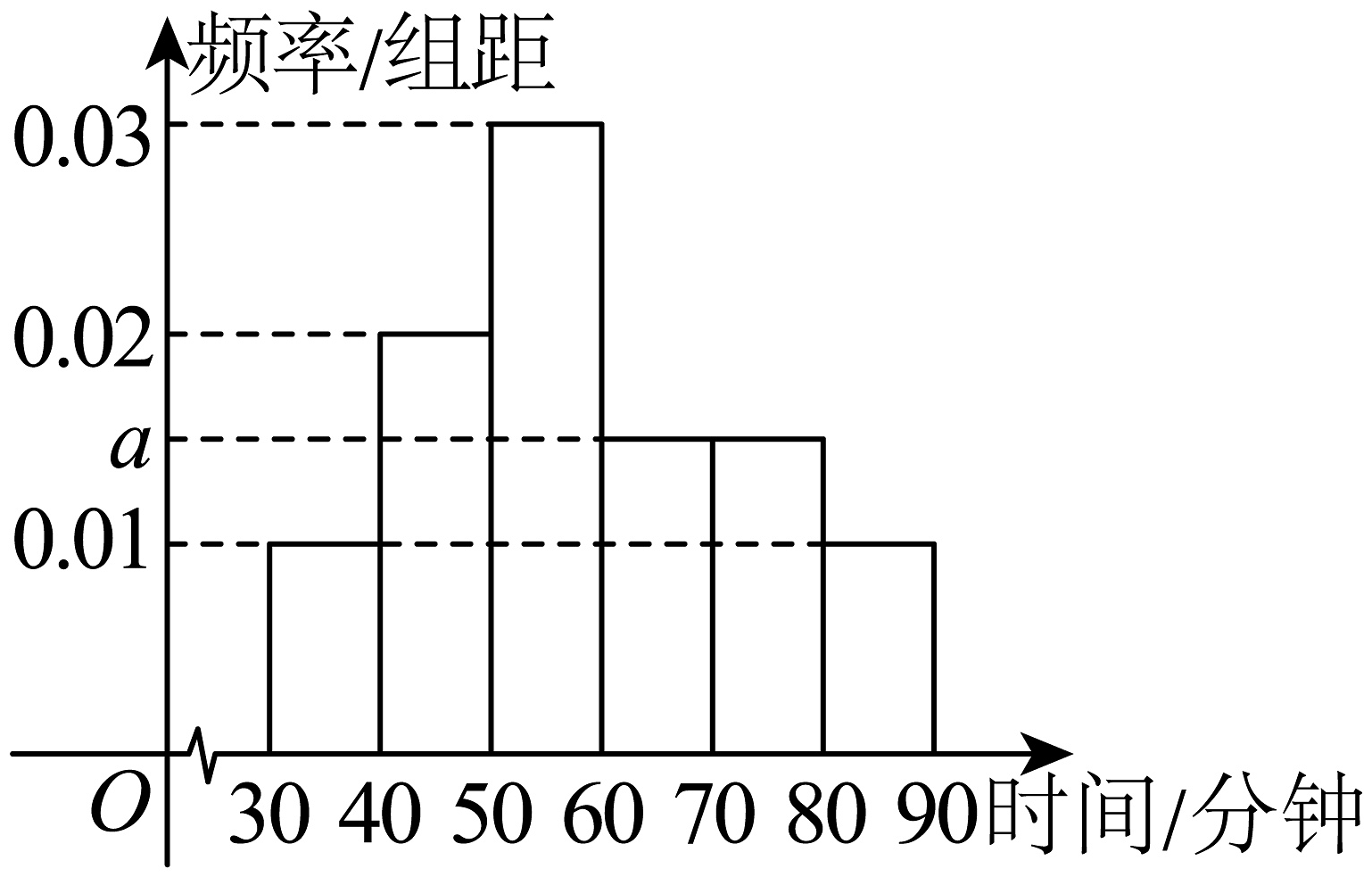(1)、求图中 $a$ 的值；

(2)、求运动时长在[50，70)的样本群众人数；

(3)、估计该市群众每天体育运动时间的众数、平均数、中位数(保留1位小数).

查看解析
8、如图所示，已知多面体PABCDE的底面ABCD是边长为2的菱形，点F是PC的中点，AC交BD于点O，PA $⊥$ 底面ABCD，ED $/ /$ PA，且 $P A = 2 E D = 2$ .

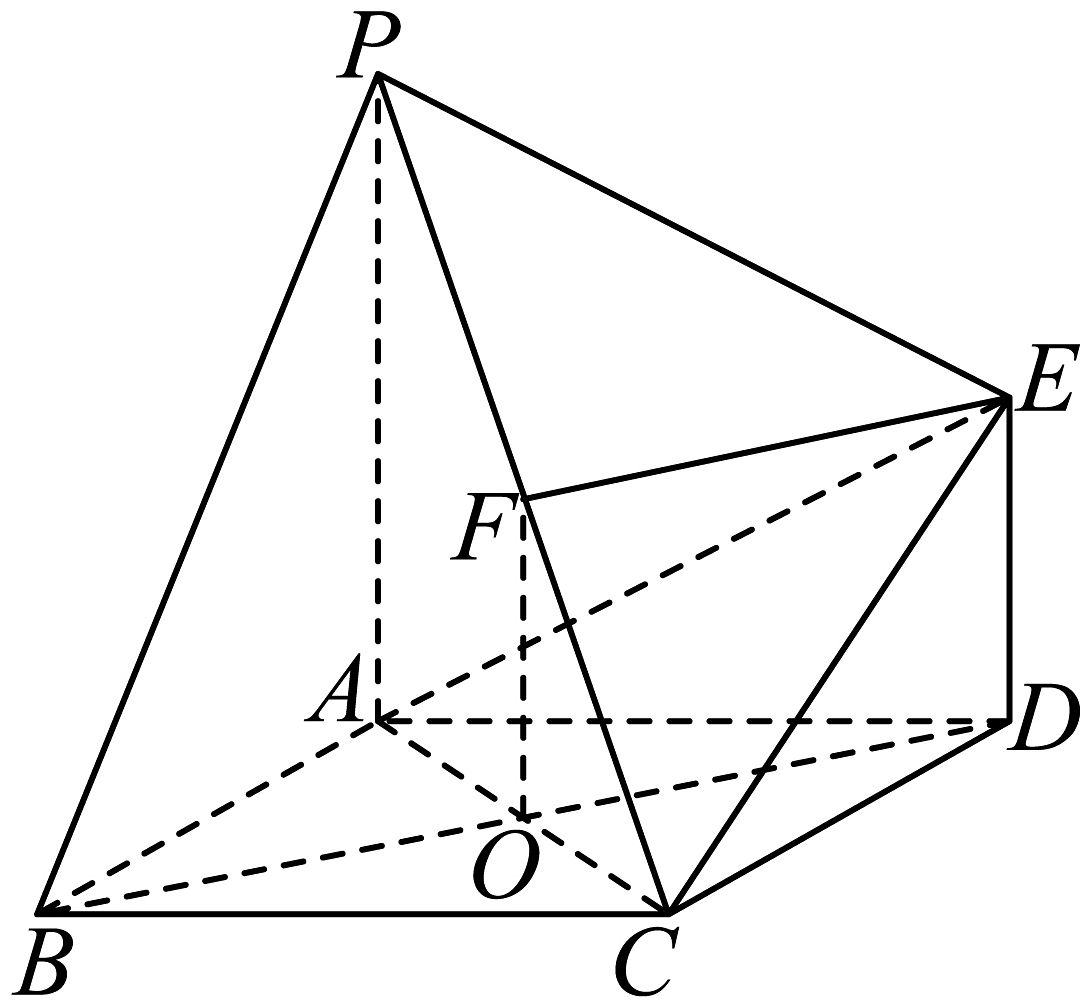(1)、证明：OF $/ /$ 平面PAB ；

(2)、证明：BD $⊥$ 平面PAC ；

(3)、若 $∠ A B C = 60 °$ ，求三棱锥 $E - P A C$ 的体积.

查看解析
9、已知在等差数列 $\{a_{n}\}$ 中， $a_{2} = 3$ ， $a_{4} + a_{6} = 18$ .

(1)、求数列 $\{a_{n}\}$ 通项公式；

(2)、设 $b_{n} = \frac{2}{n (a_{n} + 3)}$ ，求数列 $\{b_{n}\}$ 的前 $n$ 项和 $S_{n}$ .

查看解析
10、在 $△ A B C$ 中，角 $A$ 、 $B$ 、 $C$ 所对的边为 $a$ 、 $b$ 、 $c$ ，已知 $a^{2} + c^{2} - b^{2} = a c$ .

(1)、求角 $B$ 的值；

(2)、若 $b = \sqrt{6}$ ， $△ A B C$ 的面积为 $\frac{5 \sqrt{3}}{2}$ ，求 $△ A B C$ 的周长.

查看解析
11、（1）求函数 $f (x) = \frac{l n (x^{2} + 3 x - 18)}{\sqrt{x - 5}}$ 的定义域；
（2）已知直线 $\frac{x}{a} + \frac{y}{b} = 1$ $(a > 0, b > 0)$ 过点 $(2, 1)$ ，求 $a + 2 b$ 的最小值.

查看解析
12、已知 $f (x)$ 为定义在 $R$ 上的奇函数，当 $x < 0$ 时， $f (x) = 2 x - {(\frac{1}{3})}^{x}$ ，则 $f (2) =$ .

查看解析
13、已知函数 $f (x) = \{\begin{matrix} f (x + 2), x < 3 \\ 2^{x} - 1, x \geq 3 \end{matrix}$ ，则 $f (- 1)$ =

查看解析
14、已知集合 $A = {1, 6}$ ， $B = {1, 2 m, m^{2} - m}$ ，且 $A \subseteq B$ ，则实数 $m$ 的值为．

查看解析
15、已知 $α, β$ 为两个平面， $m, n$ 为两条直线，则下列命题正确的是（）

A、若 $m // α ， n ⊥ α$ ，则 $m ⊥ n$ B、若 $m // α ， n // α$ ，则 $m / / n$ C、若 $m ⊥ α ， m \subset β$ ，则 $α ⊥ β$ D、若 $m ⊥ α ， m ⊥ β$ ，则 $α // β$

查看解析
16、已知 $\vec{a}$ 和 $\vec{b}$ 为单位向量，且 $|\vec{a} - 3 \vec{b}| = \sqrt{10}$ ，则下列说法正确的是（）

A、 $\vec{a} ⊥ \vec{b}$ B、 $\vec{a} \cdot (2 \vec{a} - \vec{b}) = 2$ C、 $\vec{a}$ 与 $\vec{b}$ 的夹角为 $60^{\circ}$ D、 $\vec{a} + \vec{b}$ 在 $\vec{b}$ 方向上的投影向量是 $\vec{b}$

查看解析
17、已知复数 $z$ 在复平面对应的点为 $A$ ，且 $\frac{z}{z + 1} = 2 + i^{3}$ ，则下列说法正确的是（）

A、 $\bar{z} = \frac{3}{2} + \frac{1}{2} i$ B、 $|z| = \frac{\sqrt{10}}{2}$ C、 $z$ 的虚部为 $- \frac{1}{2} i$ D、 $A (- \frac{3}{2}, - \frac{1}{2})$

查看解析
18、已知 $a = {0.6}^{0.5}$ ， $b = {0.6}^{0.3}$ ， $c = \log_{0.6} 0.3$ ，则 $a$ 、 $b$ 、 $c$ 的大小关系是（）

A、 $c > b > a$ B、 $c > a > b$ C、 $b > c > a$ D、 $a > b > c$

查看解析
19、下列函数中，既是偶函数，又在 $(- \infty, 0)$ 上单调递增的函数是（）

A、 $y = x^{3}$ B、 $y = {(\frac{1}{3})}^{|x|}$ C、 $y = \frac{1}{x}$ D、 $y = x^{2} + 1$

查看解析
20、已知向量 $\vec{a} = (1, - 1)$ ， $\vec{b} = (3, m)$ ， $\vec{a} ⊥ (\vec{b} - 2 \vec{a})$ ，则实数 $m =$ （）

A、 $- 2$ B、 $- 1$ C、 $0$ D、 $2$

查看解析

上一页 433 434 435 436 437 下一页跳转