相关试卷
- 河北省张家口市2016-2017学年高一下学期数学期末考试试卷
- 河北省邢台市2016-2017学年高一下学期数学期末考试试卷
- 河北省唐山市2016-2017学年高一下学期数学期末考试试卷
- 河北省廊坊市省级示范高中联合体2016-2017学年高一下学期数学期末考试试卷
- 河北省衡水市深州中学2016-2017学年高一下学期数学期末考试试卷
- 河北省邯郸市2016-2017学年高一下学期数学期末考试试卷
- 河北省承德市2016-2017学年高一下学期数学期末考试试卷
- 河北省保定市2016-2017学年高一下学期数学期末考试试卷
- 江西省赣州市2016-2017学年高一下学期期末数学考试试卷
- 四川省雅安市2016-2017学年高二下学期数学期末考试试卷(文科)
-
1、已知函数的部分图象如图所示,则的单调递增区间为( )
 A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 , -
2、设直线与圆交于A,B两点,则的取值范围为( )A、 B、 C、 D、
-
3、展开式中的常数项为( )A、 B、 C、 D、
-
4、某药厂为获得新研发药品的治愈率 , 委托某公司进行调查,首轮抽取个患者进行试验,每个患者是否治愈相互独立.(1)、假设 , 回答以下问题:
(ⅰ)若 , 求患者痊愈比例为到的概率.
(ⅱ)该公司第二轮再抽取个患者进行试验.为简化运算过程,拟用计算两轮试验治愈总人数为的概率,是否合理?若合理,请证明;若不合理,请说明理由.
(2)、在重伯努利试验中,随机变量 , 随着试验次数增加,其概率计算较为复杂,此时,根据中心极限定理,近似服从正态分布 , 故常用以下公式简化概率计算: , 其中 , 随机变量 . 若用该公司首轮试验的治愈频率来估计治愈率 , 为保证有把握,使得与之间误差不超过0.01,则至少应抽取多少个患者?参考数据: .
-
5、对于数列 , 若 , 使得 , 都有成立,则称为“三和定值数列”.已知为“三和定值数列”,且 , , .(1)、求 , , ;(2)、已知为数列的前项和,求 .
-
6、如图,为圆锥的顶点,是圆锥底面的圆心,为底面直径,为圆锥底面圆周上异于的一点,为上一点,且平面 .
 (1)、求的值;(2)、设 , 二面角的正切值为 , 求直线与平面所成角的大小.
(1)、求的值;(2)、设 , 二面角的正切值为 , 求直线与平面所成角的大小. -
7、某校元旦晚会设计了一个抽奖游戏,主持人从编号为四个外观相同的空箱子中随机选择一个,放入奖品,再将四个箱子关闭,即主持人知道奖品在哪个箱子.当抽奖人选择某个箱子后,在箱子打开之前,主持人会随机打开一个没有奖品的箱子,并问抽奖人是否愿意更改选择以便增加中奖概率.已知甲先选择了号箱子,此时主持人打开号箱子的概率为 , 在主持人打开号箱子的情况下,奖品在号箱子的概率为 .
-
8、准线方程为的抛物线的标准方程为.
-
9、数学中有许多形状优美、寓意美好的曲线,曲线就是其中之一,如图所示 . 已知点是上一点,则( )
 A、 B、 C、当时,的最大值为 D、曲线在轴左侧所围成的区域面积大于2
A、 B、 C、当时,的最大值为 D、曲线在轴左侧所围成的区域面积大于2 -
10、已知函数 , 则( )A、的图象关于点对称 B、的图象关于直线对称 C、在上单调递减 D、直线是曲线的一条切线
-
11、某次跳水比赛的计分规则如下:共有7个裁判打分,去掉一个最高分与一个最低分后,取剩余5个分数的平均值,比较前、后两组数据的数字特征,则( )A、中位数不变 B、极差不变 C、平均数大小关系不确定 D、方差变小
-
12、已知是双曲线的左、右焦点,为双曲线上的两点,若 , 且以为直径的圆恰好过点 , 则双曲线的离心率为( )A、 B、 C、 D、
-
13、如图,将绘有函数部分图像的纸片沿轴折成直二面角,此时之间的距离为 , 则( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、设函数 , , 曲线和恰有一个交点,则( )A、 B、 C、 D、
-
15、已知的内角的对边分别为 , 在方向上的投影向量为 , 则( )A、 B、 C、 D、
-
16、已知平面 , 和直线 , , , 则“”是“”的( )A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件
-
17、图中阴影部分用集合符号可以表示为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、复数在复平面内对应的点位于A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
19、若 , 则下列关系正确的是( ).A、 B、 C、 D、
-
20、函数的图象如图所示,则下列说法正确的是( )
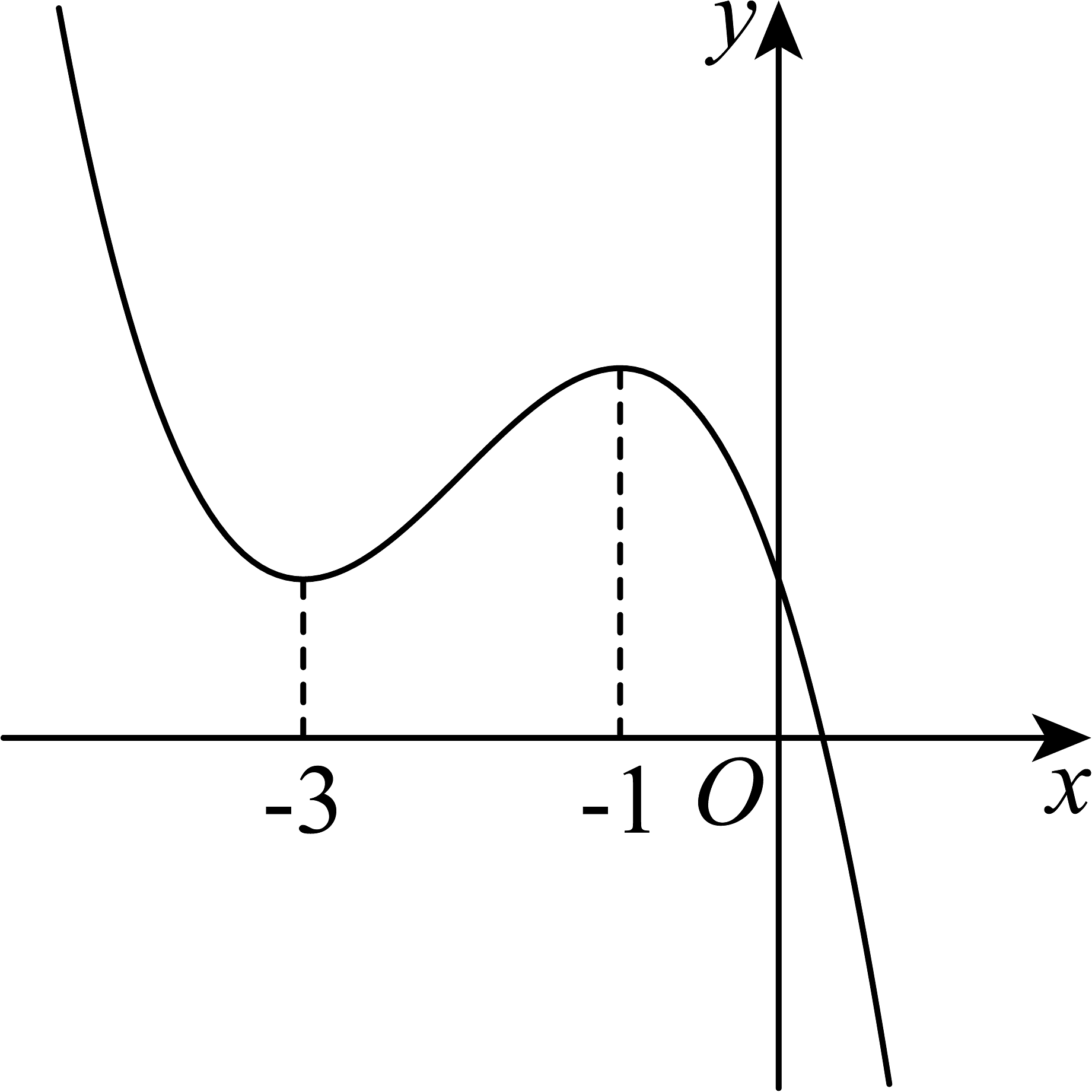 A、 , B、若方程有3个不同的实数根,则 C、直线是曲线的切线 D、点是曲线的对称中心
A、 , B、若方程有3个不同的实数根,则 C、直线是曲线的切线 D、点是曲线的对称中心