相关试卷
- 河北省张家口市2016-2017学年高一下学期数学期末考试试卷
- 河北省邢台市2016-2017学年高一下学期数学期末考试试卷
- 河北省唐山市2016-2017学年高一下学期数学期末考试试卷
- 河北省廊坊市省级示范高中联合体2016-2017学年高一下学期数学期末考试试卷
- 河北省衡水市深州中学2016-2017学年高一下学期数学期末考试试卷
- 河北省邯郸市2016-2017学年高一下学期数学期末考试试卷
- 河北省承德市2016-2017学年高一下学期数学期末考试试卷
- 河北省保定市2016-2017学年高一下学期数学期末考试试卷
- 江西省赣州市2016-2017学年高一下学期期末数学考试试卷
- 四川省雅安市2016-2017学年高二下学期数学期末考试试卷(文科)
-
1、在数列中, , 若 , 则;
-
2、如图,已知正四棱台的上、下底面边长分别为2和4,侧棱长为 , 点为棱的中点,点在侧面内运动(包含边界),且与平面所成角的正切值为 , 则( )
 A、长度的最小值为 B、存在点 , 使得 C、存在点 , 使得 D、棱长为1.5的正方体可以在此空心棱台容器内部任意转动
A、长度的最小值为 B、存在点 , 使得 C、存在点 , 使得 D、棱长为1.5的正方体可以在此空心棱台容器内部任意转动 -
3、已知函数的图象过点 , 下列说法中正确的有( )A、若 , 则在上单调递减 B、若把的图象向左平移个单位后得到的函数为偶函数,则的最小值为2 C、若在上有且仅有4个零点,则 D、若 , 且在区间上有最小值无最大值,则
-
4、下面命题为假命题的是( )A、若 , , 则 B、函数的单调减区间是 C、的最小值是 D、与是同一函数
-
5、已知函数有三个零点,则t的取值范围是( )A、 B、 C、 D、
-
6、牛顿冷却定律描述一个事物在常温环境下的温度变化:如果物体的初始温度为 , 则经过一定时间t(单位:分钟)后的温度T满足 , 其中是环境温度,h称为半衰期,现有一杯80℃的热水用来泡茶,研究表明,此茶的最佳饮用口感会出现在55℃.经测量室温为25℃,茶水降至75℃大约用时1分钟,那么为了获得最佳饮用口感,从降至75℃开始大约还需要等待( )(参考数据: , , )A、3分钟 B、5分钟 C、7分钟 D、9分钟
-
7、在数列中, , , 则的通项公式为( )A、 B、 C、 D、
-
8、下列四个图象可能是函数图象的是( )A、
 B、
B、 C、
C、 D、
D、
-
9、已知命题 , 则为( )A、 B、 C、 D、
-
10、已知复数 , 则( )A、 B、 C、 D、
-
11、设集合 , 集合 .(1)、若 , 求和(2)、设命题 , 命题 , 若是成立的必要不充分条件,求实数的取值范围.
-
12、已知集合 , 若 , 则实数
-
13、如图,在四棱锥中,平面平面 , 且 .
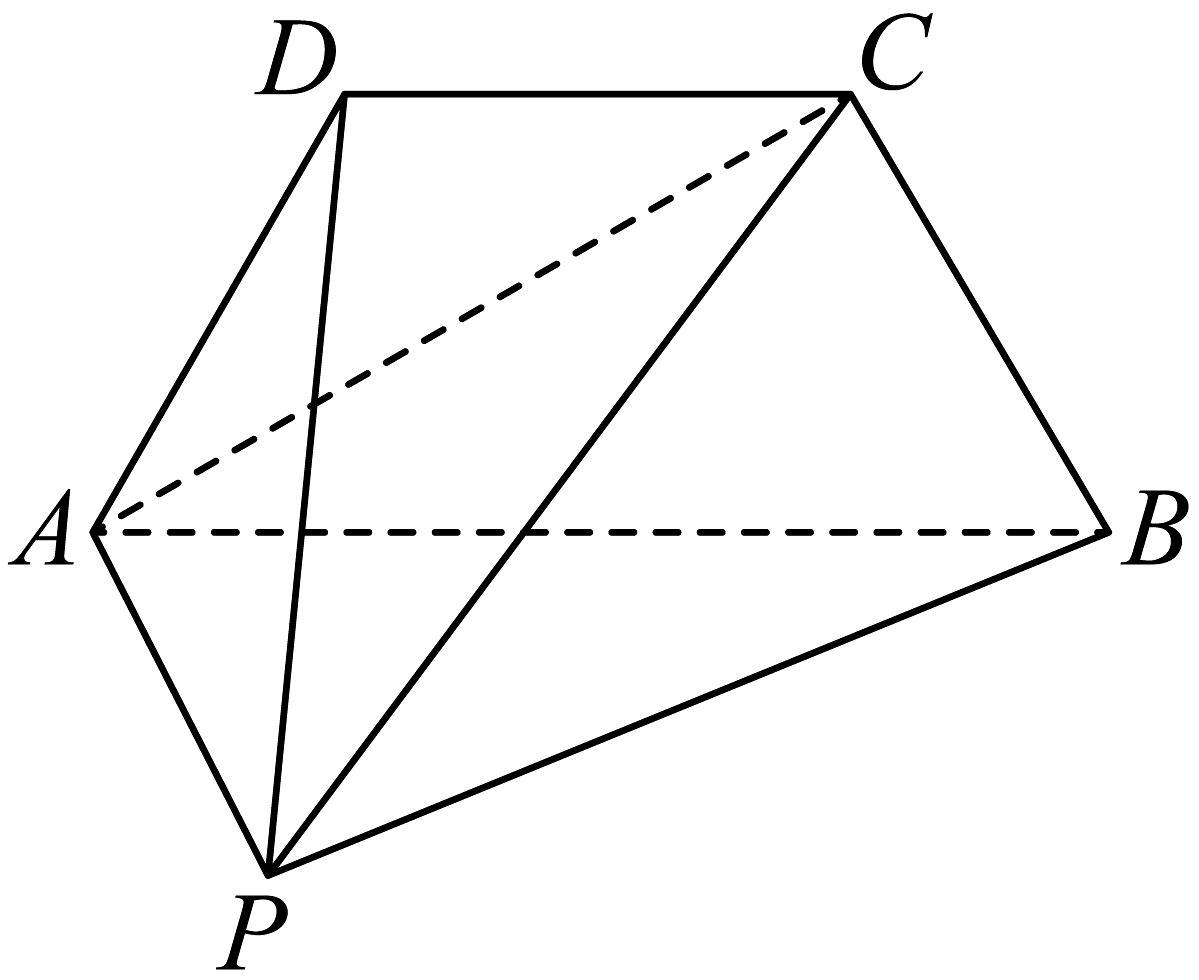 (1)、证明:平面平面;(2)、求平面与平面夹角的正弦值.
(1)、证明:平面平面;(2)、求平面与平面夹角的正弦值. -
14、已知函数 , 若 , 都有成立,则的取值范围为( )A、 B、 C、 D、
-
15、下列说法正确的是( )A、“”是“直线与直线互相垂直”的充要条件 B、“”是“直线与直线互相平行”的充要条件 C、直线的倾斜角的取值范围是 D、若点 , , 直线过点且与线段相交,则的斜率的取值范围是
-
16、正实数 , 满足 , 则的最小值为 .
-
17、甲同学现参加一项答题活动,其每轮答题答对的概率均为 , 且每轮答题结果相互独立.若每轮答题答对得5分,答错得0分,记第轮答题后甲同学的总得分为 , 其中.(1)、求;(2)、若乙同学也参加该答题活动,其每轮答题答对的概率均为 , 并选择另一种答题方式答题:从第1轮答题开始,若本轮答对,则得20分,并继续答题;若本轮答错,则得0分,并终止答题,记乙同学的总得分为.证明:当时,.
-
18、某同学喜爱篮球和跑步运动.在暑假期间,该同学下午去打篮球的概率为.若该同学下午去打篮球,则晚上一定去跑步;若下午不去打篮球,则晚上去跑步的概率为.已知该同学在某天晚上去跑步,则下午打过篮球的概率为.
-
19、已知 , , , 则 .
-
20、已知的定义域为为奇函数,为偶函数,若当时, , 则( )A、 B、0 C、1 D、e