-
1、观察下面的等式:
第 1 个等式: ,
第 2 个等式: ,
第 3 个等式: ,
第 4 个等式: ,
……
按照以上规律,解决下列问题:
(1)、写出第 5 个等式:;(2)、请你猜想第 n 个等式(用含 n 的式子表示),并证明. -
2、如图,平行四边形ABCD中,AE平分∠BAD交BC于点E.
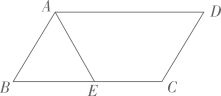 (1)、尺规作图:作CF平分∠BCD交AD于点F(不写作法,保留作图痕迹);(2)、求证:四边形AECF是平行四边形.
(1)、尺规作图:作CF平分∠BCD交AD于点F(不写作法,保留作图痕迹);(2)、求证:四边形AECF是平行四边形. -
3、佳佳计算分式方程 的过程如下:
解方程:
去分母,得 第①步
移项,得 第②步
合并同类项,得 第③步
系数化1,得 第④步
经检验, 是该分式方程的解.
(1)、佳佳在计算过程中,第一次出现错误的步骤是(填序号);(2)、请你写出正确的解答过程. -
4、(1)、计算:;(2)、解方程:.
-
5、 已知二次函数y=ax2+2ax+d(a<0)的图象上有两点 , , 当 时, 始终有 , 则 m 的取值范围是.
-
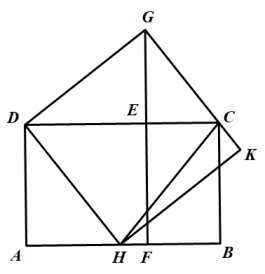
6、“化积为方”是一个古老的几何学问题,即给定一个长方形,作一个和它面积相等的正方形,这也是证明勾股定理的一种思想方法,如图所示,在矩形ABCD中(AB>AD),以AD为边作正方形ADEF,在FE的延长线上取一点G,使得∠DGC=RT∠,过点D作DH⊥DG交AB于点H,过点H作HK⊥GC于点K.若AF=2,BF=3FH,则FH的长为.
-
7、如图,AB是半圆O的直径,点C在半圆上,CD是半圆的切线,cosD= , ∠CAB=30° .若CD=6,则AC的长是.

-
8、已知分式 , 若当x=1时分式的值为0,则实数α的值为.
-
9、一个不透明的袋子中,有5个除颜色外完全相同的小球,其中3个红球,2个白球,随机摸出一个小球,摸出红球的概率是.
-
10、 如图,在四边形 ABCD 中, , 对角线 AC 和 BD 交于点 E,若 , , 则 BD 长的最小值为( )
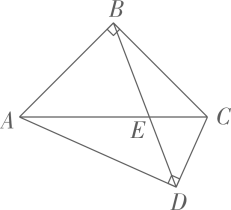 A、6 B、 C、4 D、
A、6 B、 C、4 D、 -
11、 如图,一次函数 的图象与反比例函数 的图象相交于第一象限内的两点 A(m,3n),B(m+2,n),且直线 与 x 轴交于点 C,则下列结论中正确的是( )
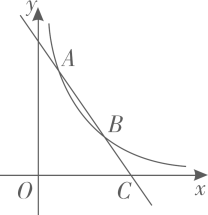 A、 B、 C、 D、当 时,
A、 B、 C、 D、当 时, -
12、已知一个菱形的周长是20,面积是24,则该菱形的两条对角线的长度之和为( )A、7 B、4 C、14 D、8
-
13、 不等式组的解集在数轴上可表示为( )A、
 B、
B、 C、
C、 D、
D、
-
14、 如图,在平面直角坐标系xOy中,△ABC和△A'B'C位似,位似中心为原点O.已知点A(-1,1.5),点A'(2,-3),若△ABC的面积为2,则△A'B'C'的面积是( )
 A、2 B、4 C、8 D、16
A、2 B、4 C、8 D、16 -
15、一次空气污染指数抽查中,收集到某地一周的数据如下:67,68,63,90,89,75,89.该组数据的中位数是( )A、68 B、75 C、89 D、90
-
16、 下列式子运算正确的是( )A、 B、 C、 D、
-
17、 截止2025年4月9日,《哪吒之魔童闹海》全球票房(含预售及海外)已破1560000000元. 其中数“15600000000”用科学记数法表示为( )A、 B、 C、 D、
-
18、6个相同正方体搭成的几何体俯视图为( )
 A、
A、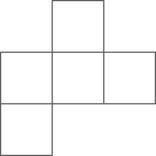 B、
B、 C、
C、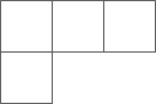 D、
D、
-
19、以下四个城市中某天上午9时气温最低的城市是( )
杭州
温州
宁波
嘉兴
-2℃
0℃
1℃
-1℃
A、杭州 B、温州 C、宁波 D、嘉兴 -
20、综合与实践
【新知定义】在平面内,两个面积相等的三角形,若有公共顶点,且公共顶点所在的角相等,则称这两个三角形关于这个顶点成“友谊三角形”.例如:如图1,在△ABC和△ADE中,若∠BAC=∠DAE,S△ABC=S△ADE , 则△ABC和△ADE关于点A成“友谊三角形”.
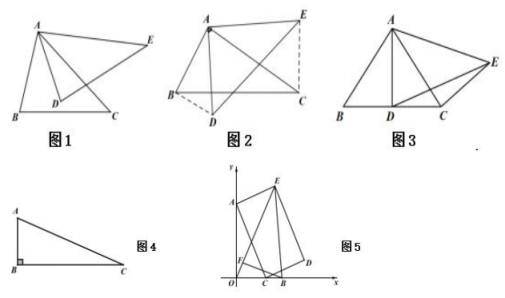 (1)、【特例初探】数学社团的小智同学发现:如图2,∠BAC=∠DAE=90°,S△ABC=S△ADE , 连接BD、CE,可得到△BAD∽△EAC.理由如下:
(1)、【特例初探】数学社团的小智同学发现:如图2,∠BAC=∠DAE=90°,S△ABC=S△ADE , 连接BD、CE,可得到△BAD∽△EAC.理由如下:即:① ▲
∵
∴② ▲
又
.
根据小智的思路,请完成填空:①②
(2)、【变式归纳】小慧思考:如果∠BAC=∠DAE≠90°,△BAD∽△EAC是否还成立?于是她作了进一步探究:如图3,在△ABC中,AB=AC=5,BC=6,AD⊥BC,△ADE和△ABC关于点A成“友谊三角形”,连接CE,请你完成以下问题:①AE= ▲ ;
②试判断AC与CE的位置关系,并说明理由;
(3)、【迁移应用】如图4,在△ABC中,∠B=90°,点P是BC边上一点,请你借助以上结论或方法,用无刻度直尺和圆规在图4中作△APQ,使△APQ和△ABC关于点A成“友谊三角形”,且AQ=AC;(4)、【综合提升】如图5,在平面直角坐标系中,已知A(0,3)、B(2,0).C是x轴上的一动点,以AC为一边在AC的右侧构造矩形ACDE,且矩形的面积始终是6,连接OE、BE.F是线段OE上一点,且满足∠OFB+∠AOE=∠OEB+90°,连接BF,则BF·OE的最小值为.