-
1、 一项工程,甲队单独施工需要a天完成,乙队单独施工需要b天完成,丙队单独施工需要c天完成,若甲、乙、丙三队同时施工则只需要2天可完成,已知a,b,c均为正整数.(1)、求a,b,c满足的等量关系;(2)、若甲、乙两队同时施工4天后,剩余的工程由丙队单独施工,则丙队还需1天可以完成该项工程,求c的值;(3)、若 , 求乙、丙两队同时施工需要多久可以完成该项工程.
-
2、 如图,已知 , F,E分别为 , 上的点,的角平分线交于点G, , 垂足为H,的角平分线交于点P.
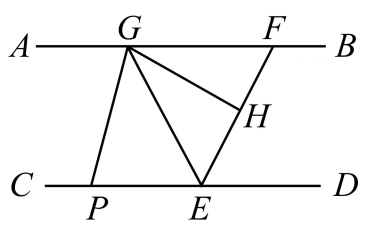 (1)、求证:;(2)、设 , 求的度数,
(1)、求证:;(2)、设 , 求的度数, -
3、 某校计划购买A、B两种型号的机器人,已知购买1台A型机器人和2台B型机器人共需11万元,购买2台A型机器人和3台B型机器人共需19万元.(1)、每台A型机器人和B型机器人的售价分别为多少万元?(2)、若该校计划购买A、B两种型号机器人共25台,且购买A型机器人的总费用不超过购买B型机器人的总费用,则该校最多可购买A型机器人多少台?
-
4、 如图,在平面直角坐标系中,点 , , , 将线段平移得到线段 , 点A与点C是对应点.
 (1)、点D的坐标是;(2)、若点P为y轴上一点,且三角形的面积与三角形的面积相等,求点P的坐标.
(1)、点D的坐标是;(2)、若点P为y轴上一点,且三角形的面积与三角形的面积相等,求点P的坐标. -
5、 完成下面的证明并填上推理根据.
如图所示,点C,F分别为三角形ABE的边BE,AE上的一点,点D在线段CF的延长线上,且 , , , 求证: .
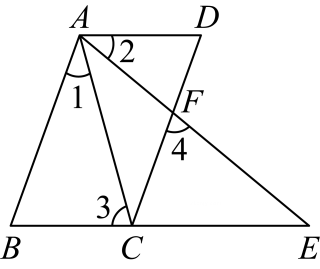
证明:∵(),
∴().
∵(已知),
∴().
∵(已知),
∴(),
即 ,
∴(等式的基本事实),
∴().
-
6、 为了解全校学生参与家务劳动的情况,某学校开展了“一周参与家务劳动时间”的问卷调查,根据收集到的数据,将劳动时间(单位:)分为(),(),(),()四组进行统计,并绘制了如图所示的不完整的条形图和扇形图.
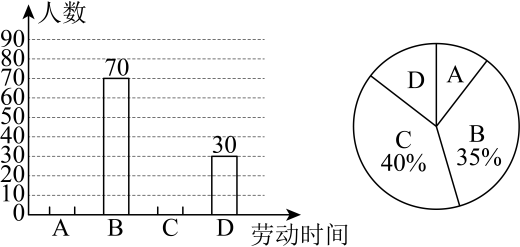 (1)、这次一共调查了多少名学生?(2)、请把条形统计图补充完整;(3)、若这所学校共有1500名学生,根据以上调查结果,估计这所学校学生中一周参与家务劳动时间不少于的学生大约有多少人.
(1)、这次一共调查了多少名学生?(2)、请把条形统计图补充完整;(3)、若这所学校共有1500名学生,根据以上调查结果,估计这所学校学生中一周参与家务劳动时间不少于的学生大约有多少人. -
7、 利用数轴求不等式组的解集.
-
8、 解方程组:
-
9、 计算: .
-
10、 如图,在三角形中, , 将三角形沿着方向向右平移个单位得到三角形 , 点在线段上,若 , , 与相交于点 .
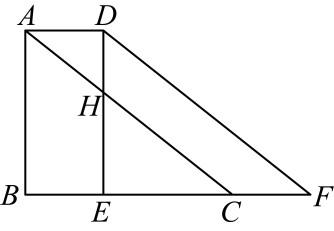 (1)、线段的长为;(2)、四边形的面积为 .
(1)、线段的长为;(2)、四边形的面积为 . -
11、 为了研究气温对冷饮销售的影响,一家饮品店经过一段时间的统计,得到一组卖出冷饮杯数与当天的最高气温的数据,为了更加清楚地看出冷饮杯数与最高气温之间的关系,用横轴表示最高气温,用纵轴表示冷饮杯数,描出各组数据对应的点,如图所示.利用趋势图可以估计当一天的最高气温为时,饮品店一天可卖出的冷饮杯数约为杯.

-
12、 比较大小: 2(填“>”或“=”或“<” ).
-
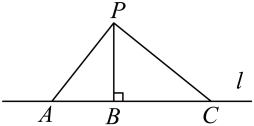
13、 如图,P是直线l外一点,点A,B,C在直线l上, , 垂足为B, , , , 则点P到直线l的距离是 .
-
14、 如图,在平面直角坐标系中,点 , 点 , 则 .

-
15、 若为方程的一组解,则点不可能在第( )象限.A、一 B、二 C、三 D、四
-
16、 下列命题中,是真命题的是( )A、有理数和数轴上的点是一一对应的 B、过直线外一点有且只有一条直线与已知直线垂直 C、过直线外一点有且只有一条直线与已知直线平行 D、两条直线被第三条直线所截,内错角相等
-
17、 若 , 则下列说法正确的是( )A、 B、 C、 D、
-
18、 《算法统宗》是我国古代著名的数学典籍,其中有一道题:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空,问房几间?客几何?意思是:李三公家开店,来了一批客人,一个房间住7位客人则多出7位客人,一个房间住9位客人则多出1个房间,问李三公家的店有多少个房间?来了多少位客人?设李三公家的店有个房间,来了位客人,则可以列出的方程组为( )A、 B、 C、 D、
-
19、 如图, , 下列说法正确的是( )
 A、 B、 C、 D、平分
A、 B、 C、 D、平分 -
20、 为了了解全校2500名学生参与家务劳动的情况,随机抽取200名学生进行了“一周参与家务劳动时间”的问卷调查.在收集到的数据中,一周参与家务劳动时间不少于的学生人数为70人.占抽查学生人数的35%.这项调查的样本容量是( )A、2500 B、200 C、70 D、