相关试卷

1、已知□ABCD。

(1)、如图1，E是AD上一点，以点C为圆心，AE的长为半径作弧，交BC于点F，连结AF，CE。求证：四边形AFCE是平行四边形。

(2)、图1中□AFCE的四个顶点在□ABCD的边上，这样的四边形叫□ABCD的内接四边形。在图2中用直尺和圆规作一个□ABCD的内接菱形（保留作图痕迹）。

查看解析
2、为了解七（1）班和八（1）班同学的课外阅读情况，每个班随机抽取10名同学进行问卷调查，并对平均每周阅读时长（单位：小时）的数据进行整理和分析。
整理数据：
七（1）
4
6
6
7
7
7
7
8
8
10
八（1）
5
5
6
7
7
8
8
8
8
8
分析数据：
班级
平均数
中位数
众数
方差
七（1）
7
7
7
2.2
八（1）
7
a
b
c
根据以上信息解决下列问题：

(1)、填空：a=；b=；c=.

(2)、甲同学说“我平均每周阅读7.2小时，位于班级中上水平”，你认为甲的说法对吗？请说明理由。

查看解析
3、以下是小数同学解方程x（x-1）=2（x-1）的过程。
解：方程两边同除以（x-1），得x=2。
根据小数的解题过程，回答下列问题：

(1)、小π同学认为小数的解题过程有错，请帮小数找出错误原因。

(2)、请你写出正确的解答过程。

查看解析
4、计算： $(\sqrt{2})^{2} - \sqrt{8} + | \sqrt{2} - 1 |$

查看解析

5、如图1是某种简易房屋，它由顶角为120°的等腰三角形和矩形组成，在整体运输时需用钢丝绳进行加固，示意图如图2所示。MN是一条两端点位置和长度均可调节的钢丝绳，点M在EC上，点N在AB上，在调整钢丝绳端点位置时，其长度也随之改变，但需始终保持EM=BN。若DE=EC=BC=4米，则钢丝绳MN长度的最小值为米。

嗨，你好！我是小数，对于此题，我是这样思考的：通过构造□MNBP，把MN转化为BP，从而把双动点问题转化为单动点问题，这样就很容易解决问题了。你试试看!

查看解析

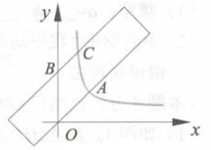
6、将一把直尺如图所示放置在平面直角坐标系中，过原点的一边与x轴的夹角为45°，另一边交y轴于点B，与双曲线交于点A和C。若点A的横坐标为1，点B的纵坐标为2，则点C的坐标为。

查看解析
7、写一个二次项系数为1，两根分别为-2和3的一元二次方程：.

查看解析
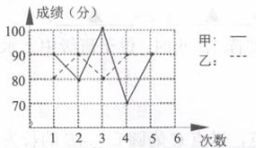
8、甲、乙两人5次数学成绩如图所示，其中成绩较稳定的是.

查看解析
9、如图，在一束平行光线中插入一张对边平行的纸板。如果光线与纸板右下方所成的∠1为80°，那么光线与纸板左上方所成的∠2的度数为°。

查看解析
10、在四边形ABCD中，AC⊥BD，E，F分别是AD和BC的中点。若AC=6，BD=8，则EF为（）

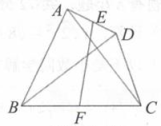A、5 B、6 C、8 D、10

查看解析
11、点 $A (x_{1}, y_{1})$ ， $B (x_{2}, y_{2})$ 在反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象上，则下列结论错误的是（）

A、若 $x_{1} < x_{2} < 0$ ，则 $y_{1} - y_{2} > 0$ B、若 $0 < x_{1} < x_{2}$ ，则 $y_{1} - y_{2} > 0$ C、若 $x_{1} < 0 < x_{2}$ ，则 $y_{1} - y_{2} < 0$ D、若 $x_{1} < 0 < x_{2}$ ，则 $y_{1} + y_{2} > 0$

查看解析
12、如图，在□ABCD中，E，F分别是AD和BC的中点，P是AB上的一个动点，从点A运动到点B。在点P的运动过程中，APED与APFC的面积之和（）

A、不变 B、变小 C、变大 D、先变大再变小

查看解析
13、俗语有云：“一天不练手脚慢，两天不练丢一半。”其意思是知识和技艺学习后，如果不及时复习，那么很容易被遗忘。假设每天“遗忘”的百分比为x，根据“两天不练丢一半”，可列方程为（）

A、（1+x）²=50% B、（1-x）²=50% C、1-2x=50% D、（1-x）（1+x）=50%

查看解析
14、用反证法证明命题“在△ABC中，若∠B>∠C，则AC>AB。”，应假设（）

A、AC>AB B、AC≤AB C、∠B>∠C D、∠B≤∠C

查看解析
15、用直接开平方法解下列一元二次方程，其中无解的方程为（）

A、 $x^{2} = 0$ B、 $x^{2} - 2 = 0$ C、 $- x^{2} + 2 = 0$ D、 $x^{2} + 2 = 0$

查看解析
16、某校设置了游泳课外兴趣小组，为了统一服装，对同学们喜欢什么颜色的泳衣进行了调查统计，老师应该关注的数据是（）

A、平均数 B、中位数 C、众数 D、以上都不对

查看解析
17、下列二次根式中，最简二次根式是（）

A、 $\sqrt{0.5}$ B、 $\sqrt{\frac{1}{5}}$ C、 $\sqrt{5}$ D、 $\sqrt{50}$

查看解析
18、下列分子结构图中，是中心对称图形的是（）

A、苯分子结构图 B、乙烯分子结构图 C、丙烯分子结构图 D、丙烷分子结构图

查看解析
19、若 $\sqrt{a - 3}$ 在实数范围内有意义，则整数a可以是（）

A、0 B、1 C、2 D、3

查看解析
20、如图1，在矩形ABCD中，AB=4 $\sqrt{3}$ ， BC=4，对角线AC，BD交于点O，E为OC上一点（不与点O，C重合），延长BE到点F，使BE=EF，交边CD于点P，连结DF.

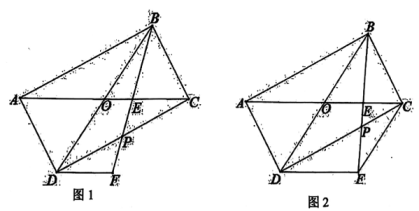(1)、求证：DF∥AC.

(2)、当CE=2OE时，求BF的长.

(3)、如图2，连结CF，当∠DCF等于△ABC的某个内角时，求所有符合条件的四边形DOEF的面积.

查看解析

上一页 680 681 682 683 684 下一页跳转

班级	平均数	中位数	众数	方差
七（1）	7	7	7	2.2
八（1）	7	a	b	c