-
1、如图,在菱形ABCD中,∠A=60°AB=4,E是AD边上的动点,作∠BEF=60咬CD于点F,在AB上取点G使AG=AE,连结EG.
 (1)、求∠EGB的度数:(2)、求证:EF=BE:(3)、若P是EF的中点,当AE为何值时,△EGP是等腰三角形.
(1)、求∠EGB的度数:(2)、求证:EF=BE:(3)、若P是EF的中点,当AE为何值时,△EGP是等腰三角形. -
2、如图1,在平面直角坐标系xOy中,点F(2,2),过函数常数k>0)图象上一点A( , a)作y轴的平行线交直线l:y=-x+2于点C,且AC=AF.
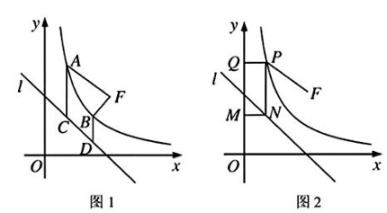 (1)、求a的值,并写出函数的解析式;(2)、过函数图象上任意一点B,作y轴的平行线交直线l于点D,是否总有BD=BF成立?并说明理由;(3)、如图2,若P是函数图象上的动点,过点P作x轴的垂线交直线l于点N,分别过点P、N作y轴的垂线交y轴于点Q、M,问:是否存在点P,使得矩形PQMN的周长取得最小值?若存在,请求出此时点P的坐标及矩形PQMN的周长;若不存在,请说明理由.
(1)、求a的值,并写出函数的解析式;(2)、过函数图象上任意一点B,作y轴的平行线交直线l于点D,是否总有BD=BF成立?并说明理由;(3)、如图2,若P是函数图象上的动点,过点P作x轴的垂线交直线l于点N,分别过点P、N作y轴的垂线交y轴于点Q、M,问:是否存在点P,使得矩形PQMN的周长取得最小值?若存在,请求出此时点P的坐标及矩形PQMN的周长;若不存在,请说明理由. -
3、已知方程的两个根是 , , 那么 , , 反过来,如果 , , 那么以 , 为两根的一元二次方程是.请根据以上结论,解决下列问题:(1)、已知关于x的方程 , 求出一个一元二次方程,使它的两根分别是已知方程两根的倒数.(2)、已知a,b满足 , , 求的值.(3)、已知a,b,c均为实数,且 , , 求正数c的最小值.
-
4、如图,在平面直角坐标系中,已知直线分别交反比例函数和在第一象限的图于点A,B,过点B作BD⊥x轴于点D,交的图象于点C,连接AC.若是等腰三角形,则k的值是.

-
5、如图所示,以的斜边BC为一边在的同侧作正方形BCEF,设正方形的中心为O,连AO,如果 , , 那么.

-
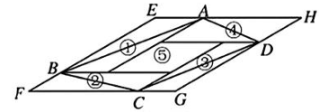
6、如图,①②③④⑤五个平行四边形拼成一个含30内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2 , 四边形ABCD面积是11cm2 , 则①②③④四个平行四边形周长的总和为.
-
7、已知a是方程的一个根,则的值为.
-
8、如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连结AE.若AD平分∠OAE,反比例函数y=(k>0,x>0)的图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为( )
 A、6 B、12 C、18 D、24
A、6 B、12 C、18 D、24 -
9、如图,在锐角三角形ABC中,点D,E,F分别是边BC,CA,AB的中点,从每边中点分别作其余两边的垂线,这六条垂线围成六边形DPEQFR,设六边形DPEQFR的面积为 , 的面积为S,则( )
 A、3:5 B、2:3 C、1:2 D、1:3
A、3:5 B、2:3 C、1:2 D、1:3 -
10、如图,矩形ABCD中,E为边AD上一点(不为端点),交AC于点F,要求的面积,只需知道下列哪个三角形的面积即可( )
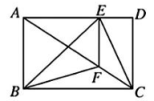 A、 B、 C、 D、
A、 B、 C、 D、 -
11、当m,n是实数且满足时,就称点Q(m,)为“奇异点”,已知点A、点B是“奇异点”且都在反比例函数的图象上,点O是平面直角坐标系原点,则的面积为( )A、1 B、 C、2 D、
-
12、如图,在□ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=4,将△ABC沿直线AC翻折180后与原图形在同一平面内,若点B的落点记为B' , 则DB'的长为( )
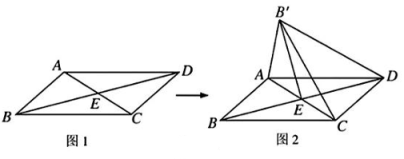 A、 B、 C、 D、
A、 B、 C、 D、 -
13、某工厂第二季度的产值比第一季度的产值增长了x%,第三季度的产值又比第二季度的产值增长了x%,则第三季度的产值比第一季度增长了( )A、2x% B、1+2x% C、(1+x%)·x% D、(2+x%)·x%
-
14、已知 , , 则用a,b表示为( )A、 B、 C、 D、
-
15、如图,在四边形 中, 于 于 为 的垂心,求证: 三点共线.

-
16、是否存在正整数 满足 . 若存在请求出值; 若不存在请说明理由.
-
17、已知 ,满足 .(1)、 求 ;(2)、对于任意整数 ,使得 恒成立,求 的最大值.
-
18、现有 三个正整数, 均为正整数,求 的最大值与最小值之和.
-
19、如图,在 中, , 则 .

-
20、已知 ,则 .