-
1、点A，B在半径为2的上， ， ， 垂足为C．绕点C顺时针旋转，分别交于点M，N（均位于直线上方），连接 ．
（1）如图1，当时，；
（2）如图2，当时， ．
-
2、给出一组数据：23，22，25，23，27，25，23，则这组数据的中位数是；方差是（精确到0.1）．
-
3、2024年6月6日，嫦娥六号在距离地球约384000千米外上演“太空牵手”，完成月球轨道的交会对接，数据384000用科学记数法表示为 ．
-
4、如图，在中， ， 相交于点 ， 过点作 ， ， ， ． 记长为 ， 长为 ． 当 ， 的值发生变化时，下列代数式的值不变的是（ ）
A、 B、 C、 D、 -
5、如图，在四边形中，分别与扇形相切于点 ． 若 ， 则的长为（ ）
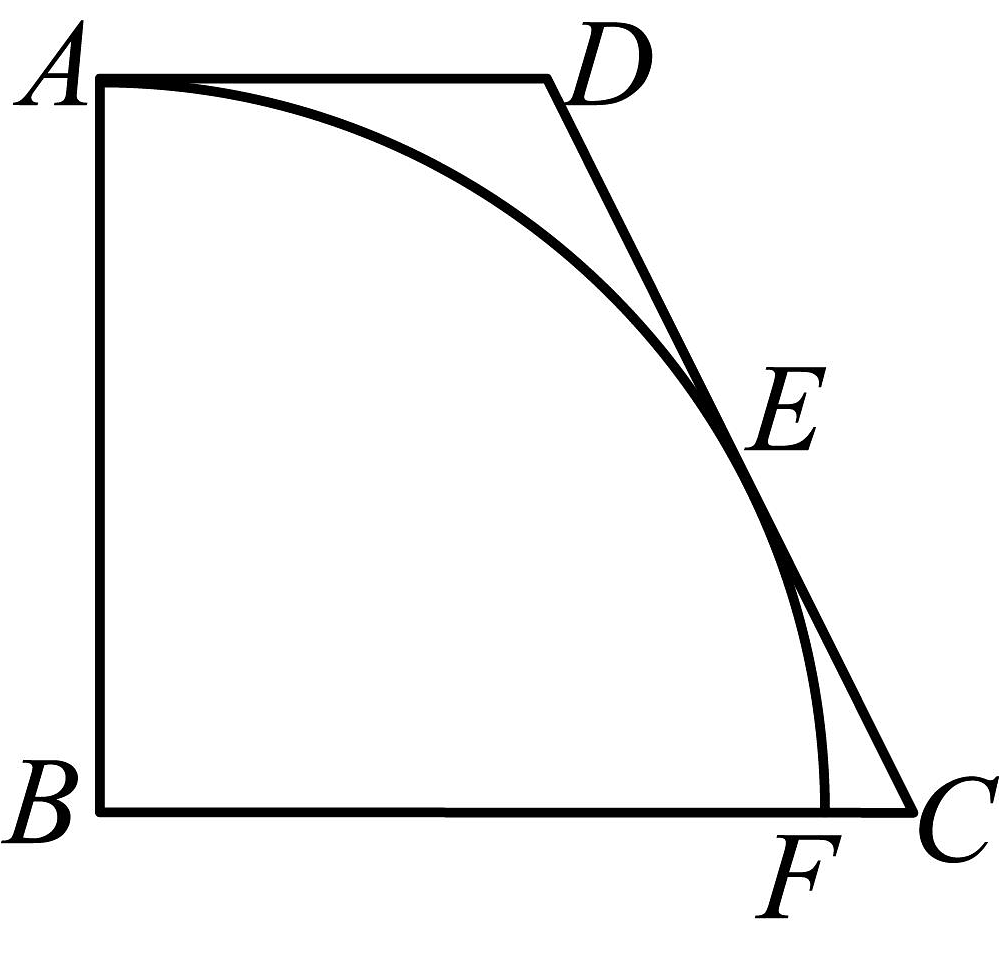A、8 B、 C、 D、9 -
6、计算的结果是（ ）A、 B、 C、 D、
-
7、已知：如图，线段AC和BD相交于点G，连接AB，CD，E是CD上一点，F是DG上一点，FE∥CG，且∠1=∠A．
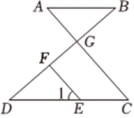(1)、求证：AB∥DC；(2)、若∠B=30°，∠1=62°，求∠EFG的度数． -
8、某校组织全校3000名学生进行了“新冠”防疫知识竞赛．为了解成绩的分布情况，随机抽取了部分学生的成绩（得分取整数，满分为100分），并绘制了如图所示的频数分布表和频数分布直方图．
抽取部分学生成绩的频率分布表
成绩分组
频数
频率
50.5～60.5
20
0.05
60.5～70.5
a
0.15
70.5～80.5
76
b
80.5～90.5
104
0.26
90.5～100.5
140
c
合计
d
1
根据所给信息，回答下列问题：
(1)、根据频数分布表填空：a= ， b+c= ，d= ；(2)、补全频数分布直方图；(3)、学校将对成绩在90.5～100.5分之间的学生进行奖励，估算出全校获奖学生的人数． -
9、计算.
-
10、已知关于x，y的方程组的解为非负数，m-2n=3，z=2m+n，且n＜0，则z的取值范围是 ．
-
11、如图，直线a、b被直线c所截，若a∥b，∠1=120°，∠2=56°，则∠3= ．
-
12、如图，直线AB，CD相交于点O，OE⊥AB，OF平分∠EOD，若∠AOC=40°，则∠FOB= °．
-
13、 设（a，b）表示a，b两数中取较小的一个，[a，b]表示a，b两数中取较大的一个，则（-3，[-6，-9]）÷[（-3，-16），-9]= ．
-
14、若关于x，y的二元一次方程组 中，x的值为负数，y的值为正数，则m的取值范围是 ．
-
15、已知方程是二元一次方程，则m+n= ．
-
16、将一副三角板按如图放置，则下列结论①∠1=∠3；②如果∠1=30°，则有AC∥DE；③如果∠2=45°，则有BC∥AD；④如果∠4=∠C，必有∠2=30°，其中正确的有（ ）
A、①②③ B、①②④ C、①③④ D、①②③④ -
17、某电影院1号厅正在放映电影《哪吒之魔童闹海》，甲、乙两名工作人员根据1号厅的观影人数，说法如下：
甲：“观影人数不超过90人．”
乙：“观影人数不足100人．”
已知甲的说法错误，乙的说法正确，则在1号厅的观影人数可能为（ ）
A、90 B、96 C、100 D、101 -
18、 如图是路政工程车的工作示意图，工作篮底部与支撑平台平行．若∠1=30°，∠2=60°，则∠3的度数为（ ）
A、130° B、140° C、150° D、160° -
19、《九章算术》是中国古代著名的数学专著，书里记载一道这样的题：“今有漆三得油四，油四和漆五．今有漆三斗，欲令分以易油，还自和余漆．问出漆、得油、和漆各几何？”题目译文是：若有三份漆可换得4份油，用4份油可调5份漆．今有漆3斗，要分出一部分来换油，换回油后用以调所余之漆．问拿出换油的漆、换得的油、留下用于调和用的漆各是多少？若设拿出换油的漆为x，换得的油为y，根据题意可列方程组为（ ）A、 B、 C、 D、
-
20、在平面直角坐标系中，点A的坐标为（2，1），将点A向右平移2个单位长度得到点A'，则点A'的坐标为（ ）A、（2，-1） B、（2，3） C、（4，1） D、（0，1）